acm数论之旅--组合数(转载)
ACM数论之旅8---组合数(组合大法好(,,• ₃ •,,) )
一道组合数与全错排的公式。
组合数并不陌生(´・ω・`)
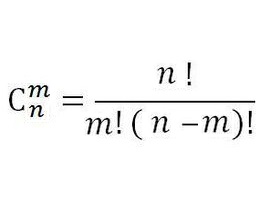

我们都学过组合数
会求组合数吗
一般我们用杨辉三角性质
杨辉三角上的每一个数字都等于它的左上方和右上方的和(除了边界)

第n行,第m个就是,就是C(n, m) (从0开始)
电脑上我们就开一个数组保存,像这样
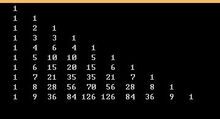
用递推求
1 #include<cstdio>
2 const int N = 2000 + 5;
3 const int MOD = (int)1e9 + 7;
4 int comb[N][N];//comb[n][m]就是C(n,m)
5 void init(){
6 for(int i = 0; i < N; i ++){
7 comb[i][0] = comb[i][i] = 1;
8 for(int j = 1; j < i; j ++){
9 comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
10 comb[i][j] %= MOD;
11 }
12 }
13 }
14 int main(){
15 init();
16 }
https://ac.nowcoder.com/acm/contest/881#question E题,另外一种求组合数。
#include<bits/stdc++.h> #define ll long long #define M (ll)(1e9+7) using namespace std; ll CM[4001]={1}; ll Pow(ll a,ll b){ //快速幂 a%=M; ll ans = 1; for(;b;b>>=1) { if(b&1) ans = (ans*a)%M; a = (a*a)%M; } return ans; } ll Quk(ll a,ll b){ //快速乘 a%=M; ll ans = 0; for(;b;b>>=1) { if(b&1) ans = (ans+a)%M; a = (a+a)%M; } return ans; } ll C(ll m,ll n){ //n>=m return Quk(Quk(CM[n],Pow(CM[n-m],M-2)),Pow(CM[m],M-2))%M; } ll A(ll m,ll n){ //n>=m return Quk(CM[n],Pow(CM[n-m],M-2))%M; } int main() { ll a,b; for(int i=1;i<4001;i++) CM[i]=Quk(CM[i-1],i); while(cin>>a>>b) { ll ans=C(a+b,2*(a+b)); if(a) ans-=C(a-1,2*(a+b)); if(b) ans-=C(b-1,2*(a+b)); cout<<(ans+2*M)%M<<endl; } return 0; }
需要mod是质数
#include<bits/stdc++.h> using namespace std; #define INF 0x3fffffff #define maxn 100005 typedef long long ll; ll n,m,k,t; const ll mod = 1e9+7; ll fac[maxn]; ll inv[maxn]; ll qpow(ll a, ll b) { ll r = 1, t = a; while (b) { if (b & 1)r = (r*t) % mod; b >>= 1;t = (t*t) % mod; } return r; } void init() { fac[0] = 1; for (int i = 1;i <= mmax;i++) fac[i] = fac[i - 1] * 1ll * i%mod; inv[mmax] = qpow(fac[mmax], mod - 2); for (int i = mmax - 1;~i;i--) inv[i] = inv[i + 1] * 1ll * (i + 1) % mod; } ll C(ll n, ll m) { if (m>n) return 0; if (m == n || m == 0) return 1; return fac[n] * 1ll * inv[n - m] % mod*inv[m] % mod; } int main(){ init(); while(~scanf("%lld%lld",&n,&m)) printf("%lld\n",(C(2*m+2*n,n+m)+mod-(C(2*m+2*n,n-1)+C(2*m+2*n,m-1))%mod)%mod); }
(PS:大部分题目都要求求余,而且大部分都是对1e9+7这个数求余)
这种方法的复杂度是O(n^2),有没有O(n)的做法,当然有(´・ω・`)
因为大部分题都有求余,所以我们大可利用逆元的原理(没求余的题目,其实你也可以把MOD自己开的大一点,这样一样可以用逆元做)
根据这个公式
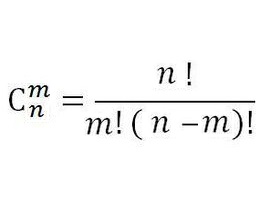
我们需要求阶乘和逆元阶乘
我们就用1e9+7来求余吧
long long F[100010]; void init(long long p) { F[0] = 1; for(int i = 1;i <= p;i++) F[i] = F[i-1]*i % (1000000007); } long long inv(long long a,long long m) { if(a == 1)return 1; return inv(m%a,m)*(m-m/a)%m; } long long Lucas(long long n,long long m,long long p) { long long ans = 1; while(n&&m) { long long a = n%p; long long b = m%p; if(a < b)return 0; ans = ans*F[a]%p*inv(F[b]*F[a-b]%p,p)%p; n /= p; m /= p; } return ans; }
代码如下:
1 #include<cstdio>
2 const int N = 200000 + 5;
3 const int MOD = (int)1e9 + 7;
4 int F[N], Finv[N], inv[N];//F是阶乘,Finv是逆元的阶乘
5 void init(){
6 inv[1] = 1;
7 for(int i = 2; i < N; i ++){
8 inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
9 }
10 F[0] = Finv[0] = 1;
11 for(int i = 1; i < N; i ++){
12 F[i] = F[i-1] * 1ll * i % MOD;
13 Finv[i] = Finv[i-1] * 1ll * inv[i] % MOD;
14 }
15 }
16 int comb(int n, int m){//comb(n, m)就是C(n, m)
17 if(m < 0 || m > n) return 0;
18 return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
19 }
20 int main(){
21 init();
22 }




