最短路问题
第一种是不优化的dijiesitela算法,用邻接矩阵输入。
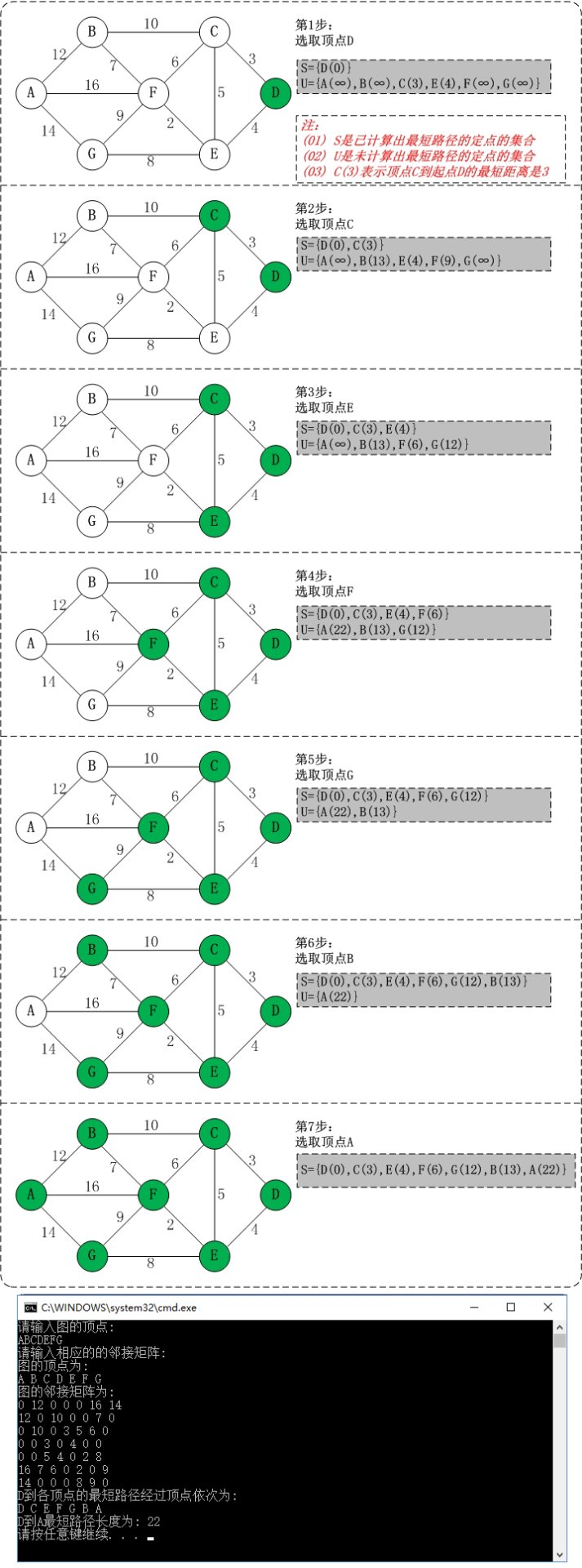
#include<cstdio> const int maxm = 105; const int INF = 1e5 + 5; #include<algorithm> #include<cstring> #include<queue> using namespace std; int mapp[maxm][maxm]; bool vis[maxm]; int dp[maxm]; char ch[maxm]; int v; queue<int> q; void Dijstela(int star, int endd){ int minn; int index; memset(vis, 0, sizeof(vis)); vis[star] = 1; dp[star] = 0; for(int i = 0; i < v; i++){ dp[i] = mapp[star][i]; } for(int i = 0; i < v - 1; i++){ minn = INF; for(int j = 0; j < v; j++) { if(dp[j] < minn && !vis[j])找到最小的 { index = j; minn = dp[j]; } } if(minn == INF) break; //说明这些点的集合与其他点之间没有联通的地方。 q.push(index); vis[index] = 1; for(int j = 0; j < v; j++)更新每个点的最短路径 { if(dp[index] + mapp[index][j] < dp[j] && !vis[j]) dp[j] = dp[index] + mapp[index][j]; } } } int main(){ scanf("%s", ch); memset(dp, 0, sizeof(dp)); v = strlen(ch); for(int i = 0; i < v; i++){ if(i == v - 1) printf("%c\n", ch[i]); else printf("%c ", ch[i]); } for(int i = 0; i < v; i++){ for(int j = 0; j < v; j++){ scanf("%d", &mapp[i][j]); } } for(int i = 0; i < v; i++){ for(int j = 0; j < v; j++){ mapp[i][j] = mapp[i][j] == 0 ? INF : mapp[i][j]; } } q.push(3); Dijstela(3, 0); printf("%d\n", dp[0] == INF ? -1 : dp[0]); while(!q.empty()){ int yuan = q.front(); q.pop(); printf("%c ", yuan + 'A'); } return 0; }
https://blog.csdn.net/qq_38367681/article/details/81178337
https://blog.csdn.net/wang_123_zy/article/details/82497369
前向星建图
floyd (弗洛伊德算法) Dijkstra(迪杰斯特拉算法) bellman-ford(贝尔曼夫德算法) spfa
空间复杂度 O(N²) O(M) O(M) O(M)
时间复杂度 O(N³) O((m+n)logN) O(MN) 最坏也是O(NM)
适用情况 稠密图和顶点关系密切 稠密图和顶点关系密切 稀疏图和边关系密切 稀疏图和边关系密切
负权 可以 不能 可以 可以
有负权边时可否处理 可以 不能 可以 可以
判断是否存在负权回路 不能 不能 可以 可以
其中N表示点数,M表示边数
Floyd 算法虽然总体上时间复杂度较高,但可以处理带负权边的图(但不能有负权回路),并且均摊到每一点对上,在所有的算法中还是属于比较优秀的算法。另外,floyd算法较小的编码复杂度也是一大优势,所以,如果要求的是所有点对间的最短路径,或者如果数据范围较小,则floyd算法比较合适。
Dijkstra算法最大的弊端就是他无法处理带有负权边以及负权回路的图,但是Dijkstra算法具有良好的可扩展性,扩展后可以适应很多问题。另外用堆优化的Dijkstra算法的时间复杂度可以达到O(M log N)。当边有负权,甚至存在负权回路时,需要使用Bellman-ford 算法或者队列优化的Bellman-ford算法,因此我们选择最短路径法时,根据实际的需求和每一种算法的特性,选择合适的算法来使用
Dijkstra
dijkstra算法本质上算是贪心的思想,每次在剩余节点中找到离起点最近的节点放到队列中,并用来更新剩下的节点的距离,再将它标记上表示已经找到到它的最短路径,以后不用更新它了。这样做的原因是到一个节点的最短路径必然会经过比它离起点更近的节点,而如果一个节点的当前距离值比任何剩余节点都小,那么当前的距离值一定是最小的。(剩余节点的距离值只能用当前剩余节点来更新,因为求出了最短路的节点之前已经更新过了)
dijkstra就是这样不断从剩余节点中拿出一个可以确定最短路径的节点最终求得从起点到每个节点的最短距离。
Bellman-Ford
bellman-ford算法进行n-1次更新(一次更新是指用所有节点进行一次松弛操作)来找到到所有节点的单源最短路。bellman-ford算法和dijkstra其实有点相似,该算法能够保证每更新一次都能确定一个节点的最短路,但与dijkstra不同的是,并不知道是那个节点的最短路被确定了,只是知道比上次多确定一个,这样进行n-1次更新后所有节点的最短路都确定了(源点的距离本来就是确定的)。
现在来说明为什么每次更新都能多找到一个能确定最短路的节点:
1.将所有节点分为两类:已知最短距离的节点和剩余节点。
2.这两类节点满足这样的性质:已知最短距离的节点的最短距离值都比剩余节点的最短路值小。(这一点也和dijkstra一样)
3.有了上面两点说明,易知到剩余节点的路径一定会经过已知节点
4.而从已知节点连到剩余节点的所有边中的最小的那个边,这条边所更新后的剩余节点就一定是确定的最短距离,从而就多找到了一个能确定最短距离的节点,不用知道它到底是哪个节点。
bellman-ford的一个优势是可以用来判断是否存在负环,在不存在负环的情况下,进行了n-1次所有边的更新操作后每个节点的最短距离都确定了,再用所有边去更新一次不会改变结果。而如果存在负环,最后再更新一次会改变结果。原因是之前是假定了起点的最短距离是确定的并且是最短的,而又负环的情况下这个假设不再成立。
Spfa
spfa可以看成是bellman-ford的队列优化版本,正如在前面讲到的,bellman每一轮用所有边来进行松弛操作可以多确定一个点的最短路径,但是用每次都把所有边拿来松弛太浪费了,不难发现,只有那些已经确定了最短路径的点所连出去的边才是有效的,因为新确定的点一定要先通过已知(最短路径的)节点。
所以我们只需要把已知节点连出去的边用来松弛就行了,但是问题是我们并不知道哪些点是已知节点,不过我们可以放宽一下条件,找哪些可能是已知节点的点,也就是之前松弛后更新的点,已知节点必然在这些点中。
所以spfa的做法就是把每次更新了的点放到队列中记录下来。
在实现上,bellman-ford可以用边集数组或链式前向星来实现。
而spfa则只能用链式前向星实现。
在效率上,当图很稠密的时候spfa就退化成和bellman -ford差不多了,因为对于入队的每个节点都要和很多节点去进行松弛操作
spfa的堆优化与dijstela的堆优化
https://blog.csdn.net/u012915516/article/details/23136549
//spfa算法 #include<cstdio> #include<cstring> #include<algorithm> #include<vector> #include<queue> using namespace std; const int inf = 1e9 + 7; struct edge { int from,to,cost; }; const int maxm = 105; vector <edge> ve[maxm]; typedef pair<int, int> pii; edge e[maxm * maxm]; int d[maxm], used[maxm];//used数组记录是否已经松弛过 int n, m; void spfa(int x) { memset(used, 0, sizeof*used); for(int i = 1; i <= n; i++) { d[i] = inf; } queue<int> q; d[x] = 0; used[x] = 1; q.push(x); while(!q.empty()) { int id = q.front(); used[id] = 0; for(int i = 0; i < ve[id].size(); i++) { edge t = ve[id][i]; if(d[t.to] > d[id]+t.cost) { d[t.to] = d[id] + t.cost; if(!used[t.to]) { used[t.to] = 1; q.push(t.to); //if(++cnt[e.to] > n) //return true; //这是判负环的代码,cnt初始化为零。 } } } q.pop(); } } int main() { while(~scanf("%d%d", &n, &m)) { if(n == 0 && m == 0) break; for(int i = 1; i <= n; i++) { ve[i].clear(); } for(int i = 1; i <= m; i++) { scanf("%d%d%d", &e[i].from, &e[i].to, &e[i].cost); ve[ e[i].from ].push_back(e[i]); swap(e[i].from, e[i].to); ve[ e[i].from ].push_back(e[i]); } spfa(1); printf("%d\n", d[n]); } return 0; }
迪杰斯特拉算法 #include<cstdio> #include<cstring> #include<algorithm> #include<vector> #include<queue> using namespace std; const int inf = 1e9 + 7; struct edge { int from,to,cost; };//from好像可以去掉 const int maxm = 105; vector <edge> ve[maxm]; typedef pair<int, int> pii; edge e[maxm * maxm]; int d[maxm]; priority_queue<pii, vector<pii>, greater<pii>>q; int n, m; void dijkstra(int a) { while(!q.empty()) q.pop(); for(int i = 1; i <= n; i++) d[i] = inf; d[a] = 0; q.push(pii(0, a)); while(!q.empty()) { pii p = q.top(); q.pop(); int v = p.second; if(d[v] < p.first)//已经松弛过了就不用进去了 continue; for(int i = 0; i < ve[v].size(); i++) { edge e = ve[v][i]; if(d[e.to] > d[v] + e.cost) { d[e.to] = d[v] + e.cost; q.push(pii(d[e.to], e.to)); } } } } int main() { while(~scanf("%d%d", &n, &m)) { if(n == 0 && m == 0) break; for(int i = 1; i <= n; i++) { ve[i].clear(); } for(int i = 1; i <= m; i++) { scanf("%d%d%d", &e[i].from, &e[i].to, &e[i].cost); ve[ e[i].from ].push_back(e[i]); swap(e[i].from, e[i].to); ve[ e[i].from ].push_back(e[i]); } dijkstra(1); printf("%d\n", d[n]); } return 0; }
给你n个点,m条无向边,每条边都有长度d和花费p,给你起点s终点t,要求输出起点到终点的最短距离及其花费,如果最短距离有多条路线,则输出花费最少的。
#include<cstdio> #include<cstring> #include<algorithm> #include<vector> #include<queue> using namespace std; const int inf = 1e9 + 7; struct edge{int from,to,dis,cost;}; const int maxm = 1005; vector <edge> ve[maxm]; typedef pair<int, int> pii; edge e[maxm * maxm]; int d[maxm], cost[maxm]; priority_queue<pii, vector<pii>, greater<pii>>q; int n, m; void dijkstra(int a) { while(!q.empty()) q.pop(); for(int i = 1; i <= n; i++) { d[i] = inf; cost[i] = inf; } d[a] = 0; cost[a] = 0; q.push(pii(0, a)); while(!q.empty()) { pii p = q.top(); q.pop(); int v = p.second; if(d[v] < p.first) continue; for(int i = 0; i < ve[v].size(); i++) { edge e = ve[v][i]; if(d[e.to] > d[v] + e.dis) { d[e.to] = d[v] + e.dis; cost[e.to] = cost[v] + e.cost;//////////////加的 q.push(pii(d[e.to], e.to)); } else if(d[e.to] == d[v] + e.dis) {/////////////// cost[e.to] = min(cost[e.to], cost[v] + e.cost);////////////////如果最短路距离相等就要比较花费 } } } } int l, r; int main() { while(~scanf("%d%d", &n, &m)) { if(n == 0 && m == 0) break; for(int i = 1; i <= n; i++) { ve[i].clear(); } for(int i = 1; i <= m; i++) { scanf("%d%d%d%d", &e[i].from, &e[i].to, &e[i].dis, &e[i].cost); ve[ e[i].from ].push_back(e[i]); swap(e[i].from, e[i].to); ve[ e[i].from ].push_back(e[i]); } scanf("%d%d", &l, &r); dijkstra(l); printf("%d %d\n", d[r], cost[r]); } return 0; }
floyed算法https://vjudge.net/contest/280903#problem/N就是求汇率,两两之间,单向的,看那个最后可以赚。 HDU1217
#include<cstdio> #include<algorithm> #include<cstring> #include<map> using namespace std; const int maxm = 32; map<string, int> mapp; double cost[maxm][maxm], val; int n, m; char ch[100], st[100], en[100]; int ant = 0; int main() { while(~scanf("%d", &n)) { if(n == 0) break; for(int i = 0; i < n; i++) { scanf("%s", ch); mapp[ch] = i; } for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { if(i == j) cost[i][j] = 1.0; else cost[i][j] = 0; } } scanf("%d", &m); for(int i = 0; i < m; i++) { scanf("%s%lf%s", st, &val, en); cost[ mapp[st] ][ mapp[en] ] = val; } int flag = 0; for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { for(int k =0; k < n; k++) { if(cost[j][k] < cost[j][i] * cost[i][k]) { cost[j][k] = cost[j][i] * cost[i][k]; } if(j == k && cost[j][k] > 1.0) { flag = 1; break; } } if(flag) break; } if(flag) break; } printf("Case %d: ", ++ant); if(flag) printf("Yes\n"); else printf("No\n"); gets(ch); } }
https://vjudge.net/contest/280903#problem/P要记录最短路径,用pre数组把每个元素前面的元素记录下来,在松弛的时候。
HDU1595,题意:可以任意破坏一条路,然后求此时最大的最短路,枚举,把开始的最短路一条一条消除,然后比较得出答案
#include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<utility> using namespace std; typedef pair<int,int>pii; const int inf = 1e9 + 7; const int maxm = 1005; int n, m; int d[maxm]; int mapp[maxm][maxm]; int pre[maxm]; void Dijkstra(int a, int flag){ for(int i = 1; i <= n; i++) d[i] = inf; d[a] = 0; priority_queue<pii,vector<pii>,greater<pii> >q; q.push(make_pair(0, a)); while(!q.empty()){ pii x = q.top(); q.pop(); int u = x.second; if(d[u] != x.first) continue; for(int v = 1; v <= n; v++){ int tmp = d[u] + mapp[u][v]; if(mapp[u][v] != inf && d[v] > tmp){ if(flag) pre[v] = u;//在松弛的时候记录每个元素之前的元素 d[v] = tmp; q.push(make_pair(d[v],v)); } } } } char ch[3]; int main(){ int x, y, z; while(~scanf("%d%d",&n,&m)){ for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { mapp[i][j] = inf; } } memset(pre, -1, sizeof(pre)); for(int i = 1; i <= m; i++){ scanf("%d%d%d",&x,&y,&z); mapp[x][y] = mapp[y][x] = z; } Dijkstra(1, 1); int maxx = -1, dis; for(int i = n; i != 1; i = pre[i]){ dis = mapp[i][ pre[i] ];//保存值。 mapp[i][ pre[i] ] = mapp[ pre[i] ][i] = inf; Dijkstra(1, 0); maxx = max(maxx, d[n]); mapp[i][ pre[i] ] = mapp[ pre[i] ][i] = dis; } printf("%d\n", maxx); gets(ch); } return 0; }
记录最短路径然后输出
void putpath() {
stack<int> path;
int now = t;
while(1) {
path.push(now);
if(now == s) {//S是原点
break;
}
now = pre[now];
}
while(!path.empty()) {
now = path.top();
path.pop();
printf("%d\n", now);
}
这个题目有向图1到每个点的距离加上每个点到1的距离之和,直接把有向边倒过来存。HDU1535
Q - Harry Potter and the Final Battle
HDU - 3986 和上面一题差不多,只是有重边,上面是用数组做得,下面这个使用vector做得,更好
#include<cstring> #include<cstdio> #include<iostream> #include<queue> using namespace std; typedef pair<int,int>pii; const int inf = 1e8; const int maxm = 1005; int n, m; struct edge{ int to, dis, id; edge(int to = 0, int dis = 0, int id = 0) : to(to), dis(dis), id(id) {}; bool operator < (const edge &a) const { return dis < a.dis; } }; priority_queue<pii, vector<pii>, greater<pii> >q; vector<edge> ve[maxm]; int des[maxm * maxm], ro[maxm], d[maxm], pre[maxm];
//des数组记录这条边是否已经被损坏,ro记录最短路上的边的id,pre记录最短路依次经过的点 void Dijkstra(int a, int flag){ for(int i = 1; i <= n; i++) d[i] = inf; d[a] = 0; while(!q.empty()) q.pop(); q.push(make_pair(0, a)); while(!q.empty()){ pii x = q.top(); q.pop(); int u = x.second; if(d[u] < x.first) continue; for(int v = 0; v < ve[u].size(); v++) { edge e = ve[u][v]; if(des[e.id]) continue;//如果这条路已经被损坏,则不计算 if(d[e.to] > d[u] + e.dis) { if(flag){//只记录没损坏前的最短路的边以及点 pre[e.to] = u; ro[e.to] = e.id; } d[e.to] = d[u] + e.dis; q.push(make_pair(d[e.to], e.to)); } } } } int t; int main(){ int x, y, z; scanf("%d", &t); while(t--){ scanf("%d%d",&n,&m); memset(pre, 0, sizeof(pre)); memset(des, 0, sizeof(des)); memset(ro, 0, sizeof(ro)); for(int i = 1; i <= n; i++) { ve[i].clear(); } for(int i = 1; i <= m; i++){ scanf("%d%d%d",&x,&y,&z); ve[x].push_back(edge(y, z, i)); ve[y].push_back(edge(x, z, i)); } Dijkstra(1, 1); int maxx = -1, fl = 0; if(d[n] >= inf) { printf("-1\n"); continue; } for(int i = n; i != 1; i = pre[i]) { // dis = mapp[i][ pre[i] ]; // mapp[i][ pre[i] ] = mapp[ pre[i] ][i] = inf; des[ ro[i] ] = 1;//损坏最短路上的一条边然后在后面复原。 Dijkstra(1, 0); des[ ro[i] ] = 0; maxx = max(maxx, d[n]); // printf("%d\n", maxx); if(maxx >= inf) { fl = 1; break; } // mapp[i][ pre[i] ] = mapp[ pre[i] ][i] = dis; } if(fl) printf("-1\n"); else printf("%d\n", maxx); } return 0; }
find the mincost route
杭州有N个景区,景区之间有一些双向的路来连接,现在8600想找一条旅游路线,这个路线从A点出发并且最后回到A点,假设经过的路线为V1,V2,....VK,V1,那么必须满足K>2,就是说至除了出发点以外至少要经过2个其他不同的景区,而且不能重复经过同一个景区。现在8600需要你帮他找一条这样的路线,并且花费越少越好。
最小环问题
https://blog.csdn.net/olga_jing/article/details/49928443
#include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int maxm = 105; const int inf = 1e6; int mapp[maxm][maxm], d[maxm][maxm]; int n, m, minn; int l, r, w;
算法思想;
*Floyd算法是按照顶点的编号增加的顺序更新最短路径的;
*如果存在最小环,则会在这个环中的点编号最大的那个点u更新最短路径之前发现这个环;
*即当点u被拿来更新i到j的最短路径的时候,可以发现这个闭合环路;
*发现的方法是,更新最短路径前,遍历i,j点对,一定会发现某对i到j的最短路径长度:
*dist[i][j]+map[j][u]+map[u][i]!=INF,这时s的i和j是当前环中挨着点u的两个点;
*因为在之前的最短路径更新过程中,u没有参与更新,所以dist[i][j]所表示的路径中不会有点u,即一定为一个环;
*
*如果在每个新的点拿来更新最短路径之前遍历i和j验证上面的式子,虽然不能遍历到所有的环;
*但是由于dist[i][j]是i到j点的最短路径m所以肯定可以遍历到最小的环;
*
*如果有负权环,则该算法失效,因为包含负环的图上,dist[i][j]已经不能保证i到j的路径上不会经过同一个点多次了;
void floy() { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { d[i][j] = mapp[i][j]; } } for(int k = 1; k <= n; k++) { for(int i = 1; i < k; i++) { for(int j = 1; j < i; j++) { minn = min(minn, d[i][j] + mapp[j][k] + mapp[k][i]); } } for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { if(d[i][k] + d[k][j] < d[i][j]) { d[i][j] = d[i][k] + d[k][j]; } } } } } int main() { while(~scanf("%d%d", &n, &m)) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++){ if(i == j) mapp[i][j] = 0; else mapp[i][j] = inf; } } minn = inf; while(m--){ scanf("%d%d%d", &l, &r, &w); if(w < mapp[l][r]) mapp[l][r] = mapp[r][l] = w; } floy(); if(minn >= inf) printf("It's impossible.\n"); else printf("%d\n", minn); } return 0; }
昂贵的聘礼
中文题
https://www.cnblogs.com/farway17/p/10747216.html 一个讲二进制分组的题目
https://www.cnblogs.com/kkrisen/p/3243273.html
https://blog.csdn.net/qq_30796379/article/details/80343721
超级源点法,0这一点是原点。
因为这种题目不止边上有权值, 点上也有权值,所以取一个原点,把其他点的权值表示成0点到其他点的边上的权值。
#include<cstdio> #include<algorithm> #include<cstring> #include<queue> using namespace std; const int maxm = 105; const int inf = 0x3f3f3f3f; struct edge{ int to, dis; edge(int to = 0, int dis = 0) : to(to), dis(dis) {}; }; int d[maxm], rak[maxm]; vector<edge> ve[maxm]; typedef pair<int, int> pii; int n, m, w, u, v, x, y; priority_queue<pii, vector<pii>, greater<pii> > pq; void dijstela() { while(!pq.empty()) pq.pop(); for(int i = 1; i <= m; i++) { d[i] = inf; } d[0] = 0; pq.push(make_pair(d[0], 0)); while(!pq.empty()) { pii p = pq.top(); pq.pop(); int dis = p.second; if(d[dis] < p.first) continue; for(int i = 0; i < ve[dis].size(); i++) { edge e = ve[dis][i]; if(rak[e.to] < rak[0] || rak[e.to] > rak[0] + n) continue; if(d[e.to] > d[dis] + e.dis) { d[e.to] = d[dis] + e.dis; pq.push(make_pair(d[e.to], e.to)); } } } } int main() { scanf("%d%d", &n, &m); for(int i = 0; i <= m; i++) { ve[i].clear(); } for(int i = 1; i <= m; i++) { scanf("%d%d%d", &w, &u, &v); ve[0].push_back(edge(i, w)); rak[i] = u; while(v--) { scanf("%d%d", &x, &y); ve[x].push_back(edge(i, y)); } } int res = inf; for(int i = 1; i <= m; i++) { rak[0] = rak[i]; dijstela(); res = min(res, d[1]); } printf("%d\n", res); return 0; }
spfa记录最短路径,都差不多,在松弛的时候记录前一个点。
#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <vector> #include <queue> #include <algorithm> using namespace std; const int INF=1e15; typedef struct{ int to; int val; }Point; int n,m,c; vector<Point> map[120]; int dis[120]; int path[120]; void SPFA() { for(int i=2;i<=n;i++) dis[i]=INF; dis[1]=0; queue<int>q; q.push(1); while(!q.empty()) { int u=q.front(); q.pop(); for(int i=0;i<map[u].size();i++) { Point v=map[u][i]; if(dis[v.to]>dis[u]+v.val) { dis[v.to]=dis[u]+v.val; path[v.to]=u; //存每个点的前一个点 q.push(v.to); } } } } int main() { //n为顶点数,m为边数,c为终点 while(scanf("%d%d%d",&n,&m,&c)!=EOF) { memset(path,0,sizeof(path)); for(int i=0;i<=n;i++) map[i].clear(); for(int i=1;i<=m;i++) { //u到v有一条有向边,权值为e int u,v,e; scanf("%d%d%d",&u,&v,&e); Point s; s.to=v; s.val=e; map[u].push_back(s); } SPFA(); int num[120]; int cnt=0; printf("%d\n",dis[c]); //最短路径长 printf("1->"); //起始都是从1开始出发 for(int i=c;i!=1;i=path[i]) { num[cnt++]=i; } for(int i=cnt-1;i>0;i--) { printf("%d->",num[i]); } printf("%d\n",num[0]); } return 0; }
迪杰斯特拉求最短路条数以及并输出最短路径中点和最大的那条的路径。spfa的也是一样的。
堆优化的差不多
#include <cstdio> #include <algorithm> #include <iostream> #include <cstring> #include <stack> using namespace std; const int maxn=1e3; const int INF=1e8; int n,m,st,en,x,y,z; int val[maxn],valsum[maxn],path[maxn],pathsum[maxn];//val储存每个点的值,valsum储存到点【i】前的点值和,path储存点【i】前那个点的号,pathsum储存到点【i】的最短路的条数 int d[maxn],vis[maxn],G[maxn][maxn]; void dijkstra() { for(int i=0;i<n;i++) d[i]=G[st][i]; d[st]=0; pathsum[st]=1;//初始化起点的最短路的条数是1 int min1,p; for(int i=1; i<=n; i++) { min1=INF; for(int j=0; j<n; j++) { if(!vis[j] && d[j]<min1) { min1=d[j]; p=j; } } vis[p]=1; for(int j=0; j<n; j++) { if(!vis[j] && d[j]>d[p]+G[p][j]) { d[j]=d[p]+G[p][j]; pathsum[j]=pathsum[p];//当松弛时,到【j】和到【p】的最短路的条数相同 valsum[j]=valsum[p]+val[j];//松弛时直接加上更新后的点值 path[j]=p;//记录上一个点 } else if(!vis[j] && d[j]==d[p]+G[p][j]) { pathsum[j]+=pathsum[p];//当相等时,到【j】的加上到【p】的 if(valsum[j]<valsum[p]+val[j]) { valsum[j]=valsum[p]+val[j];//当相等时加上大的那个 path[j]=p;//相等时记录大的那个点 } } } } } void P()//输出路径 { int tmp; stack<int>si; while(!si.empty()) si.pop(); si.push(en);//从最后的那个点开始逆序存到堆栈里 while (st!=en) { tmp=path[en]; si.push(tmp); en=tmp; } cout << si.top(); si.pop(); while(!si.empty()) { cout << ' ' << si.top(); si.pop(); } cout << endl; } void inition() { memset(path,0,sizeof(path)); memset(vis,0,sizeof(vis)); memset(pathsum,0,sizeof(pathsum)); for(int i=0; i<n; i++) { for(int j=0; j<n; j++) { if(i==j) G[i][j]=0; else G[i][j]=INF; } valsum[i]=val[i]; } } int main() { scanf("%d%d%d%d",&n,&m,&st,&en); for(int i=0; i<n; i++) scanf("%d",&val[i]); inition(); for(int i=1; i<=m; i++) {scanf("%d%d%d",&x,&y,&z);G[x][y]=z;G[y][x]=z;}//无向图 dijkstra(); printf("%d %d\n",pathsum[en],valsum[en]); P(); return 0; }
floyd记录路径的方法
void out(int i,int j) {
//可以加一个i==j则不用算。 if(path[i][j]==-1) return ; out(i,path[i][j]); cout<<path[i][j]; out(path[i][j],j); //先开始把数组元素初始化为-1。 }
for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { if(dis[i][j]>dis[i][k]+dis[k][j]) { dis[i][j]=dis[i][k]+dis[k][j]; path[i][j]=k;//这就是记录路径的数组了。 } }
HDU1385
floyd的另一种方法
#include<cstdio> #include<cstring> #define INF 1e9 using namespace std; const int maxn = 100+20; int n; int cost[maxn]; int dist[maxn][maxn];//最短距离 int path[maxn][maxn];//path[i][j]保存了从i到j路径的第一个点(除i以外) void floyd() { for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) path[i][j]=j; for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(dist[i][k]<INF && dist[k][j]<INF) { if(dist[i][j] > dist[i][k]+dist[k][j]+cost[k]) { dist[i][j] = dist[i][k]+dist[k][j]+cost[k]; path[i][j] = path[i][k]; } else if(dist[i][j] == dist[i][k]+dist[k][j]+cost[k] && path[i][j]>path[i][k]) { path[i][j]=path[i][k]; } } } int main() { while(scanf("%d",&n)&&n){ for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){ scanf("%d",&dist[i][j]); if(dist[i][j]==-1)dist[i][j]=INF; } for(int i=1;i<=n;i++)scanf("%d",&cost[i]); floyd(); int u,v; while(scanf("%d%d",&u,&v)){ if(u==-1&&v==-1)break; int from=u; printf("From %d to %d :\n",u,v); printf("Path: "); while(true){ if(u!=v){ printf("%d-->",u); u=path[u][v]; } else{ printf("%d\n",u); break; } } printf("Total cost : %d\n\n",dist[from][v]); } } return 0; }
https://blog.csdn.net/u011483306/article/details/45533237





