后缀自动机
https://oi-wiki.org/string/sam/#_5
oiwiki网上的
https://blog.csdn.net/thy_asdf/article/details/51569443
这个博客讲了很多题。
广义后缀自动机的意思是在后缀自动机上添加上多个串,每次添加一个串的时候把last设为0.
!!后缀链接link(v)指向在不同等价类中的w的最长后缀。
后缀自动机的right数组,首先只有那些是前缀的节点的right的值等于1,然后通过之后的fail转移来是其他点的right值++。
比如说abcc,首先a,ab,abc,abcc的right值都等于1,然后通过fail指针转移,那么bcc这个点的right值将++。
直观上,字符串的 SAM 可以理解为给定字符串的 所有子串 的压缩形式。值得注意的事实是,SAM 将所有的这些信息以高度压缩的形式储存。对于一个长度为 n 的字符串,它的空间复杂度仅为 O(n) 。此外,构造 SAM 的时间复杂度仅为O(n) 。准确地说,一个 SAM 最多有 2n-1 个节点和 3n-4 条转移边。
第一张nex数组,第二张fail树。
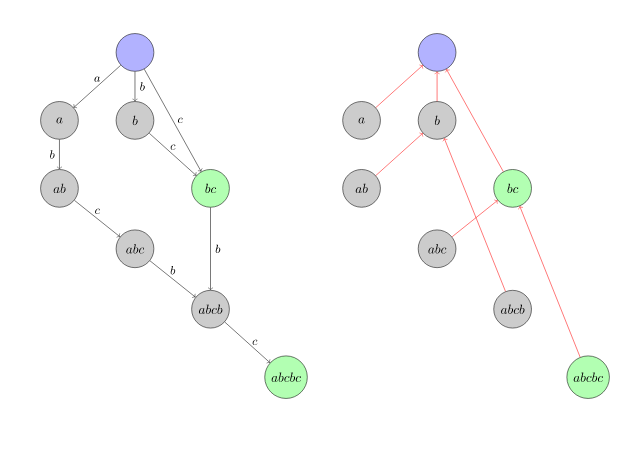
//nex数组是当前能匹配到的最长子串,fail是到当前节点所能到的最长后缀的点(必须是存在的)
//#include<bits/stdc++.h> #include<cstdio> #include<cstring> #include<queue> #include<vector> #include<algorithm> using namespace std; const int maxn = 2e4 + 5; const int maxc = 180;//如果太大可以用map const int mod = 1e9 + 7; const int inf = 0x3f3f3f3f; typedef long long ll; int len[maxn * 2]; //最长子串的长度(该节点字串数量=len[x]-len[fail[x]]) int fail[maxn * 2]; //后缀链接,fail节点的right集合比他自身的大,fail节点代表的串是他自身代表串的子串(后缀子串) int cnt[maxn * 2]; //被后缀连接的数量,方法一求拓扑排序时需要。 int nex[maxn * 2][maxc]; //状态转移(尾部加一个字符的下一个状态)(图),如果不只是字母,而是很大的话可以用map. int sz; //节点编号 int last; //最后节点 ll epos[maxn * 2]; // enpos数(该状态子串出现数量) ll sum[maxn * 2], rak[maxn * 2]; //求拓扑序是用的数组。 int val[maxn], mi[maxn * 2], ma[maxn * 2]; /** 初始化 **/ void init() { //初始化 last = sz = 1; //1表示root起始点 空集 fail[1] = len[1] = 0; } /** SAM建图 **/ void Extend(int c) { //插入字符,为字符ascll码值 int cur = ++sz; //创建一个新节点cur; len[cur] = len[last] + 1; // 长度等于最后一个节点+1 mi[cur] = ma[cur] = len[cur]; epos[cur] = 1; //接受节点子串除后缀连接还需加一 int p; //第一个有C转移的节点; for (p = last; p && !nex[p][c]; p = fail[p]) nex[p][c] = cur;//沿着后缀连接 将所有没有字符c转移的节点直接指向新节点 if (!p) { fail[cur] = 1; cnt[1]++; //全部都没有c的转移 直接将新节点后缀连接到起点 } else { int q = nex[p][c]; //p通过c转移到的节点 if (len[p] + 1 == len[q]) //pq是连续的 fail[cur] = q; cnt[q]++; //将新节点后缀连接指向q即可,q节点的被后缀连接数+1 else { int nq = ++sz; //不连续 需要复制一份q节点 len[nq] = len[p] + 1; //令nq与p连续 fail[nq] = fail[q]; //因后面fail[q]改变此处不加cnt memcpy(nex[nq], nex[q], sizeof(nex[q])); //复制q的信息给nq for (; p&&nex[p][c] == q; p = fail[p]) nex[p][c] = nq; //沿着后缀连接 将所有通过c转移为q的改为nq fail[q] = fail[cur] = nq; //将cur和q后缀连接改为nq cnt[nq] += 2; // nq增加两个后缀连接 } } last = cur; //更新最后处理的节点 } char s1[maxn], s2[maxn]; /** 求一个串每个长度的所有子串中,出现最多的次数spoj8222 **/ /** 方法一:bfs的拓扑排序,不是主要方法 **/ //求npos数,即该节点子串出现次数 void GetNpos(char ch[], int len1) { for(int i = 0; i < len1; i++) Extend(ch[i] - 'a'); queue<int>q; for (int i = 1; i <= sz; i++) if (!cnt[i]) q.push(i); //将所有没被后缀连接指向的节点入队 while (!q.empty()) { int x = q.front(); q.pop(); epos[fail[x]] += epos[x]; //子串数量等于所有后缀连接指向该节点的子串数量和+是否为接受节点 if (--cnt[fail[x]] == 0)q.push(fail[x]); //当所有后缀连接指向该节点的处理完毕后再入队 } } //求出所有长度为k的子串中出现次数最多的子串出现次数 void GetSubMax() { ll a[maxn]; scanf("%s", s1);//方法一长度为i的子串出现最大次数 int len1 = strlen(s1); GetNpos(s1, len1); for (int i = 1; i <= sz; i++) a[len[i]] = max(a[len[i]], epos[i]); //长度≤k的子串中出现次数最多的子串出现次数的最小值 for (int i = len1 - 1; i >= 1; i--) a[i] = max(a[i], a[i + 1]); //求一遍后缀最大值就是答案 for (int i = 1; i <= len1; i++) printf("%lld\n", a[i]); } /** 方法二数组的逆拓扑序 **/ void getmaxlen() { ll num[maxn * 2];//方法二长度为i的子串出现最大次数。 init(); scanf("%s", s1); int len1 = strlen(s1); for(int i = 0; i < len1; i++) Extend(s1[i] - 'a'); //下面是计数排序的思想。相当于找一个数前面有多少个数,从而知道这个数排在哪。 for(int i = 1; i <= sz; i++) sum[len[i] ]++; for(int i = 1; i <= len1; i++) sum[i] += sum[i - 1]; for(int i = 1; i <= sz; i++) rak[sum[len[i] ]-- ] = i; for(int i = sz; i >= 1; i--) { int x = rak[i]; epos[fail[x] ] += epos[x]; } for(int i = 1; i <= sz; i++) num[len[i] ] = max(num[len[i] ], epos[i]); for(int i = len1 - 1; i >= 1; i--) num[i] = max(num[i], num[i + 1]); for(int i = 1; i <= len1; i++) printf("%lld\n", num[i]); } /** 求不相同字串数量 **/ void GetSubNum() { ll ans = 0; for (int i = 2; i <= sz; i++) ans += len[i] - len[fail[i]]; //一状态子串数量等于len[i]-len[fail[i]] printf("%lld\n",ans); } /** 求多个字符串的最长公共子串spoj1812 **/ void getnlcs() { ll maxnlcs[maxn * 2]; //求多个子串最长公共子串时,每个串来匹配时能匹的最长长度。 ll ans[maxn * 2]; //求多个子串的最长公共子串时的结果数组。 init(); scanf("%s", s1); int len1 = strlen(s1); for(int i = 0; i < len1; i++) Extend(s1[i] - 'a'); for(int i = 1; i <= sz; i++) ans[i] = len[i]; //下面是计数排序的思想。相当于找一个数前面有多少个数,从而知道这个数排在哪。 for(int i = 1; i <= sz; i++) sum[len[i] ]++; for(int i = 1; i <= len1; i++) sum[i] += sum[i - 1]; for(int i = 1; i <= sz; i++) rak[sum[len[i] ]-- ] = i; while(~scanf("%s", s2)) { memset(maxnlcs, 0, sizeof(maxnlcs)); int len2 = strlen(s2); int p = 1; ll tmp = 0; for(int i = 0; i < len2; i++) { int x = s2[i] - 'a'; if(nex[p][x]) { tmp++; p = nex[p][x]; } else { while(p && !nex[p][x]) p = fail[p]; if(!p) { tmp = 0; p = 1; } else { tmp = len[p] + 1; p = nex[p][x]; } } maxnlcs[p] = max(maxnlcs[p], tmp); } //首先如果一个点能够匹配到的话,那么他的fail指针的点也一定可以匹配到,因为fail指针的 //的点是原来节点的子串,所以下面的节点要先更新,然后更新其fail指针的。这个需要逆拓扑。 for(int i = sz; i >= 1; i--) { ll x = rak[i]; ans[x] = min(ans[x], maxnlcs[x]); if(maxnlcs[x] && fail[x]) maxnlcs[fail[x] ] = len[fail[x] ]; } // printf("scsc\n"); } ll res = 0; for(int i = 1; i <= sz; i++) res = max(ans[i], res); printf("%lld\n", res); } /** 求两个字符串的最长公共子串。spoj1811 直接根据后缀自动机的状态转移图来遍历,如果存在这个字符就继续往下走,不存在则开始跳fail, 直到找到存在那个字符的,此时只有这个fail点与最开始的点后缀相同。 **/ void getlcs() { init(); scanf("%s%s", s1, s2); int len1 = strlen(s1), len2 = strlen(s2); for(int i = 0; i < len1; i++) { Extend(s1[i] - 'a'); } int ans = 0, tmp = 0, p = 1; for(int i = 0; i < len2; i++) { int x = s2[i] - 'a'; if(nex[p][x]) { tmp++; p = nex[p][x]; } else { while(p && !nex[p][x]) p = fail[p]; if(!p) { tmp = 0; p = 1; } else { tmp = len[p] + 1; p = nex[p][x]; } } ans = max(ans, tmp); } printf("%d\n", ans); } /** bzoj3998 求一个字符串中第K大的串,op=0代表相同的串在不同位置只算一次,op=1代表可以算多次。 所以先求出所有子串的可能出现次数。epos数组 然后求出某个点以这个点开头的字符串数量。num数组。 然后在dfs去找。 **/ ll num[maxn * 2]; void dfsk(int rt, int rk) { if(rk <= epos[rt]) return; rk -= epos[rt]; for(int i = 0; i < 26; i++) { int v = nex[rt][i]; if(v) { if(rk <= num[v]) { putchar('a' + i); dfsk(v, rk); return; } else rk -= num[v]; } } } void getk() { scanf("%s", s1); int op, k; scanf("%d%d", &op, &k); init(); int len1 = strlen(s1); for(int i = 0; i < len1; i++) Extend(s1[i] - 'a'); //下面是计数排序的思想。相当于找一个数前面有多少个数,从而知道这个数排在哪。 for(int i = 1; i <= sz; i++) sum[len[i] ]++; for(int i = 1; i <= len1; i++) sum[i] += sum[i - 1]; for(int i = 1; i <= sz; i++) rak[sum[len[i] ]-- ] = i; for(int i = sz; i >= 1; i--) { int x = rak[i]; if(op == 1) epos[fail[x] ] += epos[x]; else epos[x] = 1; } epos[1] = 0; for(int i = sz; i >= 1; i--) { int x = rak[i]; num[x] = epos[x]; for(int j = 0; j < 26; j++) { int v = nex[x][j]; if(v) num[x] += num[v]; } } // for(int i = 1; i <= sz; i++) printf("%lld\n", epos[i]); if(num[1] < k) puts("-1"); else { dfsk(1, k); puts(""); } } /** 求变化趋势相同的子串且长度大于等于5.poj1743 因为是变化趋势,所以要先差分一下,那么就相当于差分数组建后缀自动机,然后找长度大于等于4的子串, 且没有重合的点。注意多组数据时的初始化。
后缀自动机上的每个状态都有一个right集合代表到达该状态的子串在原串中出现位置的右端点。
所以我们只需要知道每个状态最靠左和最靠右的端点分别在哪里,
如果两点直接的差不小于该点的len[i]就说明这个该位置代表的子串重复出现且没有重合,然后用len[i]更新答案即可 **/ int tmp[maxn * 2]; int cmp(int x, int y) { return len[x] > len[y]; } void getSameTend() { int n; while(~scanf("%d", &n)) { if(n == 0) break; init(); memset(mi, inf, sizeof(mi)); memset(ma, 0, sizeof(ma)); memset(nex, 0, sizeof(nex)); memset(fail, 0, sizeof(fail)); memset(sum, 0, sizeof(sum)); for(int i = 1; i <= n; i++) scanf("%d", &val[i]); for(int i = 1; i < n; i++) val[i] = val[i + 1] - val[i], Extend(val[i] + 88); for(int i = 1; i <= sz; i++) sum[len[i] ]++; for(int i = 1; i < n; i++) sum[i] += sum[i - 1]; for(int i = 1; i <= sz; i++) rak[sum[len[i] ]-- ] = i; for(int i = sz; i > 0; i--) { int x = rak[i]; ma[fail[x] ] = max(ma[fail[x] ], ma[x]); mi[fail[x] ] = min(mi[fail[x] ], mi[x]); } int ans = 0; for(int i = sz; i >= 1; i--) { ans = max(ans, min(ma[i] - mi[i], len[i])); } ans++; if(ans < 5) ans = 0; printf("%d\n", ans); } } int main() { getlcs(); getnlcs(); getmaxlen(); getk(); getSameTend(); return 0; }
//#include<bits/stdc++.h> #include<cstdio> #include<cstring> #include<queue> #include<vector> #include<algorithm> using namespace std; const int maxn = 2e5 + 5; const int maxc = 30;//如果太大可以用map const int mod = 1e9 + 7; const int inf = 0x3f3f3f3f; typedef long long ll; int len[maxn * 2]; //最长子串的长度(该节点字串数量=len[x]-len[fail[x]]) int fail[maxn * 2]; //后缀链接(最短串前部减少一个字符所到达的状态) int cnt[maxn * 2]; //被后缀连接的数量,方法一求拓扑排序时需要。 int nex[maxn * 2][maxc]; //状态转移(尾部加一个字符的下一个状态)(图),如果不只是字母,而是很大的话可以用map. int sz; //节点编号 int last; //最后节点 ll epos[maxn * 2]; // enpos数(该状态子串出现数量) ll sum[maxn * 2], rak[maxn * 2]; //求拓扑序是用的数组。 ll fasum[maxn * 2];//表示当前节点与其fail节点以及fail节点的fail节点的所有子串之和。 /** 初始化 **/ void init() { //初始化 last = sz = 1; //1表示root起始点 空集 fail[1] = len[1] = 0; } /** SAM建图 **/ void Extend(int c) { //插入字符,为字符ascll码值 int cur = ++sz; //创建一个新节点cur; len[cur] = len[last] + 1; // 长度等于最后一个节点+1 // mi[cur] = ma[cur] = len[cur]; epos[cur] = 1; //接受节点子串除后缀连接还需加一 int p; //第一个有C转移的节点; for (p = last; p && !nex[p][c]; p = fail[p]) nex[p][c] = cur;//沿着后缀连接 将所有没有字符c转移的节点直接指向新节点 if (!p) { fail[cur] = 1; cnt[1]++; //全部都没有c的转移 直接将新节点后缀连接到起点 } else { int q = nex[p][c]; //p通过c转移到的节点 if (len[p] + 1 == len[q]) { //pq是连续的 fail[cur] = q; cnt[q]++; //将新节点后缀连接指向q即可,q节点的被后缀连接数+1 } else { int nq = ++sz; //不连续 需要复制一份q节点 len[nq] = len[p] + 1; //令nq与p连续 fail[nq] = fail[q]; //因后面fail[q]改变此处不加cnt memcpy(nex[nq], nex[q], sizeof(nex[q])); //复制q的信息给nq for (; p&&nex[p][c] == q; p = fail[p]) nex[p][c] = nq; //沿着后缀连接 将所有通过c转移为q的改为nq fail[q] = fail[cur] = nq; //将cur和q后缀连接改为nq cnt[nq] += 2; // nq增加两个后缀连接 } } last = cur; //更新最后处理的节点 } char s1[maxn], s2[maxn]; /** HYSBZ - 4566 找A串的所有子串在B串中的出现次数。 对于B匹配到的每个点,得到的次数是当前节点在A中该串出现的次数*该节点管辖的子串,然后 加上他所有fail节点的出现次数*字符串个数。 因为如果当前节点能匹配到了,那么他的fail节点也能匹配到。 **/ void getallsame() { init(); scanf("%s%s", s1, s2); int len1 = strlen(s1); int len2 = strlen(s2); for(int i = 0; i < len1; i++) Extend(s1[i] - 'a'); for(int i = 1; i <= sz; i++) sum[len[i] ]++; for(int i = 1; i <= len1; i++) sum[i] += sum[i - 1]; for(int i = 1; i <= sz; i++) rak[sum[len[i] ]-- ] = i; for(int i = sz; i >= 1; i--) { int x = rak[i]; epos[fail[x] ] += epos[x]; }
//这个是正着来的。 for(int i = 1; i <= sz; i++) { int x = rak[i]; fasum[x] = fasum[fail[x] ] + epos[x] * (len[x] - len[fail[x] ]); } ll ans = 0; int p = 1, val = 0; for(int i = 0; i < len2; i++) { int x = s2[i] - 'a'; if(nex[p][x]) { p = nex[p][x]; val++; } else { while(p && !nex[p][x]) p = fail[p]; if(!p) { p = 1; val = 0; } else { val = len[p] + 1; p = nex[p][x]; } } ans += fasum[fail[p] ] + (val - len[fail[p] ]) * epos[p]; } printf("%lld\n", ans); } int main() { getallsame(); return 0; }
bzoj2882:用后缀自动机实现最小表示法。把串复制一遍,构建后缀自动机,每次选择最小的边转移即可
因为字符集很大,所以转移边用map来存即可
#include<map> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define it map<int,int>::iterator const int maxn=1200010; using namespace std; int n,s[maxn]; void read(int &x){ char ch; for (ch=getchar();!isdigit(ch);ch=getchar()); for (x=0;isdigit(ch);ch=getchar()) x=x*10+ch-'0'; } struct Tsam{ map<int,int> ch[maxn]; int dis[maxn],fa[maxn],root,last,tot; int newnode(int v){dis[++tot]=v;return tot;} void init(){last=root=++tot;} void add(int x){ int p=last,np=newnode(dis[p]+1); last=np; for (;p&&!ch[p].count(x);p=fa[p]) ch[p][x]=np;//printf("char=%d %d\n",x,p); if (!p) fa[np]=root; else{ int q=ch[p][x]; if (dis[q]==dis[p]+1) fa[np]=q; else{ int nq=newnode(dis[p]+1); ch[nq]=ch[q]; fa[nq]=fa[q]; fa[np]=fa[q]=nq; for (;ch[p][x]==q;p=fa[p]) ch[p][x]=nq;//printf("qp: char=%d %d %d\n",x,p,fa[p]); } } } void build(){ init(); for (int i=1;i<=n;i++) add(s[i]); for (int i=1;i<=n;i++) add(s[i]); } void getmin(){ for (int i=1;i<=tot;i++){ it iter=ch[i].begin(); //printf("id=%d char=%d minson=%d\n",i,iter->first,iter->second); } for (int i=1,p=root;i<=n;i++){ it iter=ch[p].begin(); printf(i==n?"%d\n":"%d ",iter->first); p=iter->second; //printf("p=%d %d\n",p,ch[p].begin()->second); } } }T; int main(){ //freopen("test.out","w",stdout); scanf("%d",&n); for (int i=1;i<=n;i++) read(s[i]); T.build(),T.getmin(); return 0; }
一道广义后缀自动机的题。
Description
Input
Output
输出一行n个整数,第i个整数表示第i个字符串的答案。
Sample Input
abc
a
ab
Sample Output
HINT
Source
广义后缀自动机?就是把一坨字符串建到一个后缀自动机上??
不过好难理解啊qwq。。
对于这题,首先我们要知道几个定理
1.节点i表示的本质不同的字符串可以由len[i]−len[fa[i]]得到
2.一个串的子串 等价于 一个串所有前缀的所有后缀
这样子串就转换为求一个串的前缀的所有后缀的问题
前缀可以枚举,问题转换为求一个字符串的各个后缀在其他字符串中出现了多少次
这样我们可以把广义后缀自动机建出来,然后暴力沿着parent边跑,这样可以枚举出所有后缀
同时为了不重复枚举,我们需要记录下每个后缀是否已经被枚举过了
这样我们就可以知道一个状态出现的次数是否>=K,接下来我们只要统计出这个状态出现的次数就行了
根据定理1,这个很好统计
然后就做完啦
#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int MAXN = 1e6 + 10; string s[MAXN]; int N, K; int fa[MAXN], len[MAXN], ch[MAXN][26], root = 1, last = 1, tot = 1, times[MAXN]; void insert(int x) { int now = ++tot, pre = last; last = now; len[now] = len[pre] + 1; for(; pre && !ch[pre][x]; pre = fa[pre]) ch[pre][x] = now; if(!pre) fa[now] = root; else { int q = ch[pre][x]; if(len[q] == len[pre] + 1) fa[now] = q; else { int nows = ++tot; len[nows] = len[pre] + 1; memcpy(ch[nows], ch[q], sizeof(ch[q])); fa[nows] = fa[q]; fa[q] = fa[now] = nows; for(; pre && ch[pre][x] == q; pre = fa[pre]) ch[pre][x] = nows; } } } int vis[MAXN], sum[MAXN]; void GetTimes() {//求出每一个状态在几个字符串出现过 for(int i = 1; i <= N; i++) { int now = root; for(int j = 0; j < s[i].length(); j++) { now = ch[now][s[i][j] - 'a'];//枚举每一个前缀 int t = now; while(t && vis[t] != i) vis[t] = i, times[t]++, t = fa[t];//枚举每一个后缀 } } } void dfs(int x) { if(x == root || vis[x]) return ; vis[x] = 1; dfs(fa[x]); sum[x] += sum[fa[x]]; } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif ios::sync_with_stdio(0); cin >> N >> K; for(int i = 1; i <= N; i++) cin >> s[i]; for(int i = 1; i <= N; i++) { last = 1; for(int j = 0; j < s[i].length(); j++) insert(s[i][j] - 'a'); } GetTimes(); for(int i = 1; i <= tot; i++) sum[i] = (times[i] >= K) * (len[i] - len[fa[i]]);//i状态所表示的子串集合对答案的贡献 memset(vis, 0, sizeof(vis)); for(int i = 1; i <= tot; i++) dfs(i); for(int i = 1; i <= N; i++) { int ans = 0, now = root; for(int j = 0; j < s[i].length(); j++) now = ch[now][s[i][j] - 'a'], ans += sum[now]; //枚举前缀,算出每一个前缀所包含的后缀对答案啊的贡献 printf("%d ", ans); } return 0; }



