ac自动机
https://www.cnblogs.com/sclbgw7/p/9875671.html
讲的好的博客。
只有fail指针的模板,好像用不到,一般都是用last指针的模板。
void build() { queue<int>q; q.push(1); while(!q.empty()) { int x=q.front();q.pop(); for(int i=0;i<26;++i) { int c=ch[x][i]; if(!c){ch[x][i]=ch[fail[x]][i];continue;}//关键,把子节点改成fail节点的子节点 q.push(c); int fa=fail[x]; while(fa&&!ch[fa][i])fa=fail[fa]; fail[c]=ch[fa][i]; } } }
https://cn.vjudge.net/contest/301351#problem/A
习题
最基础的模板,即求一个文本串有多少个匹配的模式串。
#include<queue> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn = 5e5 + 5; const int N = 1e6 + 5; int tree[maxn][27]; int val[maxn]; int f[maxn]; int last[maxn]; int tot = 1; void inset(char s[]) { int root = 0; int len = strlen(s); for(int i = 0; i < len; i++) { int id = s[i] - 'a'; if(!tree[root][id]) { memset(tree[tot], 0, sizeof(tree[tot])); val[tot] = 0; tree[root][id] = tot++; } root = tree[root][id]; } val[root]++; } void getfail() { queue<int> q; f[0] = 0; for(int i = 0; i < 26; i++) { int u = tree[0][i]; if(u) { f[u] = 0; q.push(u); last[u] = 0; } } while(!q.empty()) { int now = q.front(); q.pop(); for(int i = 0; i < 26; i++) { int u = tree[now][i]; if(!u) { tree[now][i] = tree[f[now] ][i]; continue; } q.push(u); int v = f[now]; f[u] = tree[v][i]; last[u] = val[f[u] ] ? f[u] : last[f[u] ]; } } } int query(char s[]) { int now = 0, ans = 0; int len = strlen(s); for(int i = 0; i < len; i++) { now = tree[now][s[i] - 'a' ]; // for(int j = now; j && val[j] != -1; j = last[j]) { // ans += val[j]; // val[j] = -1; // } int tmp = now;
//如果匹配到根节点就停止,其他情况下如果val[tmp]等于0或1都加上,0加上不影响结果。 while(tmp) { ans += val[tmp]; val[tmp] = 0; tmp = last[tmp]; } } return ans; } char s[N]; int main() { int n, t; scanf("%d", &t); while(t--) { scanf("%d", &n); tot = 1; memset(tree[0], 0, sizeof(tree[0])); for(int i = 0; i < n; i++) { scanf("%s", s); inset(s); } getfail(); scanf("%s", s); printf("%d\n", query(s)); } return 0; }
DNA Sequence
https://www.cnblogs.com/LQLlulu/p/9344774.html
一到ac自动机加上矩阵快速幂的题目
题意
题目给出m(m<=10)个仅仅由A,T,C,G组成的单词(单词长度不超过10),然后给出一个整数n(n<=2000000000),问你用这四个字母组成一个长度为n的长文本,有多少种组成方法可以使得它不含任何一个给出的单词。
分析
当时一看以为是跟训练指南上(UVA11468)一样的题,感觉只有四个字母并且单词数量和长度也比较小,但是一看给出的n有点懵逼。如果再按照书上建立AC自动机以后直接跑DP的方法肯定是不行了。然后我们就要用到,递推利器,矩阵快速幂。
我们还是按照套路先把AC自动机建出来,然后将每个单词结点设为非法结点,题目变成在AC自动机中走n步不通过非法结点的方案数。然后设f[i][j]是当前在结点i,已经走了j步,且未走过非法结点的方案数。然后怎么转移呢?
f[i][j]=A(0,i)*f[0][j-1]+A(1,i)*f[1][j-1]+...+A(sz-1,i)f[sz-1][j-1]。其中A(i,j)的含义就是从i到j有几条直接连接的边。那么将这个dp方程拆开来看
f0[i]=A(0,0)*f[0][i-1]+A(1,0)*f[1][i-1]+....+A(sz-1,0)*fsz-1[i-1]
f1[i]=A(0,1)*f[0][i-1]+A(1,1)*f[1][i-1]+....+A(sz-1,1)*fsz-1[i-1]
.
.
fsz-1[i]=A(0,sz-1)*f[0][i-1]+A(1,sz-1)*f[1][i-1]+...+A(sz-1,sz-1)*fsz-1[i-1]
然后根据这个我们就很好建立转移矩阵
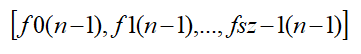 *
*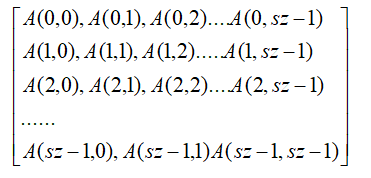
我的理解:每一项表示i到j的直接路径条数,如果两个矩阵相乘,就是i到j经过两条路径的种类数,最后只要得到0到其他点经过路径条数为n的数量,所以就只需要第一行的值相加就行。
然后为什么都要不是单词末尾。(不是很理解)现在的想法,因为最后的路径是由0开始一直走下来的,所以就不能经过单词末尾的节点,那些节点都是无效的。
(第一次学会用公式编辑器不过好像还是贼丑)
然后建立这个大的转移矩阵,矩阵的(i,j)为结点i到结点j的直接路径的条数,然后跑一个矩阵快速幂。
最后把从0到sz-1结点的f(n)的值全部加起来就是答案了。
对了这个题需要用long long
下面是代码
#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <queue> #include <map> using namespace std; const int maxnode=1100; const int MOD=100000; map<char,int>M; struct AC_Automata{ int ch[maxnode][4],f[maxnode],last[maxnode],val[maxnode],match[maxnode]; int sz; int idx(char c){ return M[c]; } void init(){ sz=1; memset(ch[0],0,sizeof(ch[0])); memset(match,0,sizeof(match)); val[0]=0; } void insert(char *s){ int n=strlen(s),u=0; for(int i=0;i<n;i++){ int c=idx(s[i]); if(!ch[u][c]){ ch[u][c]=sz; memset(ch[sz],0,sizeof(ch[sz])); val[sz++]=0; } u=ch[u][c]; } val[u]=1; match[u]=1; } void getFail(){ queue<int>q; last[0]=f[0]=0; for(int i=0;i<4;i++){ int u=ch[0][i]; if(u){ q.push(u); f[u]=last[u]=0; } } while(!q.empty()){ int r=q.front();q.pop(); for(int i=0;i<4;i++){ int u=ch[r][i]; if(!u){ ch[r][i]=ch[f[r]][i]; continue; } q.push(u); int v=f[r]; while(v&&!ch[v][i])v=f[v]; f[u]=ch[v][i]; match[u]|=match[f[u]]; } } } }ac; const int maxN=101; struct Matrix{ long long a[maxN][maxN]; void init(){ memset(a,0,sizeof(a)); for(int i=0;i<ac.sz;i++) a[i][i]=1; } }; Matrix mul(Matrix a,Matrix b){ Matrix res; for(int i=0;i<ac.sz;i++){ for(int j=0;j<ac.sz;j++){ res.a[i][j]=0; for(int k=0;k<ac.sz;k++){ res.a[i][j]+=a.a[i][k]*b.a[k][j]; res.a[i][j]%=MOD; } } } return res; } Matrix qpow(Matrix a,int k){ Matrix res; res.init(); while(k){ if(k%2)res=mul(res,a); a=mul(a,a); k/=2; } return res; } int n,m; char s[30]; int main(){ M['A']=0,M['C']=1,M['T']=2,M['G']=3; ac.init(); scanf("%d%d",&m,&n); for(int i=1;i<=m;i++){ scanf("%s",s); ac.insert(s); } ac.getFail(); Matrix A; for(int i=0;i<ac.sz;i++){ if(!ac.match[i]) for(int j=0;j<4;j++){ int u=ac.ch[i][j]; if(!ac.match[u]) A.a[i][u]++; } } /*for(int i=0;i<ac.sz;i++){ for(int j=0;j<ac.sz;j++){ printf("%d ",A.a[i][j]); } printf("\n"); }*/ Matrix S; S.a[0][0]=1; Matrix ANS; ANS=qpow(A,n); ANS=mul(S,ANS); long long ans=0; for(int i=0;i<=ac.sz;i++) ans+=ANS.a[0][i]; printf("%d\n",ans%MOD); return 0; }
蓝书上217面的题,ac自动机+概率dp,用的记忆化搜索。
给出一些字符和各自对应的选择概率,随机选择L次后将得到一个长度为L的随机字符串S(每次随机独立)。给出K个模式串,计算S不包含任何一个串的概率(即任何一个模板串都不是S的连续子串)
#include<cstdio> #include<cstring> #include<algorithm> #include<queue> using namespace std; const int SIGMA_SIZE = 64; const int MAXNODE = 500; int idx[256]; char s[30][30]; double prob[SIGMA_SIZE]; int n; struct AhoCorasickAutomata { int ch[MAXNODE][SIGMA_SIZE]; int f[MAXNODE]; int last[MAXNODE]; int match[MAXNODE]; int sz; void init() { sz = 1; memset(ch[0],0,sizeof(ch[0])); } //把模式串建立一颗字典树 void insert(char *s) { int u = 0,n = strlen(s); for(int i=0; i<n; i++) { int c = idx[s[i]]; if(!ch[u][c]) { memset(ch[sz],0,sizeof(ch[sz])); match[sz] = 0; ch[u][c] = sz++; } u = ch[u][c]; } match[u] = 1; } //根据bfs得到fail指针与last指针,在字典树上还增加失配边,及ch[u][i]的值变化了,有些本来是零的,根据fail数组的值,可能与之后匹配到的边连在了一起。 void getFail() { queue<int> q; f[0] = 0;
//与根节点相连的边,先初始化一下,并把有的字母push进来。 for(int c=0; c<SIGMA_SIZE; c++) { int u = ch[0][c]; if(u) { f[u] = 0; q.push(u); last[u] = 0; } } while(!q.empty()) { int r = q.front(); q.pop(); for(int c=0; c<SIGMA_SIZE; c++) { int u = ch[r][c];
//代替了最上面那个模板的while循环,每次下去一层就根据fail指针来增加失配边。 if(!u) { ch[r][c]=ch[f[r]][c]; continue; } q.push(u); int v = f[r]; // while(v&&!ch[v][c]) // v = f[v];
f[u] = ch[v][c]; last[u] = match[f[u] ] ? f[u] : last[f[u] ];
//这个是看这个节点是否是一个模式串的末尾,如果根据last匹配到的点是末尾,那么这个点也是某个模式串的末尾,因为last指针要么指向根节点,要么指向一个与当前匹配有相同后缀的点,如果是last节点的话,last匹配
//后没有字符,但是fail指针后面可能会有字符。 match[u] |=match[last[u]];
//这里相当于记录这个点是否是一个字符串的 } } } }; AhoCorasickAutomata ac; double d[MAXNODE][105]; int vis[MAXNODE][105]; double getProb(int u,int l) { if(!l) return 1.0; if(vis[u][l]) return d[u][l]; vis[u][l] = 1; double& ans = d[u][l]; ans = 0.0; for(int i=0; i<n; i++) { if(!ac.match[ac.ch[u][i]]) ans += prob[i]*getProb(ac.ch[u][i],l-1); } return ans; } int main() { int T; scanf("%d",&T); for(int kase = 1; kase<=T; kase ++) { int k,l; scanf("%d",&k); for(int i=0; i<k; i++) scanf("%s",s[i]); scanf("%d",&n); for(int i=0; i<n; i++) { char ch[9]; scanf("%s%lf",ch,&prob[i]); idx[ch[0]] = i; } ac.init(); for(int i=0; i<k; i++) ac.insert(s[i]); ac.getFail(); scanf("%d",&l); memset(vis,0,sizeof(vis)); printf("Case #%d: %.6lf\n",kase,getProb(0,l)); } return 0; }
DNA repair
ac自动机+dp;
跟矩阵那题思想差不多,只是这题要用dp来求最小值。
题意:有些DNA序列是致病的,给你以个长DNA序列,问最少需要修改多少次使得其不含致病序列。
首先是进行了一步转换,将其理解为在建好的Trie图上走len(序列长度)步,走的路不能包含致病序列。
然后就变成了一个dp,d[i][j]表示第i步走到j节点最少需要修改几次。那么要看所有能走到j节点的点,如果和s[i-1]相同,就不用修改,如果不同,修改次数加一,取较小的。
#include <bits/stdc++.h> using namespace std; #define CLR(m,a) memset(m,a,sizeof(m)) const int inf=0x3f3f3f3f; const int maxnode=50*20+10; const int sigma=4; struct AC{ int ch[maxnode][sigma],f[maxnode]; int match[maxnode]; int sz; int mp[128]; void init(){ CLR(match,0); mp['A']=0;mp['G']=1;mp['C']=2;mp['T']=3; CLR(ch[0],0); sz=1; } void inser(char *s){ int u=0,n=strlen(s); for(int i=0;i<n;i++){ int c=mp[s[i]]; if(!ch[u][c]){ CLR(ch[sz],0); ch[u][c]=sz++; } u=ch[u][c]; } match[u]=1; } void getfail(){ queue<int> q; f[0]=0; match[0]=0; for(int c=0;c<sigma;c++){ int u=ch[0][c]; if(u){ q.push(u); f[u]=0; } } while(!q.empty()){ int r=q.front(); q.pop(); for(int c=0;c<sigma;c++){ int u=ch[r][c]; if(!u){ ch[r][c]=ch[f[r]][c]; continue; } q.push(u); int v=f[r]; while(v&&!ch[v][c]) v=f[v]; f[u]=ch[v][c]; match[u]|=match[f[u]]; } } } }; AC ac; char s[maxnode]; int len; int dp[maxnode][maxnode]; void DP(){ CLR(dp,inf); dp[0][0]=0; for(int i=1;i<=len;i++){ for(int j=0;j<ac.sz;j++){ if(ac.match[j]) continue; for(int c=0;c<sigma;c++){ if(ac.match[ac.ch[j][c]]) continue; dp[i][ac.ch[j][c]]=min(dp[i][ac.ch[j][c]],dp[i-1][j]+(ac.mp[s[i-1]]!=c)); } } } } int main(){ int n; int kase=0; while(scanf("%d",&n)!=EOF&&n){ ac.init(); for(int i=0;i<n;i++){ scanf("%s",s); ac.inser(s); } ac.getfail(); scanf("%s",s); len=strlen(s); DP(); int ans=inf; for(int i=0;i<ac.sz;i++)if(!ac.match[i]){ ans=min(dp[len][i],ans); } if(ans==inf) ans=-1; printf("Case %d: %d\n",++kase,ans); } return 0; }



