博弈论
https://blog.csdn.net/lgdblue/article/details/15809893
(一)巴什博奕(Bash Game):只有一堆n个物品,两个人轮流从这堆物品中取物,规
定每次至少取一个,最多取m个。最后取光者得胜。
显然,如果n=m+1,那么由于一次最多只能取m个,所以,无论先取者拿走多少个,
后取者都能够一次拿走剩余的物品,后者取胜。因此我们发现了如何取胜的法则:如果
n=(m+1)r+s,(r为任意自然数,s≤m),那么先取者要拿走s个物品,如果后取者拿走
k(≤m)个,那么先取者再拿走m+1-k个,结果剩下(m+1)(r-1)个,以后保持这样的
取法,那么先取者肯定获胜。总之,要保持给对手留下(m+1)的倍数,就能最后获胜。
这个游戏还可以有一种变相的玩法:两个人轮流报数,每次至少报一个,最多报十
个,谁能报到100者胜。
(二)威佐夫博奕(Wythoff Game):有两堆各若干个物品,两个人轮流从某一堆或同
时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
这道题是威佐夫博弈的一道入门题,问的十分简单,就是套威佐夫博弈的两个公式即可,因此顺带说说威佐夫博弈,威佐夫博弈和巴什博奕的场景很类似,所以索性就套用我在巴什博奕那篇文章中所描述的的那个场景。有两个二货,比赛拿XX(XX可以是任何东西,只要能定量拿走就好),只是这一次他们不再将XX混为一堆,而是作为两堆(两堆XX的数量均任意个),然后拿走的方式也改为: 1,从一堆里拿,可以拿任意数量个。2,从两堆里分别拿相等数量个。这两种方式二选一,但至少拿走一个XX,若谁取走最后一个XX,谁就赢了。是不是场景变得比巴什博奕麻烦了那么一丢丢啊~~~~
那么问题来了,如何取胜呢,,,(以下论述均是我参考了百度百科上的论述所写的,如果大家觉得写的太难看,可以直接参照百度百科上的:威佐夫博弈)
首先,我们标记一下这两堆石头:(a,b),其中a表示当前状态第一堆的数量,b表示当前状态第二堆的数量,(这里我要强调一点:就是这两堆XX它们的价值是等价的,它们是可以互换的,并不一定说第二堆的数量一定比第一堆多,这一点在后续论述中是有一定作用的)。
然后百科上对于(a,b)也给了一个特定的名称叫做“局势”,然后给出一些明显的必败状态(也就是当你面对这些状态时,只要你的对手够聪明,不犯错,无论你怎么拿,你都是必输的)(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)、...... 、(ak,bk) (k = 0, 1, 2, 3,......)。并称这些必败状态为“奇异局势”(至于为什么要叫奇异局势......额......不太清楚,忽略吧~)接下来的工作就是找出这些奇异局势的特点并总结规律。
然后就会得到a0=b0=0,ak是未在前面出现过的最小自然数,而 bk= ak + k。然后公式化就得到了奇异局势的状态公式:
ak = [ k * (1 + √5) / 2 ] , ([x]表示对x取整,也就是 (int)x )
bk = ak + k
按百科上所说,奇异局势有三个性质——
性质1:每个自然数都包含在且只包含在一个奇异局势中。
证明:因为ak为在其之前的奇异局势中未出现过的最小的自然数,所以ak的取值一直是保证在之前状态未出现过的数中的最小值,所以每一个当前状态的ak都要比之前的状态的ak要大,即ak>ak-1(k-1是下标),还想不通。。。不要紧,,把k和k-1带入上面ak的公式,这总能接受吧~~~~但ak不一定比bk-1大,看上面给出的几组奇异局势就不难看出。又bk=ak+k>ak-1+(k-1)=bk-1,所以对于任意的奇异状态(ak,bk)之前的状态中一定未出现过其中的数字,但ak取值是自动取当前未出现过的最小的数字,所以每一个自然数都一定会出现,故性质得证。
性质2:对任意的奇异局势,任何合法的操作都会使其成为非奇异局势,也就是奇异局势的所有后继状态均为非奇异局势。
证明:①若只从一堆里取XX,那么另一堆得数量没变,由性质1知,这个没变的自然数只会出现在当前的奇异局势中,所以当另一堆发生变化时,改变后得到的状态一定是非奇异局势。
②若从两堆里取相同数量的XX,那么由于 bk - ak = k (由公式得),所以他们之间的差值是不会变的,又因为对于任意的奇异局势它的两堆之间的差值是唯一值k,所以这种取法后的状态仍旧是非奇异局势。故性质得证。
性质3:任何非奇异局势都可以通过某种合法操作得到奇异局势,即奇异局势的所有后继状态中存在奇异局势。
证明:对于任意的一个非奇异局势(x,y),由性质1知:任何自然数均会出现在一个奇异局势中,所以要么 x = ak,要么 y = bk (k ∈ { 0, 1, 2, 3, 4, 5, .......}),所以分类讨论:
①若x = ak,y > bk,那么y减去(y - bk)即可得到奇异局势(ak , bk).
②若x = ak,y < bk,那么两堆同时减掉x-a(y-x) (y-x为下标),得到奇异局势(a(y-x) , a(y-x)+y-x).
③若x > ak,y = bk,那么x减去(x - ak)即可得到奇异局势(ak , bk).
④若x < ak,y = bk,这时又要对该状况细化分类讨论:
情况(1): x = aj , (j < k),此时从y中拿走(y - bj)即可得到奇异局势(aj , bj),
情况(2): x = bj , (j < k),此时从y中拿走(y - aj)即可得到奇异局势(aj , bj).
这里的④为什么要分类呢?这就要注意上文中我曾提到的强调点,这两堆是等价值的,也就是情况(2)得到奇异局势其实是(bj , aj),此时第一堆是比第二堆多的,为了同意奇异局势的格式才把它写成(aj , bj)。所以细化分类讨论的其实是对操作后 第一堆多余第二堆 和 第二堆多余第一堆 的两种情况进行讨论。这样性质3也得证。
有两堆物品分别为(an, bn)。两个人轮流取,至少取一个,有两种取法,取到最后一个者胜利。
1.从任意一堆中取任意个 > 1。
2.从两堆中取同样多个。
结论:
对于任意的局势(a, b)(a < b),必败点为(b-a) * (sqrt(5)+1)/2 = a.
证明:
第一个必败点为(0, 0),即谁面对当前局势必输。
第二个必败点为(1, 2),无论先手怎么取,后手都可以通过一步将局势转为(0, 0)。
第三个必败点为(3, 5),后手总可以通过一步转为(0, 0)或者(1, 2)。
接下来的必败点为(4, 7), (6, 10), (8, 13)··· ···
总结规律:
1.对于任何一个必败点局势(a, b),a都为之前未出现的最小整数.
2.必败点的差值满足等差数列0,1,2,3,4,5··· ···
3.对于每个必败点,a = (int)(b-a)*(sqrt(5) + 1)/2。((sqrt(5) + 1)/2为1.618, 0.618为黄金分割)
性质:
任何非必败点都可以通过一步适当操作转化为必败点。
1.a=b,同时拿走a,剩下(0, 0)
2.a<b,两种方法:
1)同时拿,差不变。所以同时拿走a - (b-a)*1.618个后转为必败点。(前提a > (b-a)*1.618)
2)只拿一个的情况。遍历0-b枚举差值,找a-i和b或者b-i和a满足条件的局势即可。
例题:
Problem Description
有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法,一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目,如果轮到你先取,假设双方都采取最好的策略,问最后你是胜者还是败者。
Input
输入包含若干行,表示若干种石子的初始情况,其中每一行包含两个非负整数a和b,表示两堆石子的数目,a和b都不大于1,000,000,000。
Output
输出对应也有若干行,每行包含一个数字1或0,如果最后你是胜者,则为1,反之,则为0。
Sample Input
2 1 8 4 4 7
Sample Output
0 1 0
直接看是不是奇异局势,如果是则先手输,如果不是则先手赢
奇异局势判断a = (1+根号5)*a。
#include<iostream> #include<cstring> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; int main() { //freopen("in.in","r",stdin); //freopen("out.out","w",stdout); int n, m; while(scanf("%d%d",&n,&m)!=EOF) { int a=min(n,m); int b=max(n,m); double k=(double)b-a; int term=(int)(k*(1+sqrt(5))/2); if(term==a) printf("0\n"); else printf("1\n"); } return 0; }
https://blog.csdn.net/qq_26122039/article/details/51027722 威左夫博弈,输出方案。
#include <iostream> #include <algorithm> #include <cstring> #include <cmath> #include <vector> #include <cstdio> #define maxn 1000005 using namespace std; int pl[maxn], pr[maxn]; double t; void Init(){ t = (sqrt(5) + 1) / 2.0; for(int i = 0; i * t + i < maxn; i++){ int fa = i * t; pl[fa] = i; pr[fa+i] = i; } } int main(){ //freopen("in.txt", "r", stdin); memset(pl, -1, sizeof(pl)); memset(pr, -1, sizeof(pr)); Init(); int a, b; while(cin >> a >> b){ if(a == 0 && b == 0) break; if(a > b) swap(a, b); int d = b - a; int h = d * t; if(h == a){ cout << 0 << endl; } else{ cout << 1 << endl; if(h < a) cout << h << " " << b - (a - h) << endl; if(pl[a] != -1 && b > a + pl[a]) cout << a << " " << a + pl[a] << endl; if(pr[b] != -1 && a > b - pr[b]) cout << b - pr[b] << " " << b << endl; if(a != b && pr[a] != -1) cout << a - pr[a] << " " << a << endl; } } return 0; }
尼姆博弈
母题:有若干堆石子,每堆石子的数量是有限的,二个人依次从这些石子堆中拿取任意的石子,至少一个(不能不取),最后一个拿光石子的人胜利。
1、我们首先以一堆为例: 假设现在只有一堆石子,你的最佳选择是将所有石子全部拿走,那么你就赢了。
2、如果是两堆:假设现在有两堆石子且数量不相同,那么你的最佳选择是取走多的那堆石子中多出来的那几个,使得两堆石子数量相同,这样,不管另一个怎么取,你都可以在另一堆中和他取相同的个数,这样的局面你就是必胜。比如有两堆石子,第一堆有3个,第二堆有5个,这时候你要拿走第二堆的三个,然后两堆就都变成了3个,这时你的对手无论怎么操作,你都可以“学”他,比如他在第一堆拿走两个,你就在第二堆拿走两个,这样你就是稳赢的
3、如果是三堆 ,我们用(a,b,c)表示某种局势,首先(0,0,0)显然是奇异局势,无论谁面对奇异局势,都必然失败。第二种奇异局势是(0,n,n),只要与对手拿走一样多的物品,最后都将导致(0,0,0)。仔细分析一
下,(1,2,3)也是奇异局势,无论对手如何拿,接下来都可以变为(0,n,n)的情型。
从中我们要明白两个理论:
一个状态是必败状态当且仅当它的所有后继都是必胜状态
一个状态是必胜状态当且仅当它至少有一个后继是必败状态
有了这两个规则,就可以用递推的方法判断整个状态图的每一个结点都是必胜还是必败状态。
这里引入L . Bouton在1902年给出的定理:状态(x1,x2,x3)为必败状态当且仅当x1 XOR x2 XOR x3=0,这里的XOR是二进制的逐位异或操作,也成Nim和。
也就是当Nim和!= 0时,先手胜利,否则失败
计算机算法里面有一种叫做按位模2加,也叫做异或的运算,我们用符号(+)表示这种运算。这种运算和一般加法不同的一点是1+1=0。先看(1,2,3)的按位模2加的结果:
1 =二进制01
2 =二进制10
3 =二进制11 (+)
———————
0 =二进制00 (注意不进位)
对于奇异局势(0,n,n)也一样,结果也是0。
任何奇异局势(a,b,c)都有a(+)b(+)c =0。
如果我们面对的是一个非奇异局势(a,b,c),要如何变为奇异局势呢?假设 a < b< c,我们只要将 c 变为 a(+)b,即可,因为有如下的运算结果: a(+)b(+)(a(+)b)=(a(+)a)(+)(b(+)b)=0(+)0=0。要将c 变为a(+)b,只要从 c中减去 c-(a(+)b)即可。也就是取走(a(+)b)个石子。这里我们要了解异或运算的一个特点 a(+)c(+)c = a
例1。(14,21,39),14(+)21=27,39-27=12,所以从39中拿走12个物体即可达到奇异局势(14,21,27)。
例2。(55,81,121),55(+)81=102,121-102=19,所以从121中拿走19个物品就形成了奇异局势(55,81,102)。
例3。(29,45,58),29(+)45=48,58-48=10,从58中拿走10个,变为(29,45,48)。
例4。我们来实际进行一盘比赛看看:
甲:(7,8,9)->(1,8,9)奇异局势
乙:(1,8,9)->(1,8,4)
甲:(1,8,4)->(1,5,4)奇异局势
乙:(1,5,4)->(1,4,4)
甲:(1,4,4)->(0,4,4)奇异局势
乙:(0,4,4)->(0,4,2)
甲:(0.4,2)->(0,2,2)奇异局势
乙:(0,2,2)->(0,2,1)
甲:(0,2,1)->(0,1,1)奇异局势
乙:(0,1,1)->(0,1,0)
甲:(0,1,0)->(0,0,0)奇异局势
甲胜。
第一个类型:就是让其判断胜利的人,对n堆石子求异或和,根据当Nim和!= 0时,先手胜利,否则失败就能判断出来。
https://www.cnblogs.com/LadyLex/p/7260629.html
https://vjudge.net/contest/296806#problem/C
大致题意是说给一个很长的棋盘,一些地方有棋子,每个格子只能放1个棋子。每次必须要向左移动1个棋子,但不能移除棋盘,也不能超过它左边的第一个棋子。求先手是否必胜。
题解:
(检查草稿箱突然发现自己有暑假的博客没发出来,尴尬......)
这道题上来硬想肯定什么都想不出来。
我们只能通过由浅入深的推理才能做出这道题。
首先我们考虑必败状态的定义:
对于某两个棋子,如果他们两个靠在了一起,那么它们对应的状态就是一个必败状态。
这一点很显然,如果两个棋子贴在一起,先手只能移动前面的棋子,而后手可以通过紧跟先手来继续使先手拿到必败状态。
那么这样,命题得证,这两个紧贴的石子就是一个必败状态了。
那么我们考虑它是从哪里转移而来的:两个棋子如果没有距离了,那么它肯定是从一开始有距离的游戏状态转移过来的.
那么我们可以得到一些式子:
sg(距离为1)=mex(sg(距离为0))=1,
sg(距离为2)=mex(sg(距离为0),sg(距离为1))=2,
sg(距离为3)=mex(sg(距离为0),sg(距离为1),sg(距离为2))=3.......
到这里,读者应该想到了什么了:这就是一个nim游戏的变种!
因此,我们把2个棋子看做1组,之间的空位数看做一堆石子,最后按照nim游戏计算即可
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn = 1e5 + 5;; int a[maxn]; int n; int t; int main() { scanf("%d", &t); while(t--) { scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%d", &a[i]); sort(a + 1, a + n + 1); int j = 1; int res = 0; if(n & 1) { res = (a[1] - 1); j++; } for(; j <= n; j += 2) { res ^= (a[j + 1] - a[j] - 1); } if(res) puts("Georgia will win"); else puts("Bob will win"); } return 0; }
#include <iostream> #include <cmath> #include <algorithm> #include <cstring> #include <queue> #include <cstdio> #include <map> using namespace std; #define ll long long int int wei[1005]; int main() { int T; cin>>T; while(T--) { int n; cin>>n; for(int i=1;i<=n;i++) cin>>wei[i]; sort(wei+1,wei+1+n); int sum=0; int i; wei[0]=0; for(i=n;i>0;i-=2) //直接从尾开始异或。 { sum^=(wei[i]-wei[i-1]-1); } if(sum) cout<<"Georgia will win\n"; else cout<<"Bob will win\n"; } }
这种阶梯博弈可以直接从n与n-1之间的距离开始异或,相继减2.
阶梯博弈
https://blog.csdn.net/u012659423/article/details/21253211 蓝桥杯高僧斗法,阶梯博弈的变形
首先是对阶梯博弈的阐述...博弈在一列阶梯上进行...每个阶梯上放着自然数个点..两个人进行阶梯博弈...每一步则是将一个集体上的若干个点( >=1 )移到前面去..最后没有点可以移动的人输.
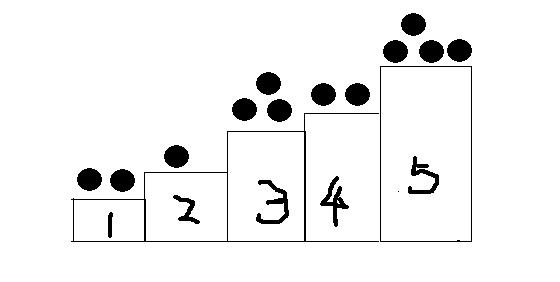
如这就是一个阶梯博弈的初始状态 2 1 3 2 4 ... 只能把后面的点往前面放...如何来分析这个问题呢...其实阶梯博弈经过转换可以变为Nim..把所有奇数阶梯看成N堆石子..做nim..把石子从奇数堆移动到偶数堆可以理解为拿走石子..就相当于几个奇数堆的石子在做Nim..( 如所给样例..2^3^4=5 不为零所以先手必败)为什么可以这样来转化?
假设我们是先手...所给的阶梯石子状态的奇数堆做Nim先手能必胜...我就按照能赢的步骤将奇数堆的石子移动到偶数堆...如果对手也是移动奇数堆..我们继续移动奇数堆..如果对手将偶数堆的石子移动到了奇数堆..那么我们紧接着将对手所移动的这么多石子从那个奇数堆移动到下面的偶数堆...两次操作后...相当于偶数堆的石子向下移动了几个..而奇数堆依然是原来的样子...即为必胜的状态...就算后手一直在移动偶数堆的石子到奇数堆..我们就一直跟着他将石子继续往下移..保持奇数堆不变...如此做下去..我可以跟着后手把偶数堆的石子移动到0..然后你就不能移动这些石子了...所以整个过程..将偶数堆移动到奇数堆不会影响奇数堆做Nim博弈的过程..整个过程可以抽象为奇数堆的Nim博弈...
其他的情况...先手必输的...类似推理...只要判断奇数堆做Nim博弈的情况即可...
为什么是只对奇数堆做Nim就可以...而不是偶数堆呢?...因为如果是对偶数堆做Nim...对手移动奇数堆的石子到偶数堆..我们跟着移动这些石子到下一个奇数堆...那么最后是对手把这些石子移动到了0..我们不能继续跟着移动...就只能去破坏原有的Nim而导致胜负关系的不确定...所以只要对奇数堆做Nim判断即可知道胜负情况...
第二个类型:先取完者判输,统计一下所有数一下大于1的个数,并将所有数字异或一遍,若大于1的个数为0&&异或和为0||大于1的个数大于0&&异或和不为零,则先手胜,否则后手胜。
经典的Nim博弈的一点变形。设糖果数为1的叫孤独堆,糖果数大于1的叫充裕堆,设状态S0:a1^a2^..an!=0&&充裕堆=0,则先手必败(奇数个为1的堆,先手必败)。S1:充裕堆=1,则先手必胜(若剩下的n-1个孤独堆个数为奇数个,那么将那个充裕堆全部拿掉,否则将那个充裕堆拿得只剩一个,这样的话先手必胜)。T0:a1^a2^..an=0&&充裕堆=0,先手必胜(只有偶数个孤独堆,先手必胜)。S2:a1^a2^..an!=0&&充裕堆>=2。T2:a1^a2^..an=0&&充裕堆>=2。这样的话我们用S0,S1,S2,T0,T2将所有状态全部表示出来了,并且S0先手必败,S1、T0先手必胜,那么我们只需要对S2和T2的状态进行分析就行了。(a)S2可以取一次变为T2。(b)T2取一次可变为S2或者S1。因为S1是先手必胜态,那么根据a,b这两个转换规则,我们就能得知S2也是先手必胜,T2是先手必败。
#include<bits/stdc++.h> using namespace std; int main() { int n; while(~scanf("%d",&n)) { int ans=0,ai,num=0; for(int i=0;i<n;i++) { scanf("%d",&ai); ans^=ai; if(ai>1)num=1; } if(num) { if(ans==0)printf("No\n"); else printf("Yes\n"); } else { if(ans==0)printf("Yes\n"); else printf("No\n"); } } return 0; }
https://blog.csdn.net/lttree/article/details/24874819
第三个类型:限制最多取的个数,例如第i堆石子共有m个,最多取r个,先对m=m%(r+1);然后在进行异或求和。再根据异或和判断输赢。
第四种类型:先手的人想赢,第一步有多少种选择。当先手必输时,很显然是0。如果先手赢,那么先手必须努力创造奇异局势,即让其剩余的石子量异或和为0,上面已经讲了当面对非奇异局势是如何转化成奇异局势。当nim游戏的某个位置:(x1,x2,x3),当且仅当其各部分的nim - sum = 0(即x1(+)x2(+)x3 = 0(也就是各部分的异或为0)) 当前位置为必败点,这对于多个堆的情况同样适用。我们首先求出所有堆异或后的值sum,再用这个值去对每一个堆进行异或,令res = x1(+)sum(sum为所有堆的异或和)。如果res < x1的话,当前玩家就从x1中取走(x1-res)个,使x1乘下res这样必然导致所有的堆的异或值为0,也就是必败点(达到奇异局势),这就是一种方案。遍历每一个堆,进行上面的断判就可以得到总的方案数。
res = x1(+)sum;其实就是除了x1之外的n-1堆异或和,a(+)b(+)c=sum;sum(+)c=a(+)b(+)c(+)c=a(+)b;
ps:注意一个必败点不可能导致另一个必败点,因为如果这样的话当前这个必败点就不是必败点了,所以这里对于每个堆的操作至多只有一种方法
可以导败必败点,如果res > x1的话就无论从这个堆取走多少都不可能导致必败点!!!
sg函数(重点!!!!!!!!!!!!!!)
g(x)=mex{ g(y) | y是x的后继}。
Sprague-Grudy定理:
令N = {0, 1, 2, 3, ...} 为自然数的集合。Sprague-Grundy 函数给游戏中的每个状态分配了一个自然数。结点v的Grundy值等于没有在v的后继的Grundy值中出现的最小自然数.
形式上:给定一个有限子集 S ⊂ N,令mex S(最小排斥值)为没有出现在S中的最小自然数。定义mex(minimal excludant)运算,这是施加于一个集合的运算,表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。
对于一个给定的有向无环图,定义关于图的每个顶点的Sprague-Garundy函数g如下:g(x)=mex{ g(y) | y是x的后继 }。
5、性质:
(1)所有的终结点所对应的顶点,其SG值为0,因为它的后继集合是空集——所有终结点是必败点(P点)。
(2)对于一个g(x)=0的顶点x,它的所有后继y都满足g(y)!=0——无论如何操作,从必败点(P点)都只能进入必胜点(N点)//对手走完又只能把N留给我们。
(3)对于一个g(x)!=0的顶点,必定存在一个后继点y满足g(y)=0——从任何必胜点(N点)操作,至少有一种方法可以进入必败点(P点)//就是那种我们要走的方法。
6、应用:
(1)可选步数为1-m的连续整数,直接取模即可,SG(x) = x % (m+1);
(2)可选步数为任意步,SG(x) = x;
(3)可选步数为一系列不连续的数,用mex(计算每个节点的值)
无论那种dfs还是打表,在预处理的过程中都需要有一种意识就是,当你想算一个点的sg函数值时,必须要准确的判断出该点所有的后继情况
https://blog.csdn.net/strangedbly/article/category/6179507 讲sg函数的。
解题模型:
1.把原游戏分解成多个独立的子游戏,则原游戏的SG函数值是它的所有子游戏的SG函数值的异或。
即sg(G)=sg(G1)^sg(G2)^...^sg(Gn)。
2.分别考虑没一个子游戏,计算其SG值。
SG值的计算方法:(重点)
1.可选步数为1~m的连续整数,直接取模即可,SG(x) = x % (m+1);
2.可选步数为任意步,SG(x) = x;
3.可选步数为一系列不连续的数,用模板计算。
模板1:打表
https://www.cnblogs.com/Ritchie/p/5396893.html 一道打表求sg函数的题,数据很多的话一般是打表找规律。
https://blog.csdn.net/qq_40932661/article/details/84968068 较难
https://blog.csdn.net/LiWen_7/article/details/7943258 较难
https://blog.csdn.net/yang_7_46/article/details/9771347 递归
//f[]:可以取走的石子个数 //sg[]:0~n的SG函数值 //hash[]:mex{} int f[N],sg[N],hash[N]; void getSG(int n) { int i,j; memset(sg,0,sizeof(sg)); for(i=1;i<=n;i++) { memset(hash,0,sizeof(hash)); for(j=1;f[j]<=i;j++) hash[sg[i-f[j]]]=1; for(j=0;j<=n;j++) //求mes{}中未出现的最小的非负整数 { if(hash[j]==0) { sg[i]=j; break; } } } }
dfs方法
//注意 S数组要按从小到大排序 SG函数要初始化为-1 对于每个集合只需初始化1遍 //n是集合s的大小 S[i]是定义的特殊取法规则的数组 int s[110],sg[10010],n; int SG_dfs(int x) { int i; if(sg[x]!=-1) return sg[x]; bool vis[110]; memset(vis,0,sizeof(vis)); for(i=0;i<n;i++) { if(x>=s[i]) { SG_dfs(x-s[i]); vis[sg[x-s[i]]]=1;
//或者直接vis[SG_dfs(x - s[i])] = 1;一个意思。 } } int e; for(i=0;;i++) if(!vis[i]) { e=i; break; } return sg[x]=e; }
一个dp+博弈论+搜索的题
https://cn.vjudge.net/contest/296806#problem/H
题意:一个有n个结点的环,第一个结点上是黑洞,其他为行星。现在有一个怪物可能在任意的行星上。甲乙两人可以顺时针驱赶怪物。甲每次可驱赶s11,s12,s13...s11,s12,s13...个格子,共k1个可能。乙每次可驱赶s21,s22,s23...s21,s22,s23...个格子,共k2种可能。谁把怪物刚好驱逐到黑洞里就赢。现在求:当怪物在第i个行星,甲(或乙)第一个驱赶时,甲(或乙)一定赢、一定输还是平局?
对于每个点都有两种状态,a推到这里和b推到这里,我们可以知道,对于1这个位置,无论哪个人在面临这样的局面时,都是必败态,我们从这个点出发,如果这个点是必败态(0),那么对于所有能一步走到这个点的位置,都有必胜态;对于每个状态,只有当它的后续状态都为1时,这个点为必败态,所以我们可以从1出发,对于每个能走到这个点的状态本身进行一个数量的统计,如果这个num=它的可操作步数,就说明这个点为必败态。
我们可以通过bfs来解决。
#include <bits/stdc++.h> using namespace std; const double eps = 1e-6; const double pi = acos(-1.0); const int INF = 0x3f3f3f3f; const int MOD = 1000000007; #define ll long long #define CL(a) memset(a,0,sizeof(a)) #define maxn 7010 #define mod 2520 int dp[2][maxn],num[2][maxn]; int n; vector<int> v[2]; void bfs() { queue<pair<int,int> > que; que.push(make_pair(0,0)); que.push(make_pair(1,0)); while(!que.empty()) { int p=que.front().first; int pos=que.front().second; int x=dp[p][pos]; que.pop(); if(x==0) { for(int i=0; i<v[!p].size(); i++) { int nxt=(pos-v[!p][i]+n)%n; if(dp[!p][nxt]==-1) { dp[!p][nxt]=1; que.push(make_pair(!p,nxt)); } } } else { for(int i=0; i<v[!p].size(); i++) { int nxt=(pos-v[!p][i]+n)%n; if(dp[!p][nxt]!=-1) continue; if(num[!p][nxt]<v[!p].size()) num[!p][nxt]++; if(num[!p][nxt]==v[!p].size()) { dp[!p][nxt]=0; que.push(make_pair(!p,nxt)); } } } } } int main () { memset(dp,-1,sizeof(dp)); memset(num,0,sizeof(num)); cin>>n; for(int i=0; i<2; i++) { int k; cin>>k; for(int j=0; j<k; j++) { int m; cin>>m; v[i].push_back(m); } } dp[0][0]=dp[1][0]=0; bfs(); for(int i=0; i<2; i++) { for(int j=1; j<n; j++) { if(dp[i][j]==0) cout<<"Lose"<<' '; else if(dp[i][j]==1) cout<<"Win"<<' '; else cout<<"Loop"<<' '; } cout<<endl; } return 0; }
一般的翻硬币游戏的规则是这样的:
N 枚硬币排成一排,有的正面朝上,有的反面朝上。我们从左开始对硬币按1 到N 编号。
第一,游戏者根据某些约束翻硬币,但他所翻动的硬币中,最右边那个硬币的必须是从正面翻到反面。例如,只能翻3个硬币的情况,那么第三个硬币必须是从正面翻到反面。如果局面是正正反,那就不能翻硬币了,因为第三个是反的。
第二,谁不能翻谁输。
有这样的结论:局面的SG 值为局面中每个正面朝上的棋子单一存在时的SG 值的异或和。即一个有k个硬币朝上,朝上硬币位置分布在的翻硬币游戏中,SG值是等于k个独立的开始时只有一个硬币朝上的翻硬币游戏的SG值异或和。比如THHTTH这个游戏中,2号、3号、6号位是朝上的,它等价于TH、TTH、TTTTTH三个游戏和,即sg[THHTTH]=sg[TH]^sg[TTH]^sg[TTTTTH].我们的重点就可以放在单个硬币朝上时的SG值的求法。
约束条件一:每次只能翻一个硬币。
一般规则中,所翻硬币的最右边必须是从正面翻到反面,因为这题是只能翻一个硬币,那么这个硬币就是最右边的硬币,所以,每次操作是挑选一个正面的硬币翻成背面。
对于任意一个正面的硬币,SG值为1。
有奇数个正面硬币,局面的SG值==1,先手必胜,有偶数个正面硬币,局面的SG值==0,先手必败。
约束条件二:每次能翻转一个或两个硬币。(不用连续)
每个硬币的SG值为它的编号,初始编号为0,与NIM游戏是一样的。
如果对于一个局面,把正面硬币的SG值异或起来不等于0,既a1^a2^a3^…^an==x,对于an来说一定有an'=an^x<an。
如果an'==0,意思就是说,把an这个值从式子中去掉就可以了。对应游戏,就是把编号为an的正面硬币翻成背面就可以了。因为an^x==0,而a1^a2^a3^…^an==x,即an^a1^a2^a3^…^an==0,即a1^a2^a3^…^an-1==0,只要在原来的x里面去掉an就可以了。
如果an'!=0,意思就是说,把an这个值从式子中去掉后再在式子中加上an',an'<an。对应游戏,去掉an就是把编号为an的正面硬币翻成背面,加上an',如果编号为an'的硬币是正面,我们就把它翻成背面,是背面就翻成正面,总之,就是翻转编号为an'的硬币。因为an^x!=0,所以an^a1^a2^a3^…^an!=0,即a1^a2^a3^…^an-1!=0,而这里的
an'=a1^a2^a3^…^an-1,所以在x中去掉an后,要对an'进行异或,也就是翻转,正转反,反转正。
约束条件三:每次必须连续翻转k个硬币。
我们以k==3为例。
我们计算的是个数为N的硬币中,其中最后一个硬币为正面朝上,的sg值。
当N==1时,硬币为:正,先手必输,所以sg[1]=0。
当N==2时,硬币为:反正,先手必输,所以sg[2]=0。
当N==3时,硬币为:反反正,先手必胜,所以sg[3]=1。
当N==4时,硬币为:反反反正,先手操作后为:反正正反,子状态局面的SG=0^1=1,那么sg[4]=0。
当N==5时,硬币为:反反反反正,先手操作后为:反反正正反,子状态局面的SG=1^0=1,那么sg[5]=0。
当N==6时,硬币为:反反反反反正,先手操作后为:反反反正正反,子状态局面的SG=0^0=0,那么sg[6]=1。
根据观察,可以知道,从编号为1开始,sg值为:001 001 001 001……
根据观察,可以知道,sg的形式为000…01 000…01,其中一小段0的个数为k-1。
约束条件4:每次翻动一个硬币后,必须翻动其左侧最近三个硬币中的一个,即翻动第x个硬币后,必须选择x-1,x-2,x-3中的其中一个硬币进行翻动,除非x是小于等于3的。(Subtraction Games)
当N==1时,硬币为:正,先手必赢,所以sg[1]=1。
当N==2时,硬币为:反正,先手必赢,因为先手可以翻成反反或正反,可能性为2,所以sg[2]==2。
当N==3时,硬币为:反反正,先手操作后可以为:反正
位置x:1 2 3 4 5 6 7 8 9 10 11 12 13 14...
sg[x]: 1 2 3 0 1 2 3 0 1 2 3 0 1 2…
这个与每次最多只能取3个石子的取石子游戏的SG分布一样,同样还有相似的这类游戏,约束条件5也是一样。
约束条件5:每次必须翻动两个硬币,而且这两个硬币的距离要在可行集S={1,2,3}中,硬币序号从0开始。(Twins游戏)
当N==1时,硬币为:正,先手必输,所以sg[0]=0。
当N==2时,硬币为:反正,先手必赢,所以sg[1]=1。
当N==3时,硬币为:反反正,先手必赢,所以sg[2]=2。
当N==4时,硬币为:反反反正,先手必赢,所以sg[3]=3。
当N==5时,硬币为:反反反反正,先手必输,所以sg[4]=0。
位置x:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14...
sg[x]: 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2…
约束条件6:每次可以翻动一个、二个或三个硬币。(Mock Turtles游戏)
初始编号从0开始。
当N==1时,硬币为:正,先手必胜,所以sg[0]=1.
当N==2时,硬币为:反正,先手必赢,先手操作后可能为:反反或正反,方案数为2,所以sg[1]=2。
当N==3时,硬币为:反反正,先手必赢,先手操作后可能为:反反反、反正反、正反正、正正反,方案数为4,所以sg[2]=4。
位置x:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14...
sg[x]: 1 2 4 7 8 11 13 14 16 19 21 22 25 26 28…
看上去sg值为2x或者2x+1。我们称一个非负整数为odious,当且仅当该数的二进制形式的1出现的次数是奇数,否则称作evil。所以1,2,4,7是odious因为它们的二进制形式是1,10,100,111.而0,3,5,6是evil,因为它们的二进制形式是0,11,101,110。而上面那个表中,貌似sg值都是odious数。所以当2x为odious时,sg值是2x,当2x是evil时,sg值是2x+1.
这样怎么证明呢?我们会发现发现,
evil^evil=odious^odious=evil
evil^odious=odious^evil=odious
假设刚才的假说是成立的,我们想证明下一个sg值为下一个odious数。注意到我们总能够在第x位置翻转硬币到达sg为0的情况;通过翻转第x位置的硬币和两个其它硬币,我们可以移动到所有较小的evil数,因为每个非零的evil数都可以由两个odious数异或得到;但是我们不能移动到下一个odious数,因为任何两个odious数的异或都是evil数。
假设在一个Mock Turtles游戏中的首正硬币位置x1,x2,…,xn是个P局面,即sg[x1]^…^sg[xn]=0.那么无可置疑的是n必定是偶数,因为奇数个odious数的异或是odious数,不可能等于0。而由上面可知sg[x]是2x或者2x+1,sg[x]又是偶数个,那么x1^x2^…^xn=0。相反,如果x1^x2^…^xn=0且n是偶数,那么sg[x1]^…^sg[xn]=0。这个如果不太理解的话,我们可以先这么看下。2x在二进制当中相当于把x全部左移一位,然后补零,比如说2的二进制是10,那么4的二进制就是100。而2x+1在二进制当中相当于把x全部左移一位,然后补1,比如说2的二进制是10,5的二进制是101。现在看下sg[x1]^…^sg[xn]=0,因为sg[x]是2x或者2x+1,所以式子中的2x+1必须是偶数个(因为2x的最后一位都是0,2x+1的最后一位都是1,要最后异或为0,2x+1必须出现偶数次)。实际上的情况可能是这样的:

MT游戏当中的P局面是拥有偶数堆石子的Nim游戏的P局面。
#include<iostream> #include<cstdio> #include<ctime> #include<cstring> #include<cmath> #include<algorithm> #include<cstdlib> #include<vector> #define C 240 #define TIME 10 #define inf 1<<25 #define LL long long using namespace std; int main(){ int n,a[100]; while(scanf("%d",&n)!=EOF){ int ret=0,k; if(n==0){ puts("Yes"); continue; } for(int i=0;i<n;i++) scanf("%d",&a[i]); sort(a,a+n); int len=1; for(int i=1;i<n;i++) if(a[i]!=a[len-1]) a[len++]=a[i]; for(int i=0;i<len;i++){ int k=a[i]; int cnt=0,t=2*k; while(k){ if(k&1) cnt++; k>>=1; } if(cnt%2==0) ret^=t+1; else ret^=t; } puts(ret?"No":"Yes"); } return 0; }
约束条件7:每次可以连续翻动任意个硬币,至少翻一个。(Ruler游戏)
初始编号从1开始。
那么这个游戏的SG函数是g(n)=mex{0,g(n-1),g(n-1)^g(n-2),…,g(n-1)^…^g(1)}
根据SG函数可以得到SG值表如下。
位置x:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
g(x): 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16…
所以sg值为x的因数当中2的能达到的最大次幂。比如14=2*7,最大1次幂,即2;16=2*2*2*2,最大4次幂,即16。
这个游戏成为尺子游戏是因为SG函数很像尺子上的刻度。
约束条件8:每次必须翻转4个对称的硬币,最左与最右的硬币都必须是从正翻到反。(开始的时候两端都是正面)(Grunt游戏)
这是Grundy游戏的变种,初始编号从0开始。
当首正硬币位置为0,1,2时是terminal局面,即 终结局面,sg值都是0。当首正硬币位置n大于等于3的时候的局面可以通过翻0,x,n-x,n四个位置得到(其中x<n/2可保证胜利)。
这就像是把一堆石子分成两堆不同大小石子的游戏,也就是Grundy游戏。
附注:
参考资料http://blog.sina.com.cn/s/blog_51cea4040100h3wl.html
部分内容还是《Game Theory》翻译过来的
//HDOJ 4155 The Game of 31 博弈搜索 /* 题意:有编号为1、2、3、4、5、6的牌各4张,共24张,两个人轮流取牌, 取牌后要使所有取出的牌的总不超过31,不能取的输。 游戏从给定的局面开始。 思路:从给定的局面开始dfs,当此状态能够到达p状态,则此状态有n状态 否则为p状态,然后判断此时是先手还是后手 */ #include<stdio.h> #include<string.h> #include<stdlib.h> #define N 100 #define M 10 char str[N]; int num[M]; int len,sum; void init(){ int i; for(i = 1; i <= 6; ++i) num[i] = 4; len = strlen(str); sum = 0; for(i = 0; i < len; ++i){ --num[str[i]-'0']; sum += str[i]-'0'; } } bool dfs(int sum){ int i; if(sum > 31) return 0; for(i = 1; i <= 6; ++i){ if(num[i] && sum+i<=31){ --num[i]; if(dfs(sum+i) == 0){ ++num[i]; return 1; } ++num[i]; } } return 0; } int main(){ while(scanf("%s",&str)!=EOF){ init(); printf("%s ",str); if(dfs(sum)) puts(len%2 ? "B" : "A"); else puts(len%2 ? "A" : "B"); } return 0; }
没看懂的题:HDOJ1517&POJ2505 A Multiplication Game [K(2~9)倍博弈]
HDOJ1538 A Puzzle for Pirates [海盗分金问题]
HDOJ3404 Switch lights [Nim积]
HDOJ3389Game [找规律]
HDOJ1404 Digital Deletions [SG博弈] 可做。
HDOJ4111 Alice and Bob [SG博弈]DP+石子合并 可做
HDOJ3094 A tree game [有向无环树形图SG博弈]
树的删边游戏http://blog.csdn.net/acm_cxlove/article/details/7842586
HDOJ3590 PP and QQ [树形SG博弈]反博弈,砍树
树的删边游戏+ANTI-SG,
http://blog.csdn.net/acm_cxlove/article/details/7842743
HDOJ3197 Game [树形SG博弈]砍树



