卡特兰数 斯特林数

 

卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。

卡特兰数前几项为 : C0＝1，C1＝1，C2＝2，C3＝5，C4＝14，C5＝42，C6＝132，C7＝429，C8＝1430，C9＝4862，C10＝16796

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, 18367353072152, 69533550916004, 263747951750360, 1002242216651368, 3814986502092304, 14544636039226909, 55534064877048198, 212336130412243110, 812944042149730764, 3116285494907301262, 11959798385860453492, 45950804324621742364, ...

输入一个整数n，计算h(n)。

令h(0)=1,h(1)=1，Catalan数满足递推式：h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
例如：

h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另类递推式：h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为：h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
递推关系的另类解为：h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,...)

卡特兰数的应用
应用1：出栈次序。一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?h(n)
常规分析
首先，我们设f(n)=序列个数为n的出栈序列种数。同时，我们假定，从开始到栈第一次出到空为止，这段过程中第一个出栈的序数是k。特别地，如果栈直到整个过程结束时才空，则k=n。首次出空之前第一个出栈的序数k将1~n的序列分成两个序列，其中一个是1~k-1，序列个数为k-1，另外一个是k+1~n，序列个数是n-k。此时，我们若把k视为确定一个序数，那么根据乘法原理，f(n)的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的f(n)=f(k-1)×f(n-k)。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为：f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。看到此处，再看看卡特兰数的递推式，答案不言而喻，即为f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n+1)(n=0，1，2，……)。最后，令f(0)=1，f(1)=1。
非常规分析
对于每一个数来说，必须进栈一次、出栈一次。我们把进栈设为状态‘1’，出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b)，因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数，1的累计数不小于0的累计数的方案种数。在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描，0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时，必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数，此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换，使之成为n-m个0和n-m-1个1，结果得1个由n+1个0和n-1个1组成的2n位数，即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。反过来，任何一个由n+1个0和n-1个1组成的2n位二进制数，由于0的个数多2个，2n为偶数，故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换，使之成为由n个0和n个1组成的2n位数，即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。因而不合要求的2n位数与n+1个0，n－1个1组成的排列一一对应。
显然，不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=c(2n,n)/(n+1)=h(n)。

应用2描述：n对括号有多少种匹配方式？h(n)
       思路：n对括号相当于有2n个符号，n个左括号、n个右括号，可以设问题的解为f(2n)。第0个符号肯定为左括号，与之匹配的右括号必须为第2i+1字符。因为如果是第2i个字符，那么第0个字符与第2i个字符间包含奇数个字符，而奇数个字符是无法构成匹配的。
       通过简单分析，f(2n)可以转化如下的递推式 f(2n) = f(0)*f(2n-2) + f(2)*f(2n - 4) + ... + f(2n - 4)*f(2) + f(2n-2)*f(0)。简单解释一下，f(0) * f(2n-2)表示第0个字符与第1个字符匹配，同时剩余字符分成两个部分，一部分为0个字符，另一部分为2n-2个字符，然后对这两部分求解。f(2)*f(2n-4)表示第0个字符与第3个字符匹配，同时剩余字符分成两个部分，一部分为2个字符，另一部分为2n-4个字符。依次类推。
       假设f(0) = 1，计算一下开始几项，f(2) = 1, f(4) = 2, f(6) = 5。结合递归式，不难发现f(2n) 等于h(n)。
应用3描述：矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？h(n-1)
       思路：可以这样考虑，首先通过括号化，将P分成两个部分，然后分别对两个部分进行括号化。比如分成(a1)×(a2×a3.....×an)，然后再对(a1)和(a2×a3.....×an)分别括号化；又如分成(a1×a2)×(a3.....×an)，然后再对(a1×a2)和(a3.....×an)括号化。
       设n个矩阵的括号化方案的种数为f(n)，那么问题的解为
        f(n) = f(1)*f(n-1) + f(2)*f(n-2) + f(3)*f(n-3) + f(n-1)*f(1)。f(1)*f(n-1)表示分成(a1)×(a2×a3.....×an)两部分，然后分别括号化。
       计算开始几项，f(1) = 1, f(2) = 1, f(3) = 2, f(4) = 5。结合递归式，不难发现f(n)等于h(n-1)。
应用4描述（和应用1一样）：一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列?h(n)
       思路：这个与加括号的很相似，进栈操作相当于是左括号，而出栈操作相当于右括号。n个数的进栈次序和出栈次序构成了一个含2n个数字的序列。第0个数字肯定是进栈的数，这个数相应的出栈的数一定是第2i+1个数。因为如果是2i，那么中间包含了奇数个数，这奇数个肯定无法构成进栈出栈序列。
       设问题的解为f(2n)， 那么f(2n) = f(0)*f(2n-2) + f(2)*f(2n-4) + f(2n-2)*f(0)。f(0) * f(2n-2)表示第0个数字进栈后立即出栈，此时这个数字的进栈与出栈间包含的数字个数为0，剩余为2n-2个数。f(2)*f(2n-4)表示第0个数字进栈与出栈间包含了2个数字，相当于1 2 2 1，剩余为2n-4个数字。依次类推。
       假设f(0) = 1，计算一下开始几项，f(2) = 1, f(4) = 2, f(6) = 5。结合递归式，不难发现f(2n) 等于h(n)。
应用5描述：n个节点构成的二叉树，共有多少种情形？h(n)
       思路：可以这样考虑，根肯定会占用一个结点，那么剩余的n-1个结点可以有如下的分配方式，T(0, n-1),T(1, n-2),...T(n-1, 0)，设T(i, j)表示根的左子树含i个结点，右子树含j个结点。
       设问题的解为f(n)，那么f(n) = f(0)*f(n-1) + f(1)*f(n-2) + .......+ f(n-2)*f(1) + f(n-1)*f(0)。假设f(0) = 1，那么f(1) = 1, f(2) = 2, f(3) = 5。结合递推式，不难发现f(n)等于h(n)。
应用6描述：在圆上选择2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？h(n)
       思路：以其中一个点为基点，编号为0，然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定是奇数，否则，这两个编号间含有奇数个点，势必会有个点被孤立，即在一条线段的两侧分别有一个孤立点，从而导致两线段相交。设选中的基点为A，与它连接的点为B，那么A和B将所有点分成两个部分，一部分位于A、B的左边，另一部分位于A、B的右边。然后分别对这两部分求解即可。
       设问题的解f(n)，那么f(n) = f(0)*f(n-2) + f(2)*f(n-4) + f(4)*f(n-6) + ......f(n-4)*f(2) + f(n-2)*f(0)。f(0)*f(n-2)表示编号0的点与编号1的点相连，此时位于它们右边的点的个数为0，而位于它们左边的点为2n-2。依次类推。
       f(0) = 1, f(2) = 1, f(4) = 2。结合递归式，不难发现f(2n) 等于h(n)。
应用7描述：求一个凸多边形区域划分成三角形区域的方法数？h(n-2)
      思路：以凸多边形的一边为基，设这条边的2个顶点为A和B。从剩余顶点中选1个，可以将凸多边形分成三个部分，中间是一个三角形，左右两边分别是两个凸多边形，然后求解左右两个凸多边形。
      设问题的解f(n)，其中n表示顶点数，那么f(n) = f(2)*f(n-1) + f(3)*f(n-2) + ......f(n-2)*f(3) + f(n-1)*f(2)。f(2)*f(n-1)表示三个相邻的顶点构成一个三角形，那么另外两个部分的顶点数分别为2和n-1。
      设f(2) = 1，那么f(3) = 1, f(4) = 2, f(5) = 5。结合递推式，不难发现f(n) 等于h(n-2)。
应用8描述：有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？h(n)
     思路：可以将持5元买票视为进栈，那么持10元买票视为5元的出栈。这个问题就转化成了栈的出栈次序数。由应用2的分析直接得到结果，f(2n) 等于h(n)。

PS应用8：游乐园门票1元一张，每人限购一张。现在有10个小朋友排队购票，其中5个小朋友每人只有1元的钞票一张，另5个小朋友每人只有2元的钞票一张，售票员没有准备零钱。问：有多少种排队方法，使售票员总能找的开零钱？

答：现把拿1元的5个小朋友看成是相同的，把拿2元的5个小朋友也看成是相同的，使用我们常用的“逐点累加法”：

图中每条小横段表示拿1元的小朋友，每条小竖段表示拿2元的小朋友，要求从A走到B的过程中网格中任何点均有横段数不小于竖段数：拿1元的要先，且人数不能少于拿2元的，即不能越过对角线AB：每个点所标的数即为从A走到此点的方法数。求从A到B的走法的方法数。逐点累加可求出为42，即卡特兰数C5＝42。

 

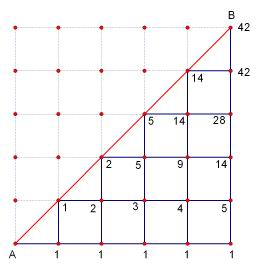
又由于每个小朋友是不相同的，所以共有42×5！×5！＝42×120×120＝604800种情况。

若把此题的10个人，拿1元的有5人，拿2元的有5人改为共有2n个人，拿1元的n人，拿2元的n人，则符合要求的排队方法数为：n!*n!*h(n)=n!*n!*C(2n,n)/(n+1)=(2n)!/(n+1)

卡特兰数的实例：
组合数学中有非常多的组合结构可以用卡塔兰数来计数。在Richard P. Stanley的Enumerative Combinatorics: Volume 2一书的习题中包括了66个相异的可由卡塔兰数表达的组合结构。以下用Cn=3和Cn=4举若干例：
例1.Cn表示长度2n的dyck word的个数。Dyck word是一个有n个X和n个Y组成的字串，且所有的前缀字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:  h(3)=5
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
例2.将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数:h(3)=5
((())) ()(()) ()()() (())() (()())
例3.Cn表示有n个节点组成不同构二叉树的方案数。下图中n等于3，圆形表示节点，月牙形表示什么都没有。h(3)=5

 

例4.Cn表示所有在n × n格点中不越过对角线的单调路径的个数。一个单调路径从格点左下角出发，在格点右上角结束，每一步均为向上或向右。计算这种路径的个数等价于计算Dyck word的个数： X代表“向右”，Y代表“向上”。下图为n = 4的情况：h(4)=14

类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？h(n)

 

 

例5.Cn表示通过连结顶点而将n边的凸多边形分成三角形的方法个数。下图中为n=6的情况：h(n-2)=h(4)=14

 

例6.Cn表示用n个长方形填充一个高度为n的阶梯状图形的方法个数。下图为 n = 4的情况:h(4)=14

 

 

例7.进栈出栈问题：
饭后，姐姐洗碗，妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗，洗前也是摞成一摞的，也许因为小妹贪玩而使碗拿进碗橱不及时，姐姐则把洗过的碗摞在旁边，问：小妹摞起的碗有多少种可能的方式？h(n)
一个汽车队在狭窄的路面上行驶，不得超车，但可以进入一个死胡同去加油，然后再插队行驶，共有n辆汽车，问共有多少种不同的方式使得车队开出城去？h(n)

 

 

https://vjudge.net/contest/284040#problem/J

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

typedef long long ll;
ll mapp[40][40];
void init() {
  for(int i = 0; i < 36; i++) mapp[i][0] = 1;
    for(int i = 1;i <= 35; i++)
        for(int j = 1; j <= i; j++)
            mapp[i][j] = mapp[i - 1][j] + mapp[i][j - 1];

}
int n;
int main() {
    init();
    int ant = 0;
    while(~scanf("%d", &n)) {
        if(n == -1) break;
        printf("%d %d %lld\n", ++ant, n, 2 * mapp[n][n]);
    }
    return 0;
}

 

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

typedef long long ll;
ll Ca[40];
void init() {
    Ca[0] = 1;
    Ca[1] = 1;
    for (int i = 2 ; i <= 35 ; i++)
        for (int j = 0 ; j <= i - 1 ; j++)
            Ca[i] += Ca[j] * Ca[i - 1 - j];
}
int n;
int main() {
    init();
    int ant = 0;
    while(~scanf("%d", &n)) {
        if(n == -1) break;
        printf("%d %d %lld\n", ++ant, n, 2 * Ca[n]);
    }
    return 0;
}

 https://blog.csdn.net/doc_sgl/article/details/8880468

https://blog.csdn.net/lishuhuakai/article/details/8034075

https://blog.csdn.net/tassardge/article/details/82926832

 

http://lanqi.org/skills/10939/  有证明 

 

hdoj2067 水题

给出一个棋盘n*n，求从左下角到右上角的不经过对角线的所有走法，这个经过分析也是卡特兰数。我们把往右走看做1，把往上走看做0，那么从左向右看做一系列的101100.。。，和那个求出栈序列的就是一个问题了，即0的个数不能超过1，由于上半角和下半角一样，所以求出来卡特兰数*2就是我们的答案了。

注：从(0,0)到(n, n)不接触对角线上的点和从(0, 0)到(n, n)不穿过对角线上的点的方法数是不同的。后者可看作n个字符的出栈序列，前者可看作在先在栈中加入一个字符，之后在最后的操作之前栈底不能为空，所以方法数为h(n - 1)。

同样可以使用对称的方法求解:

对于不能接触对角线的方法数的解法为：由于不接触对角线，那么第一步一定走向(1, 0), 倒数第二步的位置一定是(n, n - 1)。那么总的方法数为：C(n - 1, 2n-2)。之后需要减去接触对角线的方法数：如果我们从(0, 1)出发，到达(n, n -1)的路径一定会接触对角线，而这样的路径和从(1, 0)到(n, n -1)不合法的路径是一一对应的的（可以把它从最后离开对角线的点到(1, 0)做一个关于y=x的对称），那么总的方法数为2 * (C(n- 1, 2n - 2) - C(n, 2n - 2)) = 2 * h(n - 1)种方法

对于可以接触但不能穿过对角线的解法为：不能穿过y=x，等价与不能接触y=x+1，所以，从(0, 0) 到(n, n)的总方法数为C(n, 2n)，之后减去不符合要求的方法数。将(0, 0)关于y=x+1做对称可得到点(-1, 1)，从(-1, 1)到点(n, n)必定接触y=x+1，方法数为C(n - 1, 2n)。所以符合要求的方法数为：C(n, 2n) - C(n - 1,2n) = C(n, 2n) - C(n + 1,2n) = h(n)

 

 

 https://blog.csdn.net/qq_40889820/article/details/97546349 牛客一道题目ABBA，证明比较详细。证明上面结论

 https://blog.csdn.net/qq_39239844/article/details/96475068

 

https://blog.csdn.net/sxh759151483/article/details/83420939 组合数学里的

https://blog.csdn.net/qq_40507857/article/details/82866466

第一类斯特林数

第一类斯特林数 
解决问题：给n个元素，求出k个环排列的方法数 
Stirling[n][k]
1
1      1
2      3       1
6      11      6       1
24     50      35      10     1
120    274     225     85     15     1
720    1764    1624    735    175    21    1
5040   13068   13132   6769   1960   322   28   1
40320  109584  118124  67284  22449  4536  546  36  1
362880 1026576 1172700 723680 269325 63273 9450 870 45 1

 

const int maxn = 21;
ll Stirling[maxn][maxn], fac[maxn] = {1};
void init() {
    for(ll i = 1; i < maxn; i++)
        fac[i] = fac[i - 1] * i;
    Stirling[0][0] = 0;
    Stirling[1][1] = 1;
    for(ll i = 2; i < maxn; i++) {
        for(ll j = 1; j <= i; j++) {
            Stirling[i][j] = Stirling[i - 1][j - 1] + (i - 1) * Stirling[i - 1][j];
        }
    }
}

第二类斯特林数

https://blog.csdn.net/BePosit/article/details/83819295

https://vjudge.net/contest/285721#rank H题是斯特林

第二类斯特林数 
将n个不同元素拆分成m个集合的方案数（m个集合不为空）
Stirling[n][m]
1
1 1
1 3   1
1 7   6    1
1 15  25   10    1
1 31  90   65    15    1
1 63  301  350   140   21    1
1 127 966  1701  1050  266   28   1
1 255 3025 7770  6951  2646  462  36  1
1 511 9330 34105 42525 22827 5880 750 45 1

const int maxn = 21;
ll Stirling[maxn][maxn];
void init() {
    Stirling[0][0] = 0;
    Stirling[1][1] = 1;
    for(ll i = 2; i < maxn; i++) {
        for(ll j = 1; j <= i; j++) {
            Stirling[i][j] = Stirling[i - 1][j - 1] + j * Stirling[i - 1][j];
        }
    }
}

贝尔数

贝尔数
n个数可以划分成多少个集合
每个贝尔数是第二类斯特林数的和 

const int maxn = 21;
ll Bell[maxn];
void init() {
    ll T[maxn];
    Bell[0] = 1;
    Bell[1] = 1;
    T[0] = 1;
    for(int i = 2; i < maxn; i++) {
        T[i - 1] = Bell[i - 1];
        for(int j = i - 2; j >= 0; j--)
            T[j] = T[j] + T[j + 1];
        Bell[i] = T[0];
    }
}

 https://vjudge.net/contest/285721#problem/H

第二类斯特林与贝尔数的裸替