《python数据分析（第2版）-阿曼多.凡丹戈》读书笔记第10章-预测性分析与机器学习

python数据分析个人学习读书笔记-目录索引

第10章预测性分析与机器学习

 　　最近，预测性分析与机器学习已经纳入许多行业的主流数据科学和数据分析的行列。相对于其他领域而言，我们对这两个领域取得突飞猛进发展的期待要更热切一些。甚至有人预言，机器学习的发展速度将日益加快，因此，几十年内，人工就会被智能机器所替代。当然，就目前人工通用智能（AGI）的发展现状来看，这只是一个遥远的乌托邦而已；但是机器学习已经取得了长足的进步，可用于自驾车、聊天机器人和AI助手，如亚马逊的Alexa、苹果的Siri以及Ok Google。然而，目前即使是进行非常简单的判断，如判断网络图片中是否含有猫或狗等，都需要大量的运算和数据作为支撑。预测性分析则需要借助各种各样的技术，包括机器学习，才能做出有用的判断。例如，某客户是否有能力偿还其贷款，或者某位女性客户是否有孕在身。

　　为了完成这些预测，需要从海量数据中提取特征。关于特征，我们之前也曾经提到过，它们又被称为预测变量。进行预测时，特征通常用于输入变量。实质上，特征可以从数据中提取，然后要做的是，找到一个函数，将特征映射到目标上。当然，这个目标可能是已知的，也可能是未知的。寻找合适的函数很难，为此，通常需要把多种不同的算法和模型组合在一起，也就是所谓的集成。集成的输出结果可以是一组模型投票决出的结果，也可以是所有结果的一个折中。但是，我们还可以使用另外一种更加高级的算法来获得最终结果。虽然我们不会在本章使用集成技术，但是大家还是有必要记住这种技术。

　　实际上，在前面的章节中我们已经接触过机器学习算法了，朴素贝叶斯分类算法便是其中之一。我们可以将机器学习分为下列几种类型。

• 监督学习：要求为训练数据提供标签，也就是说需要给算法提供已经分好类的样本。利用带标签的训练数据，我们可以创建一个函数，将输入变量映射为相应的输出变量。比如，如果想对垃圾邮件进行分类，那么我们必须提供垃圾邮件和正常电子邮件的相应样本。监督学习算法的例子包括线性回归、逻辑回归、状态向量机、随机森林、K最近邻算法等。
• 无监督学习：这类机器学习算法不需要人工输入。它能够自行发现数据中存在的模式，如大型数据集中的聚类等。无监督学习算法的例子包括K均值和分层聚类。
• 强化学习：这种类型的学习技术无需进行辅导，但是需要我们提供一些反馈信息。例如一台电脑可以跟它自己下棋，或者玩1983的《战争游戏》电影中的井字游戏和热核战争游戏。

　　下面我们以天气预报为例进行说明。本章会大量用到一个Python程序库，即scikit- learn。虽然这个程序库提供了许多聚类分析算法、回归算法和分类算法，但是，还有一些机器学习算法未包含在scikit-learn中，因此，我们还需要用到其他一些API。本章涉及的主题如下。

• 预处理
• 基于逻辑回归的分类
• 基于支持向量机的分类
• 基于ElasticNetCV的回归分析
• 支持向量回归
• 基于相似性传播（affinity propagation）的聚类分析
• 均值漂移算法
• 遗传算法
• 神经网络
• 决策树算法

 

10.1预处理

 　　在scikit-learn库中提供了一个预处理模块，下面我们将详细介绍该模块。在第9章中，我们已经安装了scikit-learn并且已经做过一次数据预处理了，即过滤掉剔除字（Stopwords）。一些机器学习算法对某些数据比较头疼，因为这些数据不服从高斯分布，即不满足数学期望为0、标准方差为1的条件。模块sklearn.preprocessing从而应运而生，本节将详细介绍这个模块的使用方法，我们会针对来自荷兰皇家气象学会的气象数据进行预处理。比尔特（DE BILT）气象研究中心的原始数据较多，我们所要的数据只是原始数据文件中的一列而已，这一列记录的是日降雨量。需要的数据将使用第5章中介绍的.npy格式来存放。下面把数据加载到一个NumPy数组中。这些整数值必须全部乘以0.1，从而得到以毫米为单位的日降水量。

　　该数据有一个很诡异的地方，那就是凡是小于 0.05mm的数值，都将用作−1。因此，我们把这些数值全部设为0.025，即0.05的一半。在原始数据中，如果某一天的降雨量低于这些数值，那么这一天将不会记录在案。对于这样的缺失数据，我们将完全忽略。我们可以那么做，因为本来缺失的数据点就非常多，所以也不差这一点。例如，本世纪初大约缺失一年的数据，同时后来许多天的数据也是缺失的。在preprocessing模块中，它的Imputer类提供了许多处理缺失数据的默认策略。不过，这些策略对于本节讨论的内容而言，好像不太合适。数据分析如同一扇透视数据的窗口，一扇通向知识的窗口。数据的清洗和填补可以使我们的窗口看起来更加清爽。可是，我们应该注意不要过于扭曲原始数据。

　　这里的机器学习样本的主要特征是一个数组，用来存放表示一年中各天（1～366）日期的数值。这些可以帮助解释季节影响因素。

　　期望值、标准差和安德森-达林（Anderson-Darling）检验结果（详情请参阅第4章）如下

Rain mean 2.17919594267
Rain variance 18.803443919
Anderson rain (inf, array([ 0.576,  0.656,  0.787, 0.918,1.092]), array([ 15. ,  10. ,   5. ,   2.5,   1. ]))

　　透过以上输出内容，可以得出可靠的结论，该数据不满足数学期望为0标准方差为1的要求，因此它不符合正态分布。在这个数据集中，0值占比很大，说明在这些天没有下雨。大的降雨量已经越来越罕见（这倒是一件好事）。数据分布情况完全不对称，因此，这不是一个高斯分布。下面通过scale()函数对数据进行缩放处理，代码如下。

scaled = preprocessing.scale(rain)

　　如今，数学期望和标准方差已经满足要求，只是数据的分布还是不对称。

Scaled mean 3.4130160280768244e-17
Scaled variance 1.0
Anderson scaled AndersonResult(statistic=5731.267850009339, critical_values=array([0.576, 0.656, 0.787, 0.918, 1.092]), 
significance_level=array([15. , 10. ,  5. ,  2.5,  1. ]))

　　有时，我们需要把特征值由数值型转换为布尔型。例如，进行文本分析时就经常需要进行此类变换，以简化计算。这时，可以借助binarize()函数进行类型转换，代码如下。

binarized = preprocessing.binarize(rain.reshape(-1,1))
print(np.unique(binarized), binarized.sum())

　　默认情况下，这将生成一个新数组；此外，我们还让它进行了某些运算。默认的阈值为0。也就是说，正值用1替代，负值用0替代。

[0. 1.] 24594.0

　　进行分类时，类LabelBinarizer可以用整数来标注类别。

lb = preprocessing.LabelBinarizer()
lb.fit(rain.astype(int))
print(lb.classes_)

　　上述代码的输出0～62的一组整数。相关代码摘自本书代码包中的ch-10.ipynb文件。

import numpy as np
from sklearn import preprocessing
from scipy.stats import anderson

rain = np.load('rain.npy')
rain = .1 * rain
rain[rain < 0] = .05/2
print("Rain mean", rain.mean())
print("Rain variance", rain.var())
print("Anderson rain", anderson(rain))

scaled = preprocessing.scale(rain)
print("Scaled mean", scaled.mean())
print("Scaled variance", scaled.var())
print("Anderson scaled", anderson(scaled))

binarized = preprocessing.binarize(rain.reshape(-1,1))
print(np.unique(binarized), binarized.sum())

lb = preprocessing.LabelBinarizer()
lb.fit(rain.astype(int))
print(lb.classes_)

10.2基于逻辑回归的分类

 　　逻辑回归是一种分类算法，这种算法可以用于预测事件发生的概率或者某事物属于某一类别的概率。对于多元分类问题，可以将其简化为二元分类问题。在最简单的情形下，某一类别的概率高，则意味着另一个类别的概率低。逻辑回归是以logistic函数为基础的，该函数的取值介于0～1中间，这与概率值正好吻合。因此，可以利用logistic函数将任意值转换为一个概率。

　　为了使用逻辑回归进行分类，需要定义一个相应的函数。下面开始创建分类器对象，代码如下。

 clf = LogisticRegression(random_state=12)

　　参数random_state的作用，类似为随机数生成器指定的种子。之前已经讲过，交叉验证在避免过拟合方面有着非常重要的作用。K-折交叉验证是一种交叉验证技术，它会把数据集随机分为k（一个小整数）份，每一份称为一个包。在这k次迭代过程中，每个包会有1次被用于验证，其余9次用于训练。对于scikit-learn来说，它每个类的默认k值都是3，但是，通常需要将这个值设置得更大一些，如5或10。迭代的结果可以在最后进行合并。对于k-折交叉验证，scikit-learn专门提供了一个KFold类。为了创建一个具有10个包的KFold对象，可以使用下列代码。

kf = KFold(n_splits=10)

　　然后，使用fit()函数训练数据，代码如下。

clf.fit(x[train], y[train])

　　为了衡量分类的准确性，可以使用score()方法，具体如下。

scores.append(clf.score(x[test], y[test]))

　　在这个例子中，可以把日期和日降雨量作为特征，下面使用这些特征来构造一个数组，代码如下。

x = np.vstack((dates[:-1], rain[:-1]))

　　因为要进行分类，所以首先要定义无降雨天，即降雨量为0；然后用−1表示有微弱降雨的小雨天；最后剩下的就是雨天。我们把这3种类别与数据值的符号关联起来。

y = np.sign(rain[1:])

　　据此，得到的平均准确率为57%。在scikit-learn的数据集上，我们的平均准确率为41%，代码具体参考本书代码包中的log_regress.py文件。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold
from sklearn import datasets
import numpy as np

def classify(x, y):
    clf = LogisticRegression(random_state=12)
    scores = []
    kf = KFold(n_splits=10)
    for train,test in kf.split(x):
      clf.fit(x[train], y[train])
      scores.append(clf.score(x[test], y[test]))

    print("Accuracy: ",np.mean(scores))

rain = np.load('rain.npy')
dates = np.load('doy.npy')

x = np.vstack((dates[:-1], rain[:-1]))
y = np.sign(rain[1:])
classify(x.T, y)

#iris example
iris = datasets.load_iris()
x = iris.data[:, :2]
y = iris.target
classify(x, y)

 

Accuracy:  0.577211706428828
Accuracy:  0.7066666666666667

 

10.3基于支持向量机的分类

　　支持向量机（Support Vector Machines，SVM）不仅可以用来进行回归分析，如支持向量回归（Support Vector Regression，SVR），而且还可以用来进行分类，支持向量机算法是Vladimir Vapnik于1993年发明出来的。

　　SVM可以把数据点映射到多维空间的数据点，这种映射是通过核函数来完成的。这里的核函数既可以是线性的，也可以是非线性的。这样，分类问题就简化为寻找一个将空间一分为二的超平面，或者是能够将数据点恰如其分地划分到不同空间（类别）的多个超平面。利用超平面进行分类是一件非常困难的事情，因为这会引出软间隔的概念。软间隔用来表示对错误分类的容忍度，通常由一个用C表示的常量给出。另一个重要的参数就是核函数的类型，有如下几种。

• 线性函数
• 多项式函数
• 径向基函数
• Sigmoid函数

　　网格搜索法可以用来寻找合适的参数，这是一种系统性的方法，即尝试所有可能的参数组合。为了进行网格搜索，可以借助scikit-learn提供的GridSearchCV类。使用这个类时，我们可以通过字典来提供分类器或回归器的类型对象。字典的键就是我们将要调整的参数，而字典的值就是需要尝试的参数值的相应列表。对于用来进行分类和回归分析的那些类，scikit-learn API都有对应的、为其提供了添加交叉验证功能的类。不过，默认情况下，交叉验证功能都未启用。下面创建一个GridSearchCV对象，代码如下。

    clf = GridSearchCV(SVC(random_state=42, max_iter=100), {'kernel': ['linear', 'poly', 'rbf'], 'C':[1, 10]})

　　上面的代码规定了最多迭代次数，这个数字不要太大，否则对我们的耐心绝对是一个严峻的考验。此外，这里没有启用交叉验证，为的是加速处理过程。而且，我们还指定了核方法的类型以及软间隔的相应参数。

　　上述代码为可能的参数变异创建了一个2×3的网格。如果时间宽裕，我们可以创建一个更大的网格来包含更多的可能值。另外，我们可以把GridSearchCV的cv参数的值设为预期的包总量，如5或10。实际上，最多迭代次数设置得越高越好。至于不同的核方法，可以根据拟合的实际情况择机而用。如果把参数verbose设置为一个非零整数，那就可以得到每个参数值组合更为详尽的输出信息，如执行时间等。通常情况下，我们希望按照幅值大小的顺序，如1～10 000，依次变换 soft-margin 参数的取值，这时可以借助 NumPy 的logspace()函数来完成。

　　使用这个分类器时，在天气数据上得到的准确性是56%，在鸢尾花样本数据集上得到的准确性是82%。GridSearchCV的gridscores区保存有网格搜索的成效数据。对于天气数据，成效数据如下。

Accuracy:  0.4752925545505647
{'mean_fit_time': array([0.10729136, 0.15199084, 0.27729039, 0.07938633, 0.15557127,
       0.26728883]),
 'mean_score_time': array([0.02516398, 0.03653703, 0.07361264, 0.01555986, 0.03631983,
       0.070818  ]),
 'mean_test_score': array([0.42610763, 0.53735336, 0.28585569, 0.29270417, 0.53349511,
       0.28585569]),
 'param_C': masked_array(data=[1, 1, 1, 10, 10, 10],
             mask=[False, False, False, False, False, False],
       fill_value='?',
            dtype=object),
 'param_kernel': masked_array(data=['linear', 'poly', 'rbf', 'linear', 'poly', 'rbf'],
             mask=[False, False, False, False, False, False],
       fill_value='?',
            dtype=object),
 'params': [{'C': 1, 'kernel': 'linear'},
            {'C': 1, 'kernel': 'poly'},
            {'C': 1, 'kernel': 'rbf'},
            {'C': 10, 'kernel': 'linear'},
            {'C': 10, 'kernel': 'poly'},
            {'C': 10, 'kernel': 'rbf'}],
 'rank_test_score': array([3, 1, 5, 4, 2, 5]),
 'split0_test_score': array([0.40252938, 0.55952989, 0.23441492, 0.5167348 , 0.55556975,
       0.23441492]),
 'split1_test_score': array([0.31732243, 0.55838017, 0.38924374, 0.21525294, 0.55620848,
       0.38924374]),
 'split2_test_score': array([0.55799693, 0.55825243, 0.41377108, 0.29036791, 0.55697496,
       0.41377108]),
 'split3_test_score': array([0.55960138, 0.45189728, 0.16877475, 0.30586432, 0.45189728,
       0.16877475]),
 'split4_test_score': array([0.29308803, 0.55870704, 0.22307397, 0.13530088, 0.54682509,
       0.22307397]),
 'std_fit_time': array([0.00754749, 0.00337823, 0.01541952, 0.00506452, 0.00372173,
       0.01022942]),
 'std_score_time': array([0.00146306, 0.00118295, 0.00172066, 0.00135341, 0.00120141,
       0.00209969]),
 'std_test_score': array([0.11428013, 0.04273036, 0.09731092, 0.12739141, 0.04096434,
       0.09731092])}

　　对于鸢尾花样本数据来说，我们的成绩如下。

Accuracy:  0.82
{'mean_fit_time': array([0.0009974 , 0.00099716, 0.00099726, 0.00079803, 0.0009974 ,
       0.00119658]),
 'mean_score_time': array([0.00039902, 0.        , 0.00019932, 0.00039868, 0.00019941,
       0.00019956]),
 'mean_test_score': array([0.80666667, 0.73333333, 0.82      , 0.76666667, 0.59333333,
       0.81333333]),
 'param_C': masked_array(data=[1, 1, 1, 10, 10, 10],
             mask=[False, False, False, False, False, False],
       fill_value='?',
            dtype=object),
 'param_kernel': masked_array(data=['linear', 'poly', 'rbf', 'linear', 'poly', 'rbf'],
             mask=[False, False, False, False, False, False],
       fill_value='?',
            dtype=object),
 'params': [{'C': 1, 'kernel': 'linear'},
            {'C': 1, 'kernel': 'poly'},
            {'C': 1, 'kernel': 'rbf'},
            {'C': 10, 'kernel': 'linear'},
            {'C': 10, 'kernel': 'poly'},
            {'C': 10, 'kernel': 'rbf'}],
 'rank_test_score': array([3, 5, 1, 4, 6, 2]),
 'split0_test_score': array([0.73333333, 0.7       , 0.73333333, 0.73333333, 0.56666667,
       0.73333333]),
 'split1_test_score': array([0.83333333, 0.86666667, 0.86666667, 0.83333333, 0.5       ,
       0.83333333]),
 'split2_test_score': array([0.76666667, 0.66666667, 0.76666667, 0.76666667, 0.6       ,
       0.8       ]),
 'split3_test_score': array([0.86666667, 0.56666667, 0.86666667, 0.86666667, 0.9       ,
       0.83333333]),
 'split4_test_score': array([0.83333333, 0.86666667, 0.86666667, 0.63333333, 0.4       ,
       0.86666667]),
 'std_fit_time': array([3.23406696e-07, 4.67203091e-07, 2.78041453e-07, 3.99017505e-04,
       1.90734863e-07, 3.98779158e-04]),
 'std_score_time': array([0.00048869, 0.        , 0.00039864, 0.00048829, 0.00039883,
       0.00039911]),
 'std_test_score': array([0.04898979, 0.11737878, 0.05811865, 0.08164966, 0.16786238,
       0.04521553])}

　　相关代码取自本书代码包中的ch-10.ipynb文件。

from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
from pprint import PrettyPrinter

def classify(x, y):
    clf = GridSearchCV(SVC(random_state=42, max_iter=100), {'kernel': ['linear', 'poly', 'rbf'], 'C':[1, 10]})
    clf.fit(x, y)
    print("Accuracy: ", clf.score(x, y))
    PrettyPrinter().pprint(clf.cv_results_)

rain = np.load('rain.npy')
dates = np.load('doy.npy')

x = np.vstack((dates[:-1], rain[:-1]))
y = np.sign(rain[1:])

classify(x.T, y)

#iris example
iris = datasets.load_iris()
x = iris.data[:, :2]
y = iris.target
classify(x, y)

10.4基于ElasticNetCV的回归分析

 　　弹性网络正则化（Elastic Net Regularization）是一种降低回归分析的过拟合风险的方法。弹性网络正则化实际上就是LASSO（The Least Absolute Shrinkage and Selection Operator，LASSO）算法和岭回归方法的线性组合。LASSO能够有效约束L1范数或曼哈顿距离。对于两点来说，L1范数表示的是它们坐标值之差的绝对值之和。岭回归方法使用L1范数的平方作为惩罚项。处理回归问题时，拟合优度通常是由所谓的R平方的判定系数来判断的。令人遗憾的是，R平方的定义并不统一。此外，这个名称还有误导之嫌，因为实际上它可以为负数。就拟合优度而言，最好的情况下其判定系数为1。根据判定系数的定义看，其允许的取值范围还是不小的，但是我们的目标很明确，就是设法让它向1靠拢。

下面我们使用10-折交叉验证并定义一个ElasticNetCV对象，代码如下。

    clf = ElasticNetCV(max_iter=200, cv=10, l1_ratio = [.1, .5, .7, .9, .95, .99, 1])

　　这里，ElasticNetCV类使用了一个名为l1_ratio的参数，其取值为0～1。如果该参数的值为0，只使用岭回归算法；如果该参数的值为1，只使用LASSO回归算法；否则，就使用混合算法。对于这个参数，可以给它指定单个数值，也可以给它提供一个数值列表。对于降雨数据，我们得分情况如下。

Score 0.052783876094198205

　　这个得分表明，我们对数据训练不足，或者说产生欠拟合（underftting）。出现这种情况的原因有很多，如特征数量不足或者选用的模型不合适等。对于波士顿房价数据，针对现有的特征得分如下。

Score 0.6831524128217573

　　Predict()方法可以针对新数据进行预测。对于预测的结果，我们可以使用散点图来可视化其效果。对于降雨数据，得到的散点图如图10-1所示。

 

 

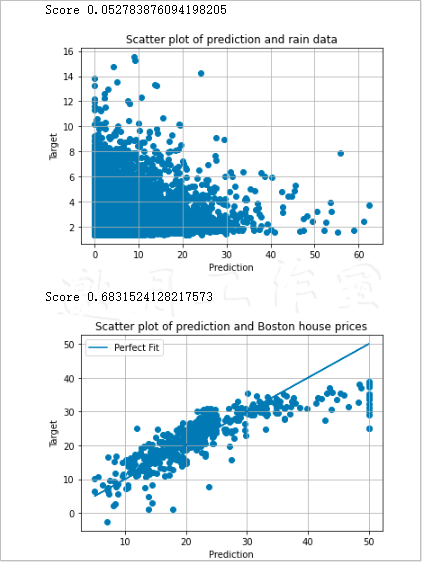
　　观察图10-1可以发现，这次的拟合效果不佳，即欠拟合。穿过原点的对角线，才是最理想的拟合曲线，就像图10-2所示的波士顿房价数据拟合情况。如上，两图合并

 

相关代码摘自本书代码包中的ch-10.ipynb文件。

from sklearn.linear_model import ElasticNetCV
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt

def regress(x, y, title):
    clf = ElasticNetCV(max_iter=200, cv=10, l1_ratio = [.1, .5, 
.7, .9, .95, .99, 1])

    clf.fit(x, y)
    print("Score", clf.score(x, y))

    pred = clf.predict(x)
    plt.title("Scatter plot of prediction and " + title)
    plt.xlabel("Prediction")
    plt.ylabel("Target")
    plt.scatter(y, pred)
    # Show perfect fit line
    if "Boston" in title:
        plt.plot(y, y, label="Perfect Fit")
        plt.legend()

    plt.grid(True)
    plt.show()

rain = .1 * np.load('rain.npy')
rain[rain < 0] = .05/2
dates = np.load('doy.npy')

x = np.vstack((dates[:-1], rain[:-1]))
y = rain[1:]
regress(x.T, y, "rain data")

boston = datasets.load_boston()
x = boston.data
y = boston.target
regress(x, y, "Boston house prices")

 

10.5支持向量回归

 　　如前所述，支持向量机也可以用于回归分析。就回归来说，我们是通过超平面而非单独的点来拟合数据的。学习曲线是一种将学习算法行为特点可视化的好办法。对于不同的训练数据量来说，学习曲线都是训练成效和测试成效所考量的一部分。创建学习曲线可能迫使我们重复训练估计器，因此会导致整体过程变慢。对此，我们可以通过使用多个并行估计器作业进行补偿。

　　支持向量回归是需要进行标定处理（scaling）的算法之一。

　　我们得到的两个高分如下。

Max test score Rain 0.0161004084576
Max test score Boston 0.662188537037

　　这与ElasticNetCV类得到的结果相仿。为此，许多scikit-learn类都提供了一个n_jobs参数。根据经验，通常系统中有几个CPU，我们就创建几个作业。创建作业时，可以借助Python标准的多进程API。为了进行训练和测试，可以调用learning_curve()函数，代码　 如下。

train_sizes, train_scores, test_scores = learning_curve(clf, X, Y, n_jobs=ncpus) 

　　求平均数，然后画出相应的得分情况。

    plt.plot(train_sizes, train_scores.mean(axis=1), label="Train score")
    plt.plot(train_sizes, test_scores.mean(axis=1), '--', label="Test score")

　　降雨数据的学习曲线大致如图10-3所示。

 

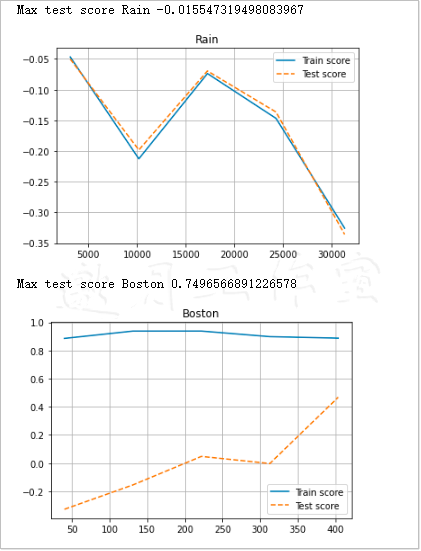
　　学习曲线在日常生活中也较常见，即练习的次数越多，学到的就越多。按照数据分析术语来讲，数据越多，学习的效果越好。如果训练成绩不错，但是测试效果不好，这就说明出现了过拟合现象。也就是说，我们的模型只适用于训练数据。图10-4所示是波士顿房价数据的学习曲线，它看起来更好一些。两图已合并。

　　代码取自本书代码包中的sv_regress.py文件。

import numpy as np
from sklearn import datasets
from sklearn.model_selection import learning_curve
from sklearn.svm import SVR
from sklearn import preprocessing
import multiprocessing
import matplotlib.pyplot as plt

def regress(x, y, ncpus, title):
    X = preprocessing.scale(x)
    Y = preprocessing.scale(y)
    clf = SVR(max_iter=ncpus * 200)

    train_sizes, train_scores, test_scores = learning_curve(clf, X, Y, n_jobs=ncpus) 

    plt.figure()
    plt.title(title)
    plt.plot(train_sizes, train_scores.mean(axis=1), label="Train score")
    plt.plot(train_sizes, test_scores.mean(axis=1), '--', label="Test score")
    print("Max test score " + title, test_scores.max())
    plt.grid(True)
    plt.legend(loc='best')
    plt.show()

rain = .1 * np.load('rain.npy')
rain[rain < 0] = .05/2
dates = np.load('doy.npy')

x = np.vstack((dates[:-1], rain[:-1]))
y = rain[1:]
ncpus = multiprocessing.cpu_count()
regress(x.T, y, ncpus, "Rain")

boston = datasets.load_boston()
x = boston.data
y = boston.target
regress(x, y, ncpus, "Boston")

 

10.6基于相似性传播算法的聚类分析

　　聚类分析，就是把数据分成一些组，这些组即所谓的聚类。聚类分析通常无需提供目标数据，从这个意义上来说，它属于无监督学习方法。一些聚类算法需要对聚类数进行推测，而另一些聚类算法则不必如此，相似性传播（Affinity Propagation，AP）算法就属于后一类算法。数据集中的各个元素都会通过特征值被映射到欧氏空间，然后计算数据点之间的欧氏距离，以此构建一个矩阵，这个矩阵就是AP算法的基础。因为这个矩阵可能会迅速膨胀，对此我们一定要当心，不要让它耗尽内存。实际上，scikit-learn程序库提供了一个实用程序，来帮我们生成结构化数据。下面我们通过代码生成3个数据块，具体如下。

x, _ = datasets.make_blobs(n_samples=100, centers=3, n_features=2, 
random_state=10)

　　调用euclidean_distances()函数，创建前面提到的矩阵。

S = euclidean_distances(x)

　　利用这个矩阵，我们就可以给数据标注其所属的聚类了，代码如下。

aff_pro = cluster.AffinityPropagation().fit(S)
labels = aff_pro.labels_

　　绘制聚类后，得到的图像如图10-5所示。

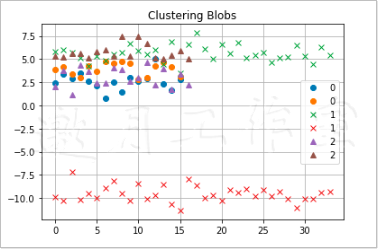
　　以上代码摘自本书代码包中的ch-10.ipynb.py文件。

from sklearn import datasets
from sklearn import cluster
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import euclidean_distances

x, _ = datasets.make_blobs(n_samples=100, centers=3, n_features=2, 
random_state=10)
S = euclidean_distances(x)

aff_pro = cluster.AffinityPropagation().fit(S)
labels = aff_pro.labels_

styles = ['o', 'x', '^']

for style, label in zip(styles, np.unique(labels)):
   print(label)
   plt.plot(x[labels == label], style, label=label)
plt.title("Clustering Blobs")
plt.grid(True)
plt.legend(loc='best')
plt.show()

 

10.7均值漂移算法

 　　均值漂移算法是另外一种不需要估算聚类数的聚类算法。目前，这个算法已经成功应用于图像处理。该算法通过迭代来寻找一个密度函数的最大值。展示均值漂移算法前，我们首先需要使用pandas DataFrame计算日降雨量的平均值。下面来创建DataFrame并计算其数据的平均值，代码如下。

df = pd.DataFrame.from_records(x.T, columns=['dates', 'rain'])
df = df.groupby('dates').mean()
df.plot()

　　结果如图10-6所示。

 

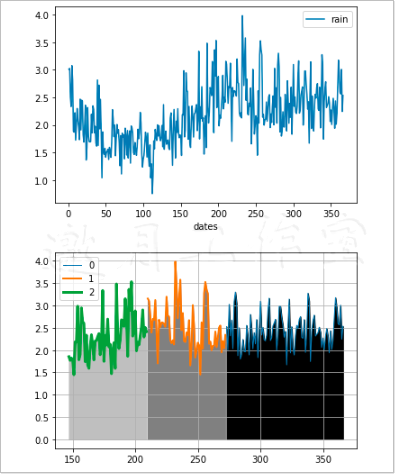
基于均值漂移算法的聚类代码如下所示。

x = np.vstack((np.arange(1, len(df) + 1) , df.values.ravel()))
x = x.T
ms = cluster.MeanShift()
ms.fit(x)

如果使用不同的线宽和阴影，那么绘制出的3个聚类如图10-7所示。

两图合并如上。

如你所见，我们根据年内日平均雨量（以mm为单位）划分出3个聚类。完整的代码摘自本书代码包中的ch-10.ipynb文件。

import numpy as np
from sklearn import cluster
import matplotlib.pyplot as plt
import pandas as pd

rain = .1 * np.load('rain.npy')
rain[rain < 0] = .05/2
dates = np.load('doy.npy')
x = np.vstack((dates, rain))
df = pd.DataFrame.from_records(x.T, columns=['dates', 'rain'])
df = df.groupby('dates').mean()
df.plot()
# x = np.vstack((np.arange(1, len(df) + 1) ,  df.as_matrix().ravel()))
#'DataFrame' object has no attribute 'as_matrix'，改为df.values即可，邀月注
x = np.vstack((np.arange(1, len(df) + 1) , df.values.ravel()))
x = x.T
ms = cluster.MeanShift()
ms.fit(x)
labels = ms.predict(x)

plt.figure()
grays = ['0', '0.5', '0.75']

for gray, label in zip(grays, np.unique(labels)):
    match = labels == label
    x0 = x[:, 0]
    x1 = x[:, 1]
    plt.plot(x0[match], x1[match], lw=label+1, label=label)
    plt.fill_between(x0, x1, where=match, color=gray)

plt.grid(True)
plt.legend()
plt.show()

 

10.8遗传算法

 　　遗传算法是本书最具争议的部分，这种算法基于生物学领域的进化论。这种类型的算法在搜索和优化方面用途广泛，例如，可以使用遗传算法来搜索回归问题或分类问题的最佳参数。

　　在地球上，人类及其他生命形式都通过染色体来携带遗传信息。通常，我们使用字符串对染色体进行建模。在遗传算法中，我们也沿用了这种类似的遗传信息表示方法。算法的第一步是，利用随机个体初始化种群并使用相应的表示方法表达遗传信息。此外，我们还可以使用待解决问题的已知候选解来进行初始化。之后，我们需要进入一个迭代处理过程，即所谓的逐代（generation）演化。对于每一代个体，算法都会根据预定义的适应度函数来选择一些个体，作为交配个体供下一步杂交用。适应度函数的作用是评估个体与满意解的接近程度。

　　下面介绍两种遗传算子（genetic operators），它们可以用来生成新的遗传信息。

• 交叉（Crossover）：这个遗传操作就是通过交配的方式来产生新个体。这里将介绍单点交叉（one-point crossover）操作，具体操作是，亲本的遗传信息相互交换，从而产生两个新的个体，第1个个体前半段遗传信息取自父本，后半段取自母本，第2个个体正好相反。例如，假设遗传信息使用100个列表元素来表示，那么交叉操作可以从亲本中的一方摘取前80个元素，然后从另一方取得后20个元素。当然，对于遗传算法来说，它能够通过交叉两个以上的父本和母本来繁殖新个体，这一技术正处于研究阶段（详情参见Eiben, A. E. et al. Genetic algorithms with multi-parent recombination, Proceedings of the International Conference on Evolutionary Computation- PPSN III. The Third Conference on Parallel Problem Solving from Nature: 78-87. ISBN 3-540-58484-6, 1994）。
• 突变（Mutation）：这个遗传算子受固定突变率的限制。这个概念在好莱坞电影和大众文化中屡见不鲜。我们知道，突变虽然极为罕见，但是却能带来致命危害。不过，有时候突变也能带来我们梦寐以求的特性，而且在某些情况下，这些特性还能够遗传到下一代。

　　最终，新个体会取代旧个体，这时，我们就可以进入下一轮迭代了。本例中，我们将使用Python的DEAP程序库来演示遗传算法。我们安装DEAP，具体方法如下。

$ pip3 install deap

　　首先，定义最大化适应度的Fitness子类，具体如下。

creator.create("FitnessMax", base.Fitness, weights=(1.0,))

　　然后，为种群中的个体定义一个模板。

creator.create("Individual", array.array, typecode='d', 
fitness=creator.FitnessMax)

　　DEAP中的工具箱用来注册必需的函数。下面创建一个工具箱并注册初始化函数，代码如下。

toolbox = base.Toolbox()
toolbox.register("attr_float", random.random)
toolbox.register("individual", tools.initRepeat, 
creator.Individual, toolbox.attr_float, 200)
toolbox.register("populate", tools.initRepeat, list, 
toolbox.individual)

　　第1个函数的作用是产生浮点数，这些数的取值范围为0～1。第2个函数的作用是生成一个个体，它实际上是一个由200个浮点数组成的列表。第3个函数的作用是创建由个体构成的列表，这个列表代表的是一个种群，也就是搜索或优化问题的一组可能解。

　　现实社会中，大部分人都很“普通”，或者说很“正常”，但是也有极少数人很“另类”，如爱因斯坦。第3章曾经介绍了一个shapiro()函数，它可以用来进行正态检验。对于一个个体是否为普通个体，我们需要通过其正态检验p值来衡量它是普通个体的可能性有多大。下面的代码将定义一个适应度函数。

def eval(individual):
    return shapiro(individual)[1],

　　下面定义遗传算子，代码如下。

toolbox.register("evaluate", eval)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutFlipBit, indpb=0.1)
toolbox.register("select", tools.selTournament, tournsize=4)

　　下面对这些遗传算子进行简单解释。

• Evaluate：即评估算子。这项操作用来度量各个个体的适应度。本例中，正态检验的p值便是适应度的衡量指标。
• Mate：即交配算子。这项操作用来产生子代。本例中采用的是两点交叉。
• Mutate：即突变算子。这项操作会随机修改个体。对于由布尔值构成的列表而言，这就意味着某些值会被反转，即由True变为False，或者正好相反。
• Mutate：即选择算子。这项操作用来选择可以进行交配的个体。

　　在上面的代码中，我们规定使用两点交叉，同时指定了属性被翻转的概率，下面生成一个由400个个体组成的原始群体，代码如下。

pop = toolbox.populate(n=400)

　　现在，启动进化过程，代码如下。

hof = tools.HallOfFame(1)
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register("max", np.max)

algorithms.eaSimple(pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=80, 
stats=stats, halloffame=hof)

　　这个程序将提供包括每代最大适应度在内的各种统计信息。我们给它规定了交叉概率、突变率和最大代数（maximum generations），即超过这个代数后就会停止运行。下面的数据就是摘自这个程序输出的统计报告。

gen    nevals    max        
0      400       0.000484774
1      222       0.000656187
2      246       0.00745961 
3      239       0.00745961 
4      240       0.0184182  
5      216       0.0309736  
6      237       0.06957    
7      243       0.06957    
8      231       0.224381   
9      226       0.224381   
10     247       0.224381   
11     228       0.247313   
12     241       0.28318    
13     242       0.354144   
14     246       0.46282    
15     239       0.46282    
16     266       0.480937   
17     233       0.648529   
18     266       0.703452   
19     229       0.742139   
20     249       0.791523   
21     227       0.795744   
22     241       0.856505   
23     237       0.898701   
24     242       0.949595   
25     237       0.949595   
26     249       0.950638   
27     245       0.961397   
28     226       0.974227   
29     235       0.974227   
30     239       0.99192    
31     225       0.99192    
32     252       0.99192    
33     255       0.992183   
34     234       0.995053   
35     250       0.995053   
36     228       0.995053   
37     252       0.995466   
38     228       0.996523   
39     265       0.996992   
40     221       0.99771    
41     238       0.998339   
42     248       0.997815   
43     226       0.998156   
44     236       0.998442   
45     257       0.998442   
46     247       0.998485   
47     227       0.998564   
48     243       0.998564   
49     242       0.998692   
50     237       0.998692   
51     233       0.998692   
52     240       0.998692   
53     252       0.998692   
54     245       0.998713   
55     245       0.998713   
56     239       0.998713   
57     220       0.998713   
58     239       0.998782   
59     247       0.998838   
60     238       0.998838   
61     235       0.998838   
62     248       0.998861   
63     236       0.998861   
64     240       0.998861   
65     210       0.998861   
66     240       0.998861   
67     217       0.998861   
68     239       0.998861   
69     255       0.998861   
70     228       0.998861   
71     254       0.998861   
72     211       0.998861   
73     252       0.998861   
74     250       0.998861   
75     231       0.998861   
76     230       0.998861   
77     252       0.998861   
78     232       0.998861   
79     243       0.998861   
80     235       0.998861   
0.9988605380058289

　　可见，最初的分布与正态分布相去甚远，但是，最终得到的个体的分布情况如图10-8所示。

 

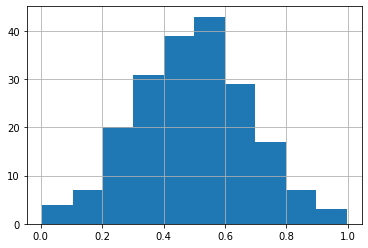
相关代码摘自本书代码包中的ch-10.ipynb文件：

import array
import random
import numpy as np
from deap import algorithms
from deap import base
from deap import creator
from deap import tools
from scipy.stats import shapiro
import matplotlib.pyplot as plt

creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", array.array, typecode='d', 
fitness=creator.FitnessMax)

toolbox = base.Toolbox()
toolbox.register("attr_float", random.random)
toolbox.register("individual", tools.initRepeat, 
creator.Individual, toolbox.attr_float, 200)
toolbox.register("populate", tools.initRepeat, list, 
toolbox.individual)

def eval(individual):
    return shapiro(individual)[1],

toolbox.register("evaluate", eval)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutFlipBit, indpb=0.1)
toolbox.register("select", tools.selTournament, tournsize=4)

random.seed(42)

pop = toolbox.populate(n=400)
hof = tools.HallOfFame(1)
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register("max", np.max)

algorithms.eaSimple(pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=80, 
stats=stats, halloffame=hof)

print(shapiro(hof[0])[1])
plt.hist(hof[0])
plt.grid(True)
plt.show()

 

10.9神经网络

 　　人工神经网络（ANN）的计算模型灵感来自高等动物的大脑。所谓神经网络，实际上就是由神经元组成的网络，这些神经元都具有输入和输出。例如，可以将图片像素相关的数值作为神经网络的输入，然后将神经元的输出传递给下一个神经元，依此类推，最终得到一个多层网络。神经网络蕴涵了许多自适应元素，这使得它非常适合用于处理非线性模型和模式识别问题。接下来，我们将再次根据前些年对应某日降雨量和前一日降雨量来预测是否会下雨。因为后面要用到Python库theanets，所以这里先行安装，命令如下。

$ pip3 install theanets nose_parameterized

　　一位技术评审在安装过程中曾经遇到问题，不过更新NumPy和SciPy后，问题就迎刃而解了。首先创建一个Experiment，也就是创建了一个神经网络，然后再对这个网络进行训练。下面的代码将新建一个具有两个输入神经元和一个输出神经元的神经网络。

net = theanets.Regressor(layers=[2,3,1])

　　该网络拥有一个隐藏层，层内含有3个神经元；另外，这个网络还使用了Python标准的多进程API来加速运算。训练网络所需的数据包括训练样本和验证样本。

train = [x[:N], y[:N]]
valid = [x[N:], y[N:]]

net.train(train,valid,learning_rate=0.1,momentum=0.5)

　　如果要对验证数据进行预测，可以使用以下代码。

pred = net.predict(x[N:]).ravel()

　　Scikit-learn程序库提供了一个实用函数，可以用来计算分类器的准确性。下面是计算准确性的具体代码。

print("Pred Min", pred.min(), "Max", pred.max())
print("Y Min", y.min(), "Max", y.max())
print("Accuracy", accuracy_score(y[N:], pred >= .5))

　　注意，输出值可能每次都不一样，这是神经网络的特性所导致的。这里的输出情况如下。

Pred Min 0.615606596762 Max 0.615606596762
Y Min 0.0 Max 1.0
Accuracy 0.634133878385

　　相关代码摘自本书代码包中的ch-10.ipynb文件。

import numpy as np
import theanets
import multiprocessing
from sklearn import datasets
from sklearn.metrics import accuracy_score

rain = .1 * np.load('rain.npy')
rain[rain < 0] = .05/2
dates = np.load('doy.npy')
x = np.vstack((dates[:-1], np.sign(rain[:-1])))
x = x.T

y = np.vstack(np.sign(rain[1:]),)
N = int(.9 * len(x))

train = [x[:N], y[:N]]
valid = [x[N:], y[N:]]

net = theanets.Regressor(layers=[2,3,1])

net.train(train,valid,learning_rate=0.1,momentum=0.5)

pred = net.predict(x[N:]).ravel()
print("Pred Min", pred.min(), "Max", pred.max())
print("Y Min", y.min(), "Max", y.max())
print("Accuracy", accuracy_score(y[N:], pred >= .5))

　　所有相关的类都报这个错，涉及到引用climate，看来这个包有问题。有知道的朋友请告知邀月，谢谢！

d:\tools\python37\lib\site-packages\theanets\layers\base.py in <module>
     14 from .. import util
     15 
---> 16 logging = climate.get_logger(__name__)
     17 
     18 __all__ = [

AttributeError: module 'climate' has no attribute 'get_logger'

 

10.10决策树

 　　形如if a: else b这样的判断语句，恐怕是Python程序中最常见的语句了。通过嵌套和组合这些语句，就能够建立所谓的决策树。决策树跟老式流程图非常类似，只不过流程图允许循环而已。机器学习领域中，应用决策树的过程通常被称为决策树学习。进行决策树学习时，决策树的末端节点通常又叫作叶节点，其中存放着分类问题的类标签。每个非叶节点都对应特征值之间的一个布尔条件判断。Scikit-learn使用基尼不纯度（Gini impurity）和熵作为信息的衡量指标。实际上，这两种指标衡量的是数据项被错误分类的概率。决策树非常易于理解、使用、可观化和验证。为了形象展示决策树，可以借助 Graphviz，该软件可以从Graphviz官网下载。此外，我们还需要安装pydot2，命令如下。

$ pip3 install pydot2
$ pip3 install pydotplus #这一行必须执行，邀月注

　　　下面把降雨数据分为训练集和测试集两部分，这需要用到scikit-learn提供的traintest split()函数，代码如下。

x_train, x_test, y_train, y_test = train_test_split(x, y, 
random_state=37)

　　创建DecisionTreeClassifier，代码如下。

clf = tree.DecisionTreeClassifier(random_state=37)

　　我们可以使用scikit-learn的RandomSearchCV类来试验各种参数的取值范围，代码如下。

params = {"max_depth": [2, None],
              "min_samples_leaf": sp_randint(1, 5),
              "criterion": ["gini", "entropy"]}
rscv = RandomizedSearchCV(clf, params)
rscv.fit(x_train,y_train)

　　经过一番搜索后，得到的最佳成效和参数如下。

    Best Train Score 0.703164923517
    Test Score 0.705058763413
    Best params {‘criterion’: ‘gini’, ‘max_depth’: 2, ‘min_samples_leaf’:2}

　　在任何情况下，即使只是想验证我们的设想，都不妨将决策树可观化，为此，可以使用下以下代码来绘制决策树的图像。

sio = io.StringIO()
tree.export_graphviz(rscv.best_estimator_, out_file=sio, 
feature_names=['day-of-year','yest'])
dec_tree = pydot.graph_from_dot_data(sio.getvalue())

print("Best Train Score", rscv.best_score_)
print("Test Score", rscv.score(x_test, y_test))
print("Best params", rscv.best_params_)

　　最终结果如图10-9所示。

 

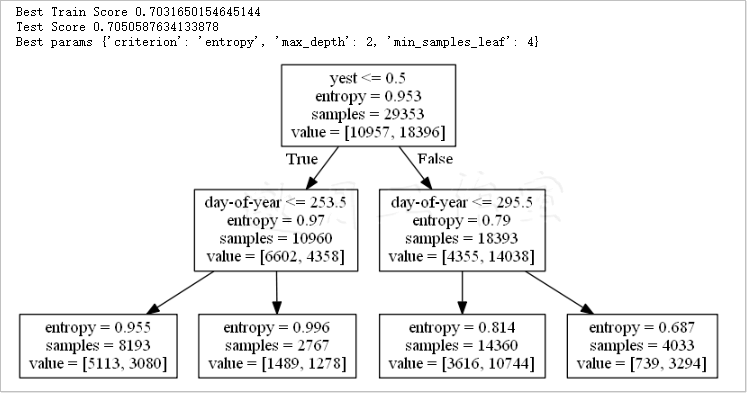
在上面的非叶节点中，各种判断条件都被放置在最上一行，如果条件成立，就进入左侧的子节点；否则，就进入右侧的子节点。当进入一个叶节点时，节点内最下面一行中具有最大值的类别获胜。也就是说，决策树预测输入样本属于该类别。

from sklearn.model_selection import train_test_split
from sklearn import tree
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint as sp_randint
import pydotplus as pydot
import io
import numpy as np
# from tempfile import NamedTemporaryFile

rain = .1 * np.load('rain.npy')
rain[rain < 0] = .05/2
dates = np.load('doy.npy').astype(int)
x = np.vstack((dates[:-1], np.sign(rain[:-1])))
x = x.T

y = np.sign(rain[1:])

x_train, x_test, y_train, y_test = train_test_split(x, y, 
random_state=37)

clf = tree.DecisionTreeClassifier(random_state=37)
params = {"max_depth": [2, None],
              "min_samples_leaf": sp_randint(1, 5),
              "criterion": ["gini", "entropy"]}
rscv = RandomizedSearchCV(clf, params)
rscv.fit(x_train,y_train)

sio = io.StringIO()
tree.export_graphviz(rscv.best_estimator_, out_file=sio, 
feature_names=['day-of-year','yest'])
dec_tree = pydot.graph_from_dot_data(sio.getvalue())

print("Best Train Score", rscv.best_score_)
print("Test Score", rscv.score(x_test, y_test))
print("Best params", rscv.best_params_)

# print(help(dec_tree.create_png))

#以下解决路径问题，邀月注：InvocationException: GraphViz’s executables not found
import os
os.environ["PATH"] += os.pathsep + 'D:/tools/Graphviz/bin/'  #注意修改你的路径

# from IPython.display import Image
display(Image(dec_tree.create_png()))

 

 10.11小结

 　　本章致力于介绍预测建模和机器学习。对于本章涉及的这些主题，读者如果有兴趣，可以进一步参考Packt出版的相关图书。预测性分析通常利用多种技术（其中包括机器学习），才能做出有效的预测，如判断明天是否有雨等。

　　SVM能够将数据映射到多维空间，因此，我们通过它可以把分类问题简化为寻找最佳的一个或多个超平面来区隔数据点，从而达到分类目的。

　　弹性网络正则化则是LASSO方法和岭回归方法的线性组合。处理回归问题时，拟合优度通常是通过判定系数，即所谓的R平方来确定的。一些聚类算法需要推测聚类数，而另一些则没有这样的要求。

　　对于遗传算法，我们要做的第一步是根据随机个体和遗传信息的表示方法来初始化种群。对于每一代个体，都会根据预定义的适应度函数选出一些个体用于配种。机器学习领域中，运用决策树通常叫作决策树学习。

　　第11章将向大家介绍互用性和云计算。

 

第10章完。

python数据分析个人学习读书笔记-目录索引

 

随书源码官方下载：
https://www.ptpress.com.cn/shopping/buy?bookId=bae24ecb-a1a1-41c7-be7c-d913b163c111

需要登录后免费下载。