《python数据分析（第2版）-阿曼多.凡丹戈》读书笔记第7章-信号处理与时间序列

python数据分析个人学习读书笔记-目录索引

第7章信号处理与时间序列

 　　信号处理是工程和应用数学领域的一个分支，主要用于分析模拟信号和数字信号随时间变化的变量。时间序列分析是信号处理技术的一个分支。时间序列是一个从首次测量开始的数据点的有序列表，数据采样的时间间隔通常是等间距的，如以日或年为间隔进行采样。进行时间序列分析时，数据值的顺序很重要，通常需要设法找出某个值与该序列中之前特定周期数上的另一个数据点或者一组数据点之间的关系。

　　本章以年度日斑周期数据为例介绍时间序列，这些数据可以从一个开源Python项目statsmodels程序包中获得。这些例子要用到NumPy/SciPy、Pandas和statsmodels库。

　　本章涉及以下主题。

• Statsmodels模块
• 移动平均值
• 窗口函数
• 定义协整
• 自相关
• 自回归模型
• ARMA模型
• 生成周期信号
• 傅里叶分析
• 谱分析
• 过滤

7.1Statsmodels模块

 　　如果需安装statsmodels模块，请执行以下命令。

$ pip3 install statsmodels

　　我们打开代码包内的ch-07.ipynb文件，然后修改代码，令其显示statsmodels的子库后，能看到如下输出。

import pkgutil as pu
import numpy as np
import matplotlib as mpl
import scipy as sp
import pandas as pd
import pydoc
import statsmodels as sm
from matplotlib.pylab import rcParams
rcParams['figure.figsize']=15,6

print("Statsmodels version", sm.__version__)

def clean(astr):
   s = astr
   # remove multiple spaces
   s = ' '.join(s.split())
   s = s.replace('=','')

   return s

def print_desc(prefix, pkg_path):
   for pkg in pu.iter_modules(path=pkg_path):
      name = prefix + "." + pkg[1]

      if pkg[2] == True:
         try:
            docstr = pydoc.plain(pydoc.render_doc(name))
            docstr = clean(docstr)
            start = docstr.find("DESCRIPTION")
            docstr = docstr[start: start + 140]
            print(name, docstr)
         except:
            continue

print("\n")
print_desc("statsmodels", sm.__path__)

　　输出：

Statsmodels version 0.10.2


statsmodels.base 
statsmodels.datasets 
statsmodels.discrete 
statsmodels.distributions 
statsmodels.duration 
statsmodels.emplike 
statsmodels.formula 
statsmodels.gam 
statsmodels.genmod 
statsmodels.graphics 
statsmodels.imputation 
statsmodels.interface 
statsmodels.iolib 
statsmodels.miscmodels 
statsmodels.multivariate 
statsmodels.nonparametric DESCRIPTION For an overview of this module, see docs/source/nonparametric.rst PACKAGE CONTENTS _kernel_base _smoothers_lowess api bandwidths
statsmodels.regression 
statsmodels.resampling 
statsmodels.robust 
statsmodels.sandbox 
statsmodels.src 
statsmodels.stats 
statsmodels.tests 
statsmodels.tools 
statsmodels.tsa 

 

7.2移动平均值

 　　研究时间序列时，我们经常会用到移动平均值。移动平均法需要规定一个窗口，它限定了每一眼能看到数据的数量，窗口每前移一个周期，其中的数据都要计算一次均值。

 　　不同类型的移动平均法主要区别在于求平均值时所用的权重，例如指数移动平均法，权重随时间的变化以指数的形式递减。

 　　这意味着，数据值的位置越靠前，其对均值的影响力愈弱，有时这种特性正是我们所希望的。

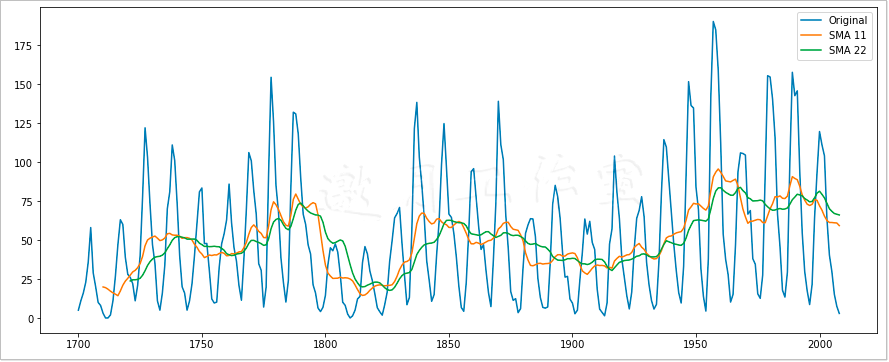
　　以下代码摘自本书代码包中的ch-07.ipynb文件，它将绘制以11年和22年为窗口的太阳黑子周期的简单移动平均值。

import matplotlib.pyplot as plt
import statsmodels.api as sm
# from pandas.stats.moments import rolling_mean

data_loader = sm.datasets.sunspots.load_pandas()
df = data_loader.data
year_range = df["YEAR"].values
plt.plot(year_range, df["SUNACTIVITY"].values, label="Original")
plt.plot(year_range, df.rolling(window=11).mean()["SUNACTIVITY"].values, label="SMA 11")
plt.plot(year_range, df.rolling(window=22).mean()["SUNACTIVITY"].values, label="SMA 22")
plt.legend()
plt.show()

　　指数移动平均的指数式递减加权策略，可以通过下列NumPy代码实现。

weights = np.exp(np.linspace(-1., 0., N))
weights /= weights.sum()

　　简单移动平均值使用的是等量加权策略，相应代码如下。

def sma(arr, n):
   weights = np.ones(n) / n
   return np.convolve(weights, arr)[n-1:-n+1]

　　因为我们可以把数据载入到pandas的DataFrame中，所以这样其rolling_mean()函数使用起来会更加方便。下面我们使用statsmodels库加载数据，代码如下。

data_loader = sm.datasets.sunspots.load_pandas()
df = data_loader.data

　　最终结果如图7-1所示。

 

7.3窗口函数

 　　NumPy提供了许多窗口例程，当像前面所说的那样滚动窗口时，可以用它们计算权重。

　　窗口函数是定义在一个区间（窗口）上的函数，超出定义域，函数值取零。我们可以使用它们来分析频谱、设计滤波器等。Boxcar窗口是一种矩形窗口，公式如下。

W(n) = 1

　　三角形窗口的形状像一个三角形，其公式如下。

 

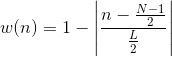
　　上面的公式中，L可以是N、N+1或者N−1。最后介绍的窗口函数是钟形的布莱克曼窗口（Bartlett window），定义如下

 

　　其中,

 

　　汉宁窗（Hanning window）是另外一种钟形窗口函数，定义如下：

 

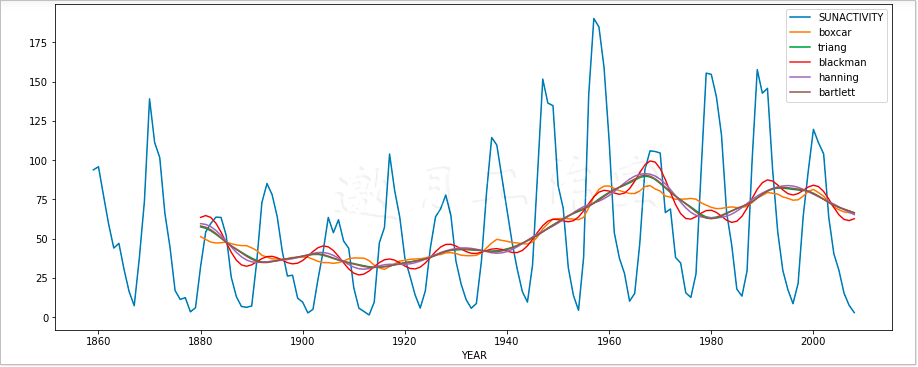
　　根据Pandas的应用程序接口的规定，rolling_window()函数的win_type参数用来规定窗口函数的类型，另一个参数规定窗口的大小，通常设为22，这是太阳黑子数据的中等周期（据研究，存在3个周期，分别为11年、22年和100年）。下面的代码摘自本书代码包中的ch-07.ipynb文件，为了便于在图中进行比较，这里只取近150年的数据。

import matplotlib.pyplot as plt
import statsmodels.api as sm
#from pandas.stats.moments import rolling_window
import pandas as pd

data_loader = sm.datasets.sunspots.load_pandas()
df = data_loader.data.tail(150)
df = pd.DataFrame({'SUNACTIVITY':df['SUNACTIVITY'].values}, index=df['YEAR'])
ax = df.plot()

def plot_window(wintype):
    df2 = df.rolling(window=22,win_type=wintype,center=False,axis=0).mean()
    df2.columns = [wintype]
    df2.plot(ax=ax)

plot_window('boxcar')
plot_window('triang')
plot_window('blackman')
plot_window('hanning')
plot_window('bartlett')
plt.show()

　　最终结果如图7-2所示。

 

7.4协整的定义

 　协整概念类似于关联概念，但是许多人认为，定义两个时间序列相关性时，协整是一种性能优越的衡量指标。如果两个时间序列x(t)和y(t)的线性组合是稳态的，那么就称这两个序列具有共整合性或协整性。在这种情况下，下面的方程式应该是稳态的。

　Y(t) – a x(t)

　　考虑醉汉与狗在一起散步的情形，相关性反映出他们是否在同一个方向上前进。协整性反映的则是一段时间后人和狗之间的距离。下面利用随机生成的时间序列和真实数据来展示协整关系。增广迪基-福勒检验法（Augmented Dickey-Fuller test，ADF）可以测试时间序列中的单位根，也可用于确定时间序列的协整关系。

　　下面的代码摘自本书代码包中的ch-07.ipynb文件。

import statsmodels.api as sm
# from pandas.stats.moments import rolling_window
import pandas as pd
import statsmodels.tsa.stattools as ts
import numpy as np

def calc_adf(x, y):
    result = sm.OLS(x, y).fit()    
    return ts.adfuller(result.resid)

data_loader = sm.datasets.sunspots.load_pandas()
data = data_loader.data.values
N = len(data)

t = np.linspace(-2 * np.pi, 2 * np.pi, N)
sine = np.sin(np.sin(t))
print("Self ADF", calc_adf(sine, sine))

noise = np.random.normal(0, .01, N)
print("ADF sine with noise", calc_adf(sine, sine + noise))

cosine = 100 * np.cos(t) + 10
print("ADF sine vs cosine with noise", calc_adf(sine, cosine + noise))

print("Sine vs sunspots", calc_adf(sine, data))

　　下面开始展示协整性。

　　（1）定义用来计算ADF统计量的函数。

def calc_adf(x, y):
    result = sm.OLS(x, y).fit()    
    return ts.adfuller(result.resid)

　　（2）太阳黑子数据载入NumPy数组。

data_loader = sm.datasets.sunspots.load_pandas()
data = data_loader.data.values
N = len(data)

　　（3）计算正弦值并求出该值与其自身的协整关系。

t = np.linspace(-2 * np.pi, 2 * np.pi, N)
sine = np.sin(np.sin(t))
print("Self ADF", calc_adf(sine, sine))

　　（4）以上代码将打印如下内容。

Self ADF (5.098349840844293e-16, 0.958532086060056, 0, 308,
 {'1%': -3.45176116018037, '5%': -2.870970093607691, '10%': -2.571794416006072}, -21598.896016765088)

　　输出的第1个值是对ADF的度量，第2个值是p值，这里的p值是很高的。接下来是时间延迟和样本量，最后是一个词典，给出了这个样本量的t分布值。

　　（5）下面给正弦波信号添加噪音，看它们是如何影响该信号的。

noise = np.random.normal(0, .01, N)
print("ADF sine with noise", calc_adf(sine, sine + noise))

　　（6）混入噪音后，会得到如下所示的结果。

ADF sine with noise (-17.189954017732465, 6.562246524247854e-30, 0, 308, 
{'1%': -3.45176116018037, '5%': -2.870970093607691, '10%': -2.571794416006072}, -1892.7915483183574)

　　P值出现明显下降。ADF指标的值为−17.19，低于字典中所有的临界值，所有这些都是拒绝协整的有力证据。

　　（7）下面生成一个幅值和偏移量更大的余弦波并混入噪音。

cosine = 100 * np.cos(t) + 10
print("ADF sine vs cosine with noise", calc_adf(sine, cosine + noise))

　　下面是我们得到的值。

ADF sine vs cosine with noise (-8.180271394419046, 8.166866117384127e-13, 16, 292, 
{'1%': -3.4529449243622383, '5%': -2.871489553425686, '10%': -2.572071437887033}, -10266.495772517574)

　　同样，证据有力地表明拒绝协整。正弦和太阳黑子之间的协整检验结果如下。

Sine vs sunspots (-6.724269181070093, 3.4210811915550897e-09, 16, 292, 
{'1%': -3.4529449243622383, '5%': -2.871489553425686, '10%': -2.572071437887033}, -1102.5867415291168)

　　这里所用的两个时间序列对的置信水平大体相当，都与数据点的数量有关，但是变化不大，总结见表7-1。

序列对/　　统计量/　　P值/　　5%/　　1%/　　10%/　　拒绝

正弦与正弦/　　−5.03E-16/　　0.95/　　−2.87/　　−3.45/　　−2.57/　　No

正弦与含噪声的正弦/　　−7.45/　　/5.58E-11　　−2.87/　　−3.45/　　−2.57/　　Yes

正弦与含噪声的余弦/　　−17.92/　　2.89E-30/　　−2.87/　　−3.45/　　−2.57/　　Yes

正弦与太阳黑子/　　−6.72/　　3.42E-09/　　−2.87/　　−3.45/　　−2.57/　　Yes

7.5自相关

 　　自相关是数据集内部的相关性，可用来指明趋势。

　　对于给定的时间序列，我们只要知道其均值和标准差，就可以用期望值算子来定义时间s和t的自相关。

 

　　本质上，这就是把相关性公式应用于一个时间序列及其同一个时间序列的滞后部分。

　　举例来说，如果后延一个周期，就可以检测前一个值是否影响当前值。当然，如果是真的，那么计算出的自相关的取值自然会相当高。

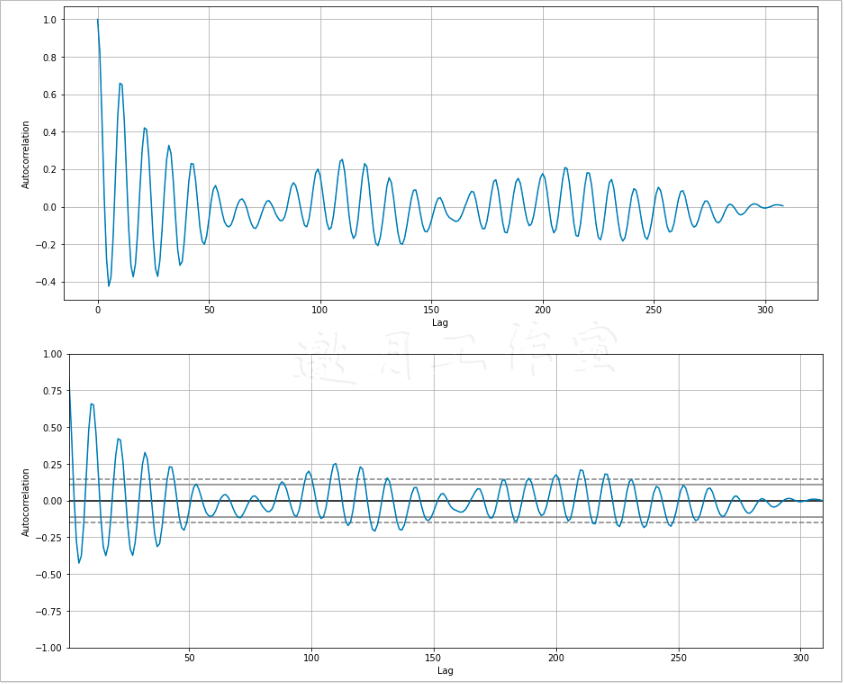
　　第6章曾经用Pandas函数绘制过自相关图形。本例中将使用NumPy库的correlate()函数来计算太阳黑子周期实际的自相关值。最后，对取得的数值进行正则化处理。

NumPy库的correlate()函数用法如下。

y = data - np.mean(data)
norm = np.sum(y ** 2)
correlated = np.correlate(y, y, mode='full')/norm

　　此外，我们对关联度最高值的索引也很感兴趣，这些索引可用NumPy的argsort()函数取得，它返回的是数组排序后对应的下标。

print(np.argsort(res)[-5:])

　　下面是自相关程度最高的值的下标。

[ 9 11 10 1 0]

　　自相关的最大值对应于零延迟，即信号与其自身的相关性；次最大值对应于一个周期的延迟，即10年。以下代码摘自本书代码包的ch-07.ipynb文件。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from pandas.plotting import autocorrelation_plot

data_loader = sm.datasets.sunspots.load_pandas()
data = data_loader.data["SUNACTIVITY"].values
y = data - np.mean(data)
norm = np.sum(y ** 2)
correlated = np.correlate(y, y, mode='full')/norm
res = correlated[int(len(correlated)/2):]

print(np.argsort(res)[-5:])
plt.plot(res)
plt.grid(True)
plt.xlabel("Lag")
plt.ylabel("Autocorrelation")
plt.show()
autocorrelation_plot(data)
plt.show()

　　最终结果如图7-3所示。可以将图7-3与下面Pandas绘制的图7-4做比较。

 

7.6自回归模型

 　　自回归模型可用于预测时间序列将来的值。使用该模型时，通常需要假定一个随机变量的值依赖于它前面的值。另外，该模型还假定前后值之间的关系是线性的，我们要做的就是拟合数据，以便给数据找到适当的参数。

　　自回归模型的数学公式如下。

 

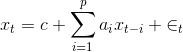
　　上面公式中，c是常量，最后一项是随机分量，又名白噪声。

　　这给我们提出了一个很常见的线性回归问题，但从实用性考虑，保持模型的简单性是十分重要的，因此我们只保留必要的滞后分量。按机器学习的专业术语来说，这些叫作特征。处理回归问题时，Python的机器学习库scikit-learn虽然不是最好的，也是一个上乘之选。第10章我们将会用到这个API。

　　进行回归分析时，我们常常遇到过拟合的问题，这个问题经常出现在对样本的拟合程度非常理想的情况下，这时一旦引入新的数据点，其表现立刻变差。对付这个问题的标准解决方案是进行交叉验证，或者使用没有过拟合问题的算法。利用这种方法，我们只将一部分样本用于模型参数的估算，其余数据用于该模型的测试和评估。这实际上是一种简化的解释，现实中有更复杂的交叉验证方案，其中很多已在scikit-learn中得到支持。为了评估该模型，我们需要计算适当的评价指标。这种评价指标不仅很多，而且随着从业人员对其理解的不断调整，指标的定义也在不断变化。我们可以借助书本或Wikipedia找到这些指标的定义，但是请记住，预测或者拟合的评估方法不是一门精确的科学。事实上，指标如此多，只能表明谁也说服不了谁。

　　下面我们通过scipy.optimize.leastsq()函数来搭建模型，该函数使用的前两个滞后分量我们在之前已经见过。此外，我们还可以选择一个线性代数函数作为替代。可是，leastsq()函数具有更大的灵活性，让我们几乎可以规定任意类型的模型。搭建模型的代码如下。

def model(p, x1, x10):
   p1, p10 = p
   return p1 * x1 + p10 * x10

def error(p, data, x1, x10):
   return data - model(p, x1, x10)

　　拟合模型时，我们需要给参数表赋初值并将其传递给leastsq()函数，具体如下。

def fit(data):
   p0 = [.5, 0.5]
   params = leastsq(error, p0, args=(data[10:], data[9:-1], 
data[:-10]))[0]
   return params

　　下面在部分数据上训练该模型。

cutoff = int(.9 * len(sunspots))
params = fit(sunspots[:cutoff])
print("Params", params)

　　以下是得到的参数。

Params [0.67172672 0.33626295]

　　有了这些参数，就可以绘出预测值并计算各个指标。下面是得到的指标值。

Root mean square error 22.8148122612597
Mean absolute error 17.651544650286237
Mean absolute percentage error 60.78178007359871
Symmetric Mean absolute percentage error 34.98433861762137
Coefficient of determination 0.7999402927786483

　　最终结果如图7-5所示。

 

　　许多预测看起来几乎命中，而另一些则相去甚远。总的来说，拟合效果不是很理想，但也不算很烂，介于两者之间。

　　以下代码摘自本书代码包中的ch-07.ipynb文件。

from scipy.optimize import leastsq
import statsmodels.api as sm
import matplotlib.pyplot as plt
import numpy as np

def model(p, x1, x10):
   p1, p10 = p
   return p1 * x1 + p10 * x10

def error(p, data, x1, x10):
   return data - model(p, x1, x10)

def fit(data):
   p0 = [.5, 0.5]
   params = leastsq(error, p0, args=(data[10:], data[9:-1], 
data[:-10]))[0]
   return params

data_loader = sm.datasets.sunspots.load_pandas()
sunspots = data_loader.data["SUNACTIVITY"].values

cutoff = int(.9 * len(sunspots))
params = fit(sunspots[:cutoff])
print("Params", params)

pred = params[0] * sunspots[cutoff-1:-1] + params[1] * sunspots[cutoff-10:-10]
actual = sunspots[cutoff:]
print("Root mean square error", np.sqrt(np.mean((actual - pred) ** 2)))
print("Mean absolute error", np.mean(np.abs(actual - pred)))
print("Mean absolute percentage error", 100 * 
np.mean(np.abs(actual - pred)/actual))
mid = (actual + pred)/2
print("Symmetric Mean absolute percentage error", 100 * 
np.mean(np.abs(actual - pred)/mid))
print("Coefficient of determination", 1 - ((actual - pred) ** 
2).sum()/ ((actual - actual.mean()) ** 2).sum())
year_range = data_loader.data["YEAR"].values[cutoff:]
plt.plot(year_range, actual, 'o', label="Sunspots")
plt.plot(year_range, pred, 'x', label="Prediction")
plt.grid(True)
plt.xlabel("YEAR")
plt.ylabel("SUNACTIVITY")
plt.legend()
plt.show()

7.7ARMA模型

 　　ARMA模型由自回归模型和移动平均模型结合而成，常用于时间序列的预测。使用移动平均模型时，我们通常假定随机变量为噪声分量的线性组合与时间序列的均值之和。

　提示：自回归模型和移动平均模型可以具有不同的阶数。一般来说，我们能够定义一个具有p个自回归项和q个移动平均项的ARMA模型，如下所示。

 

　　正如自回归模型公式那样，上面的公式中也含有常数部分和白噪声部分。然而，这里还要设法拟合后面的噪声部分。

　　幸运的是，我们可以使用statsmodelssm.tsa.ARMA()例程进行此类分析。下面使用ARMA(10,1)模型来拟合数据，代码如下。

model = sm.tsa.ARMA(df, (10,1)).fit()

　　我们进行预测（statsmodels模块使用了许多字符串）。

prediction = model.predict('1975', str(years[-1]), dynamic=True)

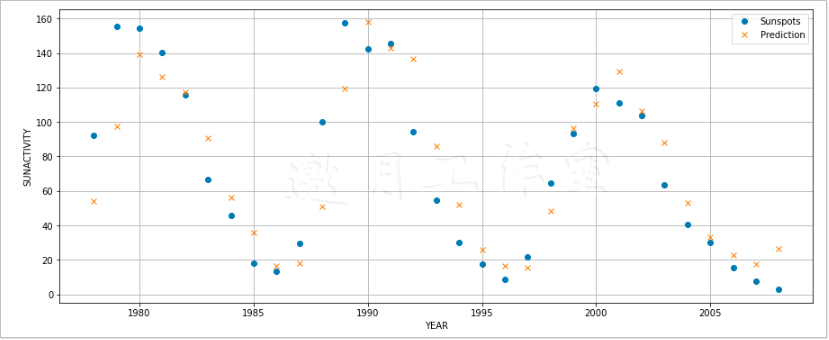
　　最终结果如图7-6所示。

　　坦白地说，拟合效果很差，原因是该模型对数据过拟合了。在7.6节中，这个简单模型的表现要更好一些。下面的示例代码摘自本书代码包中的ch-07.ipynb文件。

Import pandas as pd

Import matplotlib.pyplot as plt

Import statsmodels.api as sm

Import datetime

 

Data_loader = sm.datasets.sunspots.load_pandas()

import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import datetime

data_loader = sm.datasets.sunspots.load_pandas()
df = data_loader.data
years = df["YEAR"].values.astype(int)
df.index = pd.Index(sm.tsa.datetools.dates_from_range(str(years[0]), 
str(years[-1])))
del df["YEAR"]

model = sm.tsa.ARMA(df, (10,1)).fit()
prediction = model.predict('1975', str(years[-1]), dynamic=True)

df['1975':].plot()
prediction.plot(style='--', label='Prediction')
plt.legend()
plt.show()

 

7.8生成周期信号

 　　许多自然现象就像精确的时钟一样，具有规律性，并且值得信赖。而有些自然现象，则会表现出一些看上去非常规则的模式。通过希尔伯特-黄变换（Hilbert-Huang transform），一个科学家小组发现太阳黑子活动具有3个不同的周期。这3个周期的持续时间大致为11年、22年和100年。一般情况下，我们使用正弦函数之类的三角函数来模拟周期信号。当然，这些函数我们在中学时就学过了。对于本例来说，这些知识就足够了。因为这里有3个周期，所以看上去通过3个正弦函数线性组合成一个模型比较合理。这种方法只需要对自回归模型的代码稍作修改。下列代码摘自本书代码包中的periodic.py文件。

from scipy.optimize import leastsq
import statsmodels.api as sm
import matplotlib.pyplot as plt
import numpy as np
def model(p, t):
   C, p1, f1, phi1 , p2, f2, phi2, p3, f3, phi3 = p
   return C + p1 * np.sin(f1 * t + phi1) + p2 * np.sin(f2 * t + 
phi2) +p3 * np.sin(f3 * t + phi3)


def error(p, y, t):
   return y - model(p, t)

def fit(y, t):
   p0 = [y.mean(), 0, 2 * np.pi/11, 0, 0, 2 * np.pi/22, 0, 0, 2 * 
np.pi/100, 0]
   params = leastsq(error, p0, args=(y, t))[0]
   return params

data_loader = sm.datasets.sunspots.load_pandas()
sunspots = data_loader.data["SUNACTIVITY"].values
years = data_loader.data["YEAR"].values

cutoff = int(.9 * len(sunspots))
params = fit(sunspots[:cutoff], years[:cutoff])
print("Params", params)

pred = model(params, years[cutoff:])
actual = sunspots[cutoff:]
print("Root mean square error", np.sqrt(np.mean((actual - pred) ** 
2)))
print("Mean absolute error", np.mean(np.abs(actual - pred)))
print("Mean absolute percentage error", 100 * 
np.mean(np.abs(actual - pred)/actual))
mid = (actual + pred)/2
print("Symmetric Mean absolute percentage error", 100 * 
np.mean(np.abs(actual - pred)/mid))
print("Coefficient of determination", 1 - ((actual - pred) ** 
2).sum()/ ((actual - actual.mean()) ** 2).sum())
year_range = data_loader.data["YEAR"].values[cutoff:]
plt.plot(year_range, actual, 'o', label="Sunspots")
plt.plot(year_range, pred, 'x', label="Prediction")
plt.grid(True)
plt.xlabel("YEAR")
plt.ylabel("SUNACTIVITY")
plt.legend()
plt.show()

　　输出内容如下。

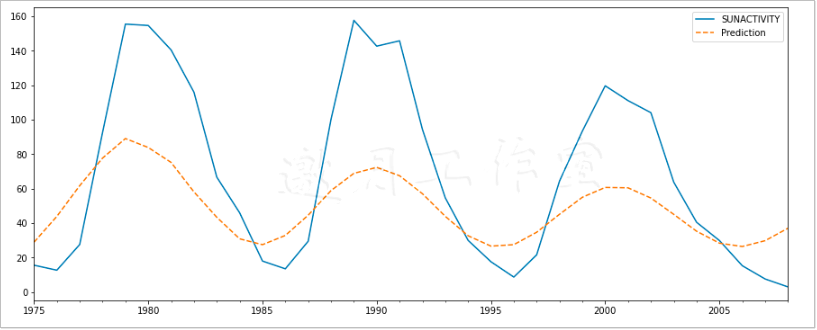
Params [ 47.18800335  28.89947427   0.56827284   6.51168781   4.55215008
   0.29372074 -14.30920341 -18.16523992   0.06574835  -4.37789699]
Root mean square error 59.561930255687216
Mean absolute error 44.581468315714496
Mean absolute percentage error 65.16404904506578
Symmetric Mean absolute percentage error 78.44776724314043
Coefficient of determination -0.36352579271706853

　　第一行展示的是模型的相关系数。这里的平均绝对误差是44，表示各个预测值与真实值之间平均相差多大。为了更好地拟合数据，判定系数应尽量接近1。可是，实际上得到的判定系数却是一个负值，这离我们的要求相去甚远。最终结果如图7-7　 所示。

7.9傅里叶分析

 　　傅里叶分析是建立在以数学家Joseph Fourier命名的傅里叶级数之上的一种数学方法。傅里叶级数是一种表示函数的数学方法，它通常使用正弦函数和余弦函数构成的无穷级数来表示函数。这些函数既可以是实值函数，也可以是虚值函数。

 

　　对于傅里叶分析来说，最高效的算法非快速傅里叶变换（Fast Fourier Transform，FFT）莫属。这个算法已经在SciPy与NumPy这两个库中实现了。

　　当应用于时间序列数据时，傅里叶分析能够将数据从时域映射到频域上面，从而得到一个频谱。对于某些频谱来说，它们会在频谱的特定频率上表现为一些尖峰。例如，乐谱就是由代表不同频率的音符构成的，其中A音符的声高为440Hz。实际上，A音符代表的就是敲击音叉时所产生的声音。借助钢琴之类的乐器，我们不仅可以演奏出A音符，还可以演奏出其他音符。白噪声是由许多不同频率的信号构成的，而且这些信号的功率一样。白光也是由不同频率的所有可见光混合而成的，这些可见光的功率也是一样的。

在下面的代码中，我们要导入两个函数（具体参阅ch-07.ipynb文件）。

from scipy.fftpack import rfft
from scipy.fftpack import fftshift

　　这里，rfft()函数可以对实值数据进行FFT。此外，我们还可以使用FFT()函数，但是它用于实值数据集时，会发出警告。函数fftshift()可以把零频分量（数据的平均值）移动到频谱中央，这样看起来会更舒服一些。为了便于理解，下面我们以正弦波为例进行讲解。首先，我们创建一个正弦波，然后对其实施FFT，具体代码如下。

t = np.linspace(-2 * np.pi, 2 * np.pi, len(sunspots))
mid = np.ptp(sunspots)/2
sine = mid + mid * np.sin(np.sin(t))

sine_fft = np.abs(fftshift(rfft(sine)))
print("Index of max sine FFT", np.argsort(sine_fft)[-5:])

　　下面输出的是对应于最大振幅的相应索引。

Index of max sine FFT [160 157 166 158 154]

　　我们对太阳黑子数据进行FFT。

transformed = np.abs(fftshift(rfft(sunspots)))
print("Indices of max sunspots FFT", np.argsort(transformed)[-5:])

　　通过下列索引我们可以看出，频谱中有5个大峰值。

Indices of max sunspots FFT [205 212 215 209 154]

　　我们看到，这里154处也有一个最大峰值。最终结果如图7-8所示。

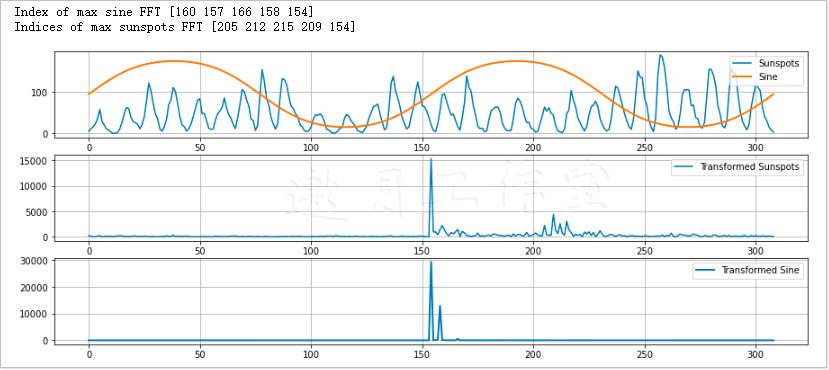
　　下面的代码摘自本书代码包中的ch-07.ipynb文件。

import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy.fftpack import rfft
from scipy.fftpack import fftshift

data_loader = sm.datasets.sunspots.load_pandas()
sunspots = data_loader.data["SUNACTIVITY"].values

t = np.linspace(-2 * np.pi, 2 * np.pi, len(sunspots))
mid = np.ptp(sunspots)/2
sine = mid + mid * np.sin(np.sin(t))

sine_fft = np.abs(fftshift(rfft(sine)))
print("Index of max sine FFT", np.argsort(sine_fft)[-5:])

transformed = np.abs(fftshift(rfft(sunspots)))
print("Indices of max sunspots FFT", np.argsort(transformed)[-5:])

plt.subplot(311)
plt.plot(sunspots, label="Sunspots")
plt.plot(sine, lw=2, label="Sine")
plt.grid(True)
plt.legend()
plt.subplot(312)
plt.plot(transformed, label="Transformed Sunspots")
plt.grid(True)
plt.legend()
plt.subplot(313)
plt.plot(sine_fft, lw=2, label="Transformed Sine")
plt.grid(True)
plt.legend()
plt.show()

7.10谱分析

 　　在7.9节中，我们绘制了数据集的振幅频谱。而物理信号的功率频谱可以直观展现出该信号的能量分布。对于前面的代码，我们稍作修改就能用来绘制功率频谱。具体做法是将某些值取平方，代码如下。

plt.plot(transformed ** 2, label="Power Spectrum")

　　相位谱可以为我们直观展示相位，即正弦函数的起始角，相应代码如下。

plt.plot(np.angle(transformed), label="Phase Spectrum")

　　最终结果如图7-9所示。

　　至于完整的代码，请读者参阅本书代码包中的ch-07.ipynb文件。

 

 

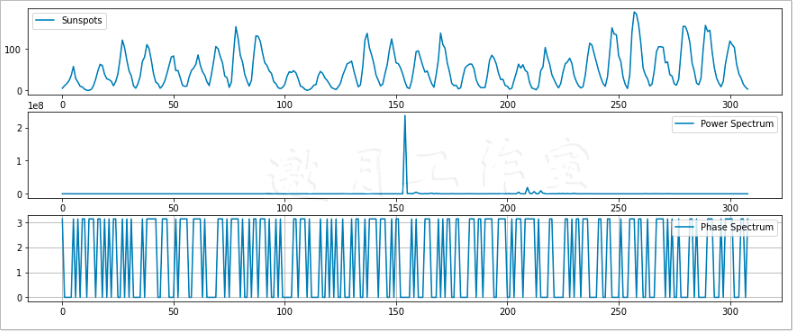
7.11滤波

 　　滤波是一种信号处理技术，可以对信号的某些部分进行删减或抑制。应用FFT后，我们就可以对高频或低频进行过滤或者设法删除白噪声了。白噪声是功率频谱为常数的一个随机信号，因此，它不包含任何有用信息。Scipy.Signal程序包为滤波提供了许多相应的实用程序。下面的例子将展示部分函数的使用方法。

• 中值滤波器（Median Filter）可以用来计算滚动窗口中数据的中值，这个滤波器是由medfilt()函数实现的，我们可以通过可选参数来指定窗口大小。
• Wiener滤波器能够通过统计数值来删除噪音，对于一个滤波器g(t)与一个信号s(t)，我们可以通过 (g * [s + n])(t)来计算其卷积。这个滤波器是通过wiener()实现的，它同样也有一个指定窗口大小的可选参数。
• Detrend滤波器可以用来删除趋势。它可以是一个线性或者不变趋势。这个滤波器是由detrend()函数实现的。

　　下列代码摘自本书代码包中的ch-07.ipynb文件。

import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy.signal import medfilt
from scipy.signal import wiener
from scipy.signal import detrend

data_loader = sm.datasets.sunspots.load_pandas()
sunspots = data_loader.data["SUNACTIVITY"].values
years = data_loader.data["YEAR"].values

plt.plot(years, sunspots, label="SUNACTIVITY")
plt.plot(years, medfilt(sunspots, 11), lw=2, label="Median")
plt.plot(years, wiener(sunspots, 11), '--', lw=2, label="Wiener")
plt.plot(years, detrend(sunspots), lw=3, label="Detrend")
plt.xlabel("YEAR")
plt.grid(True)
plt.legend()
plt.show()

　　最终结果如图7-10所示。

 

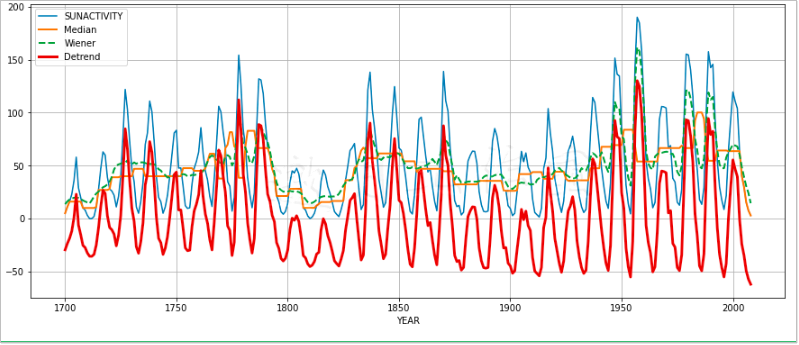
7.12小结

 　　本章的时间序列示例使用了年度太阳黑子周期数据。

　　我们介绍了一个比较常见的问题的解决方法，即在同一个时间序列中找出一个值与固定周期数之前的另一个数据点或者一组数据点之间的关系。

　　对于移动平均法，需要指定一个窗口来明确规定向前可以看到的数据，此后，窗口每一次前移一个周期，都要计算一次窗口内数据的平均值。在Pandas的应用程序接口中，rolling()函数为我们提供了许多窗口函数的功能，其中字符串参数win_type取不同的值，就对应不同的窗口函数。

　　协整类似于相关性，是一个度量两个时间序列之间的关系的指标。进行回归分析时，我们经常遇到过拟合的问题。这个问题表现为，模型对于样本拟合的效果非常理想，但是当引入新数据点后，效果却变得很糟糕。为了对模型进行评估，我们可以求取适当的评价指标。

　　对于数据分析而言，数据库是一个非常重要的工具。自从20世纪70年代开始，关系型数据库便开始流行起来。现在，NoSQL数据库已经变成一个可行的替代方案。第8章将会介绍各种相关的数据库（包括关系型与NoSQL数据库）及其应用程序接口。

 

第7章完。

python数据分析个人学习读书笔记-目录索引

 

随书源码官方下载：
https://www.ptpress.com.cn/shopping/buy?bookId=bae24ecb-a1a1-41c7-be7c-d913b163c111

需要登录后免费下载。