《python数据分析（第2版）-阿曼多.凡丹戈》读书笔记第4章-统计学与线性代数

python数据分析个人学习读书笔记-目录索引

第4章统计学与线性代数

　　统计学和线性代数为探索性数据分析奠定了基础。无论是描述性还是推论性的统计方法，都有助于从原始数据中获得见解和进行推断。比如，通过数据求出变量的算术平均值和标准差，并由此推出该变量的取值范围和期望值后，我们就可以利用统计检验来评估所得结论的可信度了。

　　线性代数关注的是解线性方程组，而NumPy和SciPy的linalg程序包可以帮我们轻松地解决这个问题。线性代数用途广泛，如利用模型拟合数据时就离不开它。除此之外，本章还会介绍其他几种NumPy和SciPy程序包，内容涉及随机数的生成和掩码式数组（Masked arrays）。

　　本章涉及以下主题。

• 利用NumPy处理简单的描述性统计运算
• 利用NumPy进行线性代数运算
• 利用NumPy寻找特征值和特征向量
• NumPy随机数
• 创建NumPy掩码式数组（Masked arrays）

 

4.1用NumPy进行简单的描述性统计计算

 　　在本书中，我们会尽量使用各种不同的可以通过公开渠道获得的数据集。但是，这些数据的主题未必正是读者的兴趣之所在。此外，虽然每个数据集都有其自身的特点，但是本书介绍的技巧却是通用的，所以同样适用于大家的领域。在本章中，我们将数据集从statsmodels库载入NumPy数组，来进行数据分析。

　　Mauna Loa CO2测量数据是我们用到的statsmodels库的第一个数据集。以下代码将会加载数据集并给出基本的描述性统计值。

import numpy as np
from scipy.stats import scoreatpercentile
import pandas as pd

data = pd.read_csv("co2.csv", index_col=0, parse_dates=True)

co2 = np.array(data.co2)

print("The statistical valus for amounts of co2 in atmosphere : \n")
print("Max method : ", co2.max())
print("Max function : ", np.max(co2))

print("Min method : ", co2.min())
print("Min function : ", np.min(co2))

print("Mean method : ", co2.mean())
print("Mean function : ", np.mean(co2))

print("Std method : ", co2.std())
print("Std function : ", np.std(co2))

print("Median : ", np.median(co2))
print("Score at percentile 50 : ", scoreatpercentile(co2, 50))

　　上面的代码会计算NumPy数组的平均值、中位数、最大值、最小值以及标准差。

　　Tips:如果这些术语听起来不太熟悉，不妨花些时间到维基百科或其他地方了解一下相关内容。前言部分讲过，本书假设读者熟悉基本的数学和统计概念。

　　这里使用的数据来自statsmodels包，这些都是美国夏威夷Mauna Loa天文台观测到的大气CO2的值。

　　现在，我们来看看具体代码。

　　（1）     首先，使用import语句来加载Python包的相关模块，具体如下。

import numpy as np
from scipy.stats import scoreatpercentile
import pandas as pd

　　（2）然后，调用下面的函数来加载数据。

data = pd.read_csv("co2.csv", index_col=0, parse_dates=True)

co2 = np.array(data.co2)

　　上述代码中的数据将被复制到NumPy数组co2中，该数组用来存放大气中CO2的观测值。

　　（3）数组的最大值可以通过ndarray的方法或者其他的NumPy函数来获得，另外最小值、平均值和标准差同样如此。下列代码将会显示各种统计指标。

print("The statistical valus for amounts of co2 in atmosphere : \n")
print("Max method : ", co2.max())
print("Max function : ", np.max(co2))

print("Min method : ", co2.min())
print("Min function : ", np.min(co2))

print("Mean method : ", co2.mean())
print("Mean function : ", np.mean(co2))

print("Std method : ", co2.std())
print("Std function : ", np.std(co2))

　　输出内容如下。

Max method :  366.84
Max function :  366.84
Min method :  313.18
Min function :  313.18
Mean method :  337.0535256410256
Mean function :  337.0535256410256
Std method :  14.950221626197369
Std function :  14.950221626197369

　　（4）中位数（median）可以用NumPy或者SciPy的函数得到。下列代码将计算数据第50百分位数。

print("Median : ", np.median(co2))
print("Score at percentile 50 : ", scoreatpercentile(co2, 50))

　　以下是输出内容。

Median :  335.17
Score at percentile 50 :  335.17

 

4.2用NumPy进行线性代数运算

 　　线性代数是数学的一个重要分支，比如，我们可以使用线性代数来解决线性回归问题。子程序包numpy.linalg提供了许多线性代数例程，我们可以用它来计算矩阵的逆或特征值，求解线性方程或计算行列式等。对于NumPy来说，矩阵可以用ndarray的一个子类来表示。

4.2.1　用NumPy求矩阵的逆

 　　在线性代数中，假设A是一个方阵或可逆矩阵，如果存在一个矩阵A-1，满足矩阵A-1与原矩阵A相乘后等于单位矩阵I这一条件，那么就称矩阵A-1是A的逆，相应的数学方程如下。

　　A A^-1 = I

　　子程序包numpy.linalg中的inv()函数就是用来求矩阵的逆的。下面通过一个例子进行说明，具体步骤如下。

　　（1）利用mat()函数创建一个示例矩阵。

A = np.mat("2 4 6;4 2 6;10 -4 18")
print("A\n", A)

　　矩阵A的内容如下。

A
 [[ 2  4  6]
 [ 4  2  6]
 [10 -4 18]]

　　（2）求矩阵的逆。现在可以利用inv()子例程来计算逆矩阵了。

inverse = np.linalg.inv(A)
print("inverse of A\n", inverse)

　　逆矩阵显示如下。

inverse of A
 [[-0.41666667  0.66666667 -0.08333333]
 [ 0.08333333  0.16666667 -0.08333333]
 [ 0.25       -0.33333333  0.08333333]]

　　Tips：如果该矩阵是奇异的，或者非方阵，那么我们就会得到LinAlgError消息。如果愿意，我们也可以通过手动来验证这个计算结果。NumPy库中的pinv()函数可以用来求伪逆矩阵，它适用于任意矩阵，包括非方阵。

　　（3）利用乘法进行验算。

　　下面我们将inv()函数的计算结果乘以原矩阵，验算结果是否正确。

print("Check\n", A * inverse)

　　不出我们所料，果然得到了一个单位矩阵（当然，前提是一些小误差忽略不计）。

Check
 [[ 1.00000000e+00  1.11022302e-16 -2.77555756e-17]
 [-2.22044605e-16  1.00000000e+00 -2.77555756e-17]
 [-8.88178420e-16  1.22124533e-15  1.00000000e+00]]

　　我们将上面的计算结果减去3×3的单位矩阵，会得到求逆过程中出现的误差。

print("Error\n", A * inverse - np.eye(3))

　　一般来说，这些误差通常忽略不计，但是在某些情况下，细微的误差也可能导致不良后果。

Error
 [[-1.11022302e-16  1.11022302e-16 -2.77555756e-17]
 [-2.22044605e-16  4.44089210e-16 -2.77555756e-17]
 [-8.88178420e-16  1.22124533e-15 -2.22044605e-16]]

　　这种情况下，我们需要使用精度更高的数据类型，或者更高级的算法。前面我们使用了numpy.linalg子程序包的inv()例程来计算矩阵的逆。下面，我们用矩阵乘法来验证这个逆矩阵是否符合我们的要求。

import numpy as np
A = np.mat("2 4 6;4 2 6;10 -4 18")
print "A\n", A

inverse = np.linalg.inv(A)
print("inverse of A\n", inverse)

print("Check\n", A * inverse)
print("Error\n", A * inverse - np.eye(3))

 

4.2.2　用NumPy解线性方程组

 　　矩阵可以通过线性方式把一个向量变换成另一个向量，因此从数值计算的角度看，这种操作对应于一个线性方程组。Numpy.linalg中的solve()子例程可以求解类似Ax = b这种形式的线性方程组，其中A是一个矩阵，b是一维或者二维数组，而x是未知量。下面我们介绍如何使用dot()函数来计算两个浮点型数组的点积（dot product）。

　　这里举例说明解线性方程组的过程，具体步骤如下。

　　（1）首先创建矩阵A和数组b。

　　用于创建矩阵A和数组b代码如下。

A = np.mat("1 -2 1;0 2 -8;-4 5 9")
print("A\n", A)

b = np.array([0, 8, -9])
print("b\n", b)

　　矩阵A和数组（向量）b的定义如下所示。

A
 [[ 1 -2  1]
 [ 0  2 -8]
 [-4  5  9]]
b
 [ 0  8 -9]

　　（2）调用solve()函数。

　　（3）接下来，用solve()函数来解这个线性方程组。

x = np.linalg.solve(A, b)
print("Solution", x)

　　线性方程组的解如下。

Solution [29. 16.  3.]

　　（4）我们利用dot()函数进行验算。

　　我们利用dot()函数验算这个解是否正确。

print("Check\n", np.dot(A , x))

　　结果不出所料。

Check[[ 0. 8. -9.]]

　　前面，我们通过NumPy的linalg子程序包中的solve()函数求出了线性方程组的解，而且利用dot()函数验算了结果，下面我们把这些代码放到一起。

import numpy as np

A = np.mat("1 -2 1;0 2 -8;-4 5 9")
print("A\n", A)

b = np.array([0, 8, -9])
print("b\n", b)

x = np.linalg.solve(A, b)
print("Solution", x)

print("Check\n", np.dot(A , x))

 

 

4.3用NumPy计算特征值和特征向量

 　　特征值是方程式Ax=ax的标量解（scalar solutions），其中A是一个二维矩阵，而x是一维向量。特征向量实际上就是表示特征值的向量。

　　Tips：特征值和特征向量都是基本的数学概念并且常用于一些重要的算法中，如主成分分析（PCA）算法。PCA可以极大地简化大规模数据集的分析过程。

　　计算特征值时，我们可以求助于numpy.linalg程序包提供的eigvals()子例程。函数eig()的返回值是一个元组，其元素为特征值和特征向量。

　　我们可以用子程序包numpy.linalg的eigvals()和eig()函数来获得矩阵的特征值和特征向量，同时通过dot()函数来验算结果。

import numpy as np
A = np.mat("3 -2;1 0")
print("A\n", A)

print("Eigenvalues", np.linalg.eigvals(A))

eigenvalues, eigenvectors = np.linalg.eig(A)
print("First tuple of eig", eigenvalues)
print("Second tuple of eig\n", eigenvectors)

for i in range(len(eigenvalues)):
   print("Left", np.dot(A, eigenvectors[:,i]))
   print("Right", eigenvalues[i] * eigenvectors[:,i])

　　下面来计算一个矩阵的特征值。

　　（1）我们创建矩阵。

　　（2）下列代码将创建一个矩阵。

A = np.mat("3 -2;1 0")
print("A\n", A)

　　下面的矩阵即刚才创建的矩阵。

A
 [[ 3 -2]
 [ 1  0]]

　　（2）利用eig()函数计算特征值。

　　这时，我们可以使用eig()子例程。

Print(“Eigenvalues”, np.linalg.eigvals(A))

　　该矩阵的特征值如下。

Eigenvalues [2. 1.]

　　（3）利用eig()函数取得特征值和特征向量。

　　利用eig()函数，可以得到特征值和特征向量。注意，该函数返回的是一个元组，它的第1个元素是特征值，第2个元素为相应的eigenvectors，以面向列的方式排列。

eigenvalues, eigenvectors = np.linalg.eig(A)
print("First tuple of eig", eigenvalues)
print("Second tuple of eig\n", eigenvectors)

　　特征值eigenvalues和特征向量eigenvectors的值分别如下。

First tuple of eig [2. 1.]
Second tuple of eig
 [[0.89442719 0.70710678]
 [0.4472136  0.70710678]]

　　（4）验算结果。

　　通过dot()函数计算特征值方程式Ax = ax两边的值，我们就可以对结果进行验算。

for i in range(len(eigenvalues)):
   print("Left", np.dot(A, eigenvectors[:,i]))
   print("Right", eigenvalues[i] * eigenvectors[:,i])

　　输出内容如下。

Left [[1.78885438]
 [0.89442719]]
Right [[1.78885438]
 [0.89442719]]
Left [[0.70710678]
 [0.70710678]]
Right [[0.70710678]
 [0.70710678]]

 

4.4NumPy随机数

 　　随机数常用于蒙特卡罗法、随机积分等方面。然而，真正的随机数很难获得，实际中使用的都是伪随机数。大部分情况下，伪随机数就足以满足我们的需求。当然，某些特殊情况除外，例如进行高精度的模拟实验时。对于NumPy，与随机数有关的函数都在random子程序包中。

　　提示:NumPy核心的随机数发生器是基于梅森旋转算法的。

　　我们既可以生成连续分布的随机数，也可以生成非连续分布的随机数。分布函数有一个可选的size参数，它能通知NumPy要创建多少个数字。我们可以用整型或者元组来给这个参数赋值，这时会得到相应形状的数组，其值由随机数填充。离散分布包括几何分布、超几何分布和二项式分布。连续分布包括正态分布和对数正态分布。

4.4.1　用二项式分布进行博弈

 　　二项式分布模拟的是在进行整数次独立实验中成功的次数，其中每次实验的成功机会是一定的。

　　假设我们身在17世纪，正在对8片币玩法下注。当时流行用9枚硬币来玩。如果人头朝上的硬币少于5枚，那么我们将输掉一个8分币；否则，我们就赢一个8分币。下面，我们开始模拟这个游戏，假设我们手上有1000硬币作为初始备资。我们将使用random模块提供的binomial()函数进行模拟。

　Tips：完整的代码详见本书代码包中的ch-04.ipynb文件。

import numpy as np
from matplotlib.pyplot import plot, show

cash = np.zeros(10000)
cash[0] = 1000
outcome = np.random.binomial(9, 0.5, size=len(cash))

for i in range(1, len(cash)):

   if outcome[i] < 5:
      cash[i] = cash[i - 1] - 1
   elif outcome[i] < 10:
      cash[i] = cash[i - 1] + 1
   else:
      raise AssertionError("Unexpected outcome " + outcome)

print(outcome.min(), outcome.max())

plot(np.arange(len(cash)), cash)
show()

　　如果要了解binomial()函数，请看以下步骤。

　　（1）我们用binomial()函数。

　　我们将数组初始化为零，即现金余额为零。调用binomial()函数，将size参数设为10 000，这就表示我们要掷10 000次硬币。

cash = np.zeros(10000)
cash[0] = 1000
outcome = np.random.binomial(9, 0.5, size=len(cash))

　　（2）更新现金余额。

　　我们利用抛郑硬币的结果来更新cash数组，显示outcome数组中的最大值和最小值，只要保证没有罕见的异常值即可。

for i in range(1, len(cash)):

   if outcome[i] < 5:
      cash[i] = cash[i - 1] - 1
   elif outcome[i] < 10:
      cash[i] = cash[i - 1] + 1
   else:
      raise AssertionError("Unexpected outcome " + outcome)

print(outcome.min(), outcome.max())

不出所料，值为0～9。

0 9

　　（3）用matplotlib绘出cash数组的图像。

Plot(np.arange(len(cash)), cash)
Show()

　　从图４-2可以看出，现金余额的曲线类似于随机行走（即不按照固定模式，而是随机游走）。

 

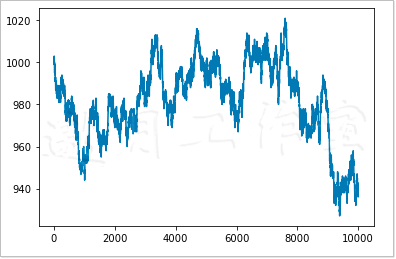
　　当然，我们每一次执行程序代码，都会得到一个不同的随机游走。如果想总是得到相同的结果，需要给NumPy的随机数子程序包中的binomial()函数一个种子值。

4.4.2　正态分布采样

 　　连续分布是通过概率密度函数（PDF）进行建模的。在特定区间发生某事件的可能性可以通过概率密度函数的积分运算求出。NumPy的random模块提供了许多表示连续分布的函数，如beta、chisquare、exponential、f、gamma、gumbel、laplace、lognormal、logistic、multivariate_normal、noncentral_chisquare、noncentral_f、normal等。

　　利用NumPy的random子程序包中的normal()函数，可以把正态分布以直观的形式图示出来。下面给出随机产生的数值的钟形曲线和条形图。

import numpy as np
import matplotlib.pyplot as plt

N=10000

normal_values = np.random.normal(size=N)
#dummy, bins, dummy = plt.hist(normal_values, int(np.sqrt(N)), normed =True, lw=1)
#normed：布尔值。官方不推荐使用，建议改用density参数。
dummy, bins, dummy = plt.hist(normal_values, int(np.sqrt(N)), density =True, lw=1)
sigma = 1
mu = 0
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) ),lw=2)
plt.show()

 

　　随机数可以按照正态分布的要求生成，它们的分布情况可以用条形图来显示。如果要绘制正态分布，请执行以下步骤。

　　（1）生成数值。

　　借助于NumPy的random子程序包提供的normal()函数，可以创建指定数量的随机数。

N=10000

normal_values = np.random.normal(size=N)

　　（2）画出条形图和理论上的PDF。

　　下面使用matplotlib来绘制条形图和理论上的PDF，这里中心值为0，标准差为1。

#dummy, bins, dummy = plt.hist(normal_values, int(np.sqrt(N)), normed =True, lw=1)
#normed：布尔值。官方不推荐使用，建议改用density参数。
dummy, bins, dummy = plt.hist(normal_values, int(np.sqrt(N)), density =True, lw=1)
sigma = 1
mu = 0
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) ),lw=2)
plt.show()

　　图4-3为我们展示了著名的钟形曲线。

 

 

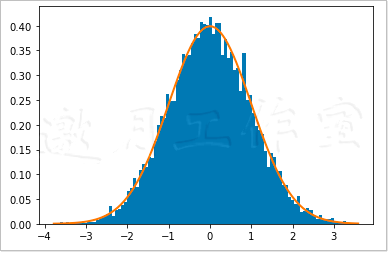
4.4.3　用SciPy进行正态检验

 　　正态分布被广泛用于科学和统计学领域，按照中心极限定理，随着独立观测的随机样本数量的增加，它们会趋向呈正态分布。正态分布的特性已经为大家所熟知，并且它还非常便于使用。不过，它需要满足许多必要条件，例如数据点的数量要足够大，同时还要求这些数据点必须是相互独立的。工作中，我们需要养成检查数据是否符合正态分布的好习惯。正态检验的方法有很多，有一些已经在scipy.stats程序包中实现了。本节将用到这些检验方法，样本是取自Google网站的流感趋势数据。这里我们对原始文件进行了简化处理，只留下日期和来自阿根廷的数据两列，下面给出示例行。

　　这些数据可以在本书代码包中的goog_flutrends.csv文件中找到，和前面一样，这里我们也按照正态分布对这些数据进行抽样。得到数组的大小与流感趋势数组相同，如果顺利通过正态检验，就以它为金标准（the golden standard）。这里的代码取自代码包中的ch-04.ipynb文件。

import numpy as np
from scipy.stats import shapiro
from scipy.stats import anderson
from scipy.stats import normaltest

flutrends = np.loadtxt("goog_flutrends.csv", delimiter=',', usecols=(1,), skiprows=1, converters = {1: lambda s: float(s or 0)}, unpack=True)
N = len(flutrends)
normal_values = np.random.normal(size=N)
zero_values = np.zeros(N)

print("Normal Values Shapiro", shapiro(normal_values))
#print("Zeroes Shapiro", shapiro(zero_values))
print("Flu Shapiro", shapiro(flutrends))

print("Normal Values Anderson", anderson(normal_values))
#print("Zeroes Anderson", anderson(zero_values))
print("Flu Anderson", anderson(flutrends))

print("Normal Values normaltest", normaltest(normal_values))
#print("Zeroes normaltest", normaltest(zero_values))
print("Flu normaltest", normaltest(flutrends))

　　作为一个反面例子，下面使用的这个数组跟前面提到的填满零的数组具有同样的大小。实际上，当处理一些小概率事件（如世界性疫情的爆发）时，就可能遇到这种数据。

在这个数据文件中，一些单元是空的。当然，这种问题经常会碰到，所以我们必须习惯于首先清洗数据。我们假定正确的数值是零，下面使用一个转换器来填上这些零值。

见上述代码第6行

　　夏皮罗-威尔克检验法可以对正态性进行检验。相应的SciPy函数将返回一个元组，其中第1个元素是一个检验统计量，第2个数值是p值。需要注意的是，这种填满了零的数组会引发警告。事实上，本例中用到的3个函数在处理这个数组方面确实有困难，同时还会引发警告。下面是得到的结果。

Normal Values Shapiro (0.9963182806968689, 0.18643833696842194)
Flu Shapiro (0.9351990818977356, 2.2945883254311397e-15)

　　这里得到的p值类似于本例中后面的第3个检验的结果。分析结果基本上是一样的。

　　Anderson-Darling检验可以用来检验正态分布以及其他分布，如指数分布、对数分布和冈贝尔（Gumbel）分布等。相关的SciPy函数涉及一个检验统计量和一个数组，该数组存放了15、10、5、2.5和1等百分值所对应的临界值。如果该统计量大于显著性水平的临界值，我们就可以断定它不具有正态性。我们将得到下列数值。

Normal Values Anderson AndersonResult(statistic=0.5299815280259281, critical_values=array([0.572, 0.652, 0.782, 0.912, 1.085]), significance_level=array([15. , 10. ,  5. ,  2.5,  1. ]))
Flu Anderson AndersonResult(statistic=8.258614154768793, critical_values=array([0.572, 0.652, 0.782, 0.912, 1.085]), significance_level=array([15. , 10. ,  5. ,  2.5,  1. ]))

　　对于这种用零填充的数组，我们没有什么好说的，因为返回的统计量根本就不是一个数值。就像我们期望的那样，这个金标准数组是符合正态分布的。然而，流感趋势数据返回的这个统计量大于所有的有关临界值，因此我们可以肯定它不符合正态分布。这3个测试函数中，这个看起来是最容易使用的一个。

　　SciPy的normaltest()函数还实现了D’Agostino检验和Pearson检验功能。该函数返回的元组和shapiro()函数一样，也包括一个统计量和p值。这里的p值是双边卡方概率（two-sided Chi-squared probability），卡方分布是另一种著名的分布，这种检验本身基于偏度和峰度检验的z分数。偏度系数用来表示分布的对称程度。因为正态分布是对称的，所以偏度系数为零。峰度系数描述的是分布的形状（尖峰、肥尾）。这种正态分布的峰度系数为3，超额峰度的系数为0。以下是本次检验获得的数值。

Normal Values normaltest NormaltestResult(statistic=3.8850841487225543, pvalue=0.14333910757583423)
Flu normaltest NormaltestResult(statistic=99.64373336356954, pvalue=2.304826411536872e-22)

　　因为这里处理的是p值的概率，所以它越大越好，最好接近1。对于这种用零填充的数组，会得到很奇怪的结果。不过，因为我们已经得到提示，所以对于这个特殊数组来说，结果是不可信的。此外，如果p值大于等于0.5，我们则认为它具有正态性。对于金标准数组，我们会得到一个更小的数值，这说明我们需要进行更多的观察。这一点作为作业，请读者自行练习。

 

4.5创建掩码式NumPy数组

 　　数据常常是凌乱的，而且含有空白项或者无法处理的字符，好在掩码式数组可以忽略残缺的或无效的数据点。Numpy.ma子程序包提供的掩码式数组隶属于ndarray，带有一个掩码。本节我们以Lena Soderberg的相片为数据源，而且假设某些数据已被破坏。下面是处理掩码式数组的完整代码，取自本书代码包中的ch – 04.ipynb文件。

import numpy
import scipy
import matplotlib.pyplot as plt

face = scipy.misc.face()

random_mask = numpy.random.randint(0, 2, size=face.shape)

plt.subplot(221)
plt.title("Original")
plt.imshow(face)
plt.axis('off')

masked_array = numpy.ma.array(face, mask=random_mask)

plt.subplot(222)
plt.title("Masked")
plt.imshow(masked_array)
plt.axis('off')

plt.subplot(223)
plt.title("Log")
plt.imshow(numpy.ma.log(face).astype("float32"))
plt.axis('off')


plt.subplot(224)
plt.title("Log Masked")
plt.imshow(numpy.ma.log(masked_array).astype("float32"))
plt.axis('off')

plt.show()

　　最后，我们来展示原图、原图的对数值、掩码式数组及其对数值。

　　（1）创建一个掩码。

　　为了得到一个掩码式数组，必须规定一个掩码。下面将生成一个随机掩码，这个掩码的取值非0即1。

Random_mask = numpy.random.randint(0, 2, size=face.shape)

　　（2）创建一个掩码式数组。

　　下面应用该掩码来创建一个掩码式数组。

Masked_array = numpy.ma.array(face, mask=random_mask)

　　我们得到的图4-4。

　　我们给NumPy数组附加了一个随机掩码，这样，与该掩码相对应的数据就会被忽略不计。Numpy.ma子程序包为处理掩码式数组提供了各种所需的函数，这里我们只介绍如何生成掩码式数组。

4.6忽略负值和极值

 　　当希望忽略负值，例如对数组的值取对数时，掩码式数组将会非常有用；此外，剔除异常值时，我们也会用到掩码式数组。这项工作是以极值的上下限为基础的。下面我们以来源于美国职业棒球大联盟（MLB）选手的薪金数据为例，来说明这些技术的应用方法。经过编辑，这份数据仅保留了选手姓名和薪金两栏，结果放在MLB2008.csv文件中，读者可以从本书代码包中找到。

　　至于完整的脚本，请参见本书代码包中的ch-04.ipynb文件。

import numpy as np
from datetime import date
import sys
import matplotlib.pyplot as plt

salary = np.loadtxt("MLB2008.csv", delimiter=',', usecols=(1,), skiprows=1, unpack=True)
triples = np.arange(0, len(salary), 3)
print("Triples", triples[:10], "...")

signs = np.ones(len(salary))
print("Signs", signs[:10], "...")

signs[triples] = -1
print("Signs", signs[:10], "...")

ma_log = np.ma.log(salary * signs)
print("Masked logs", ma_log[:10], "...")

dev = salary.std()
avg = salary.mean()
inside = np.ma.masked_outside(salary, avg - dev, avg + dev)
print("Inside", inside[:10], "...")

plt.subplot(311)
plt.title("Original")
plt.plot(salary)

plt.subplot(312)
plt.title("Log Masked")
plt.plot(np.exp(ma_log))

plt.subplot(313)
plt.title("Not Extreme")
plt.plot(inside)

plt.subplots_adjust(hspace=.9)

plt.show()

　　以下是对上述命令的说明。

　　（1）对负数取对数

　　我们可以对含有负数的数组取对数。首先创建一个数组，存放可以被3整除的数组。

triples = np.arange(0, len(salary), 3)
print("Triples", triples[:10], "...")

　　然后生成一个元素值全为1且大小与薪金数据数组相等的数组。

signs = np.ones(len(salary))
print("Signs", signs[:10], "...")

　　借助于第2章中学到的技巧，可以将下标是3的倍数的数组元素的值取反。

signs[triples] = -1
print("Signs", signs[:10], "...")

　　最终就可以对这个数组取对数了。

ma_log = np.ma.log(salary * signs)
print("Masked logs", ma_log[:10], "...")

　　下面显示相应的薪金数据（注意，这里有一些数据的值为NaN）。

Triples [ 0  3  6  9 12 15 18 21 24 27] ...
Signs [1. 1. 1. 1. 1. 1. 1. 1. 1. 1.] ...
Signs [-1.  1.  1. -1.  1.  1. -1.  1.  1. -1.] ...
Masked logs [-- 14.970818190308929 15.830413578506539 -- 13.458835614025542
 15.319587954740548 -- 15.648092021712584 13.864300722133706 --] ...

　　（2）忽略极值

　　此处规定：所谓异常值，就是在平均值一个标准差以下或者在平均值一个标准差以上的那些数值（这个定义未必恰当，只是为了便于计算）。根据上面的定义，可以利用下面的代码来屏蔽极值点。

dev = salary.std()
avg = salary.mean()
inside = np.ma.masked_outside(salary, avg - dev, avg + dev)
print("Inside", inside[:10], "...")

　　以下代码将显示前10个元素。

Inside [3750000.0 3175000.0 7500000.0 3000000.0 700000.0 4500000.0 3000000.0
 6250000.0 1050000.0 4600000.0] ...

　　下面分别绘制原始薪金数据、取对数后的数据和取幂复原后的数据，最后是应用基于标准差的掩码之后的数据。

　　具体如图4-5所示。

 

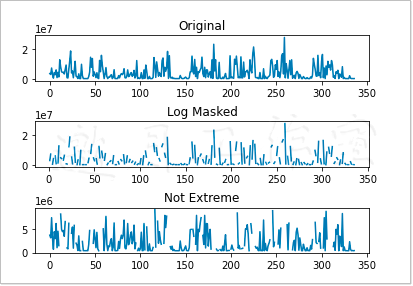
Numpy.ma子程序包中的函数可以屏蔽数组中被视为无效的元素，例如无法应用log()和sqrt()函数的负值元素。被屏蔽的值类似于关系数据库和程序设计中的NULL值，对被屏蔽的值进行运算时，给它的都是一个屏蔽后的值。

 

 4.7小结

 　　本章我们学习了多种NumPy和SciPy子库，回顾了线性代数、统计学、连续和离散分布、掩码式数组和随机数方面的内容。

　　第5章将介绍更多的技巧，尽管有人可能认为那些工作不算是数据分析。实际上，凡是能够与数据分析扯上关系的东西，我们都需要关注。通常，我们进行数据分析时，并不是在人员配备齐全的团队中工作，所以没人来替我们检索和存储数据。但是，如果要想顺畅地完成数据分析流程，这些工作又是不可或缺的，所以第5章会对这些工作进行详尽的说明。

 

 

第4章完。

python数据分析个人学习读书笔记-目录索引

 

随书源码官方下载：
https://www.ptpress.com.cn/shopping/buy?bookId=bae24ecb-a1a1-41c7-be7c-d913b163c111

需要登录后免费下载。