《python数据分析（第2版）-阿曼多.凡丹戈》读书笔记第2章-Numpy和数组
阿曼多·凡丹戈（Armando Fandango）的《python数据分析（第2版）》，2018年6月出版，本系列为读书笔记。主要是为了系统整理，加深记忆。 第2章“NumPy数组”介绍NumPy和数组的基础知识。通过阅读本章，读者能够基本掌握NumPy数组及其相关函数。
第2章“NumPy数组”介绍NumPy和数组的基础知识。通过阅读本章，读者能够基本掌握NumPy数组及其相关函数。
本章涉及的主题如下。
- NumPy数组对象
- 创建多维数组
- 选择NumPy数组元素
- NumPy数值类型
- 一维切片和索引
- 改变阵列形状
- 创建阵列视图和副本
- 花式索引
- 使用位置列表进行索引
- 用布尔值索引NumPy数组
- NumPy数组的广播技术
2.1NumPy数组对象
NumPy提供了一个名为ndarray的多维数组对象。NumPy数组是具有固定大小的类型化数组。Python的列表是异构的，因此列表的元素可以包含任何对象类型，而NumPy数组是同质的，只能存放同一种类型的对象。数组由两部分组成，分别如下。
- 存储在连续的内存块中的实际数据
- 描述实际数据的元数据
实际数据存储在连续的内存块中，因此当大型数据集作为ndarray进行加载时，我们就要看有没有足够多的连续内存块了。NumPy中的大部分数组方法和函数都不会直接修改实际数据，而只能修改元数据。
在之前的章节中，我们曾经用arange()函数来生成数组。实际上，那是用来存放一组数值的一维数组，这里的ndarray则可以具有一个以上的维度。
NumPy数组的优势
NumPy数组通常是同质的（有一种特殊的记录数组类型，它可以是异质的），即数组中的数据项的类型必须一致。NumPy数组元素类型一致的好处是：因为知道数组元素的类型相同，所以能轻松确定存储数组所需空间的大小。同时，NumPy数组还能够运用向量化运算来处理整个数组；而完成同样的任务，Python的列表则通常需要借助循环语句遍历列表并对逐个元素进行相应的处理。NumPy数组的索引方法与Python类似，下标从0开始。此外，NumPy使用了优化过的C API，所以运算速度格外快。
今后，我们会经常利用arange()子例程来建立数组。通常，向量就是一个一维数组。
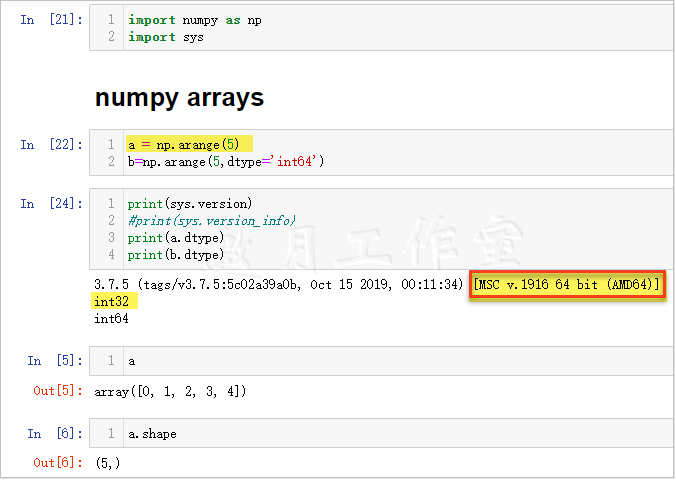
注意：虽然windows操作系统，JDK，python都是64位，但是Numpy默认建立的int类型即是32位。这与原书中作者的描述不同，如果你需要64位，可以通过上面的示例修改默认值。以上示例可能对很多场景下的Numpy数据类型与python数据类型不一致时特别有用。
如你所见，该向量有5个元素，它们的值分别是从0~4。该数组的shape属性是一个元组，就本例而言，这是一个单元素元组，存放的是数组在每一个维度的长度。
2.2创建多维数组
1 m = np.array([np.arange(2), np.arange(2)]) 2 print(m) 3 print(m.shape) 4 # [[0 1] 5 # [0 1]] 6 # (2, 2)
以上用arange()子例程直接建立了一个2×2的数组，而利用array()函数创建数组时，则需要传递给它一个对象，同时这个对象还必须是数组类型的，如Python的列表。在上面的例子中，我们传给它的是由两个数组组成的一个列表。该对象是array()函数唯一所需的参数，而NumPy的函数往往有多个可选参数，而且这些参数都带有预定义的缺省选项。
2.3选择NumPy数组元素
1 a = np.array([[1,2],[3,4]])
此时，a[0,0]=1,...a[1,1]=4
2.4.1 数据类型对象
数据类型对象是numpy.dtype类的实例。再强调一次，数组也有数据类型。严格地讲，NumPy数组中的每个元素都要具有相同的数据类型。数据类型对象表明了数据占用的字节数。所占用字节的具体数目一般存放在类dtype的itemsize属性中。
1 print(a.dtype.itemsize) 2 # 4
64位对应的是8
2.4.2 字符码
NumPy之所以提供字符码，是为了与其前身Numeric向后兼容。一般我们不建议使用字符码，这里为什么又提供这些代码呢？因为我们会在许多地方碰到它们，但是，编写代码时我们应当使用dtype对象。下表展示了常见的一些数据类型及其相应的字符码。
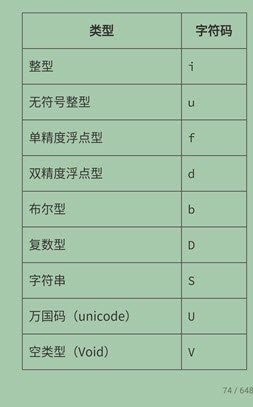
1 1 np.arange(7, dtype='f') #生成一个单精度浮点型的数组。 2 2 np.arange(7, dtype='D')#生成一个复数类型的数组。注意复数转化为int会报错
/* array([0., 1., 2., 3., 4., 5., 6.], dtype=float32) array([0.+0.j, 1.+0.j, 2.+0.j, 3.+0.j, 4.+0.j, 5.+0.j, 6.+0.j]) */
2.4.3 dtype构造函数
1 print(np.sctypeDict.keys())
/*
dict_keys(['?', 0, 'byte', 'b', 1, 'ubyte', 'B', 2, 'short', 'h', 3, 'ushort', 'H', 4, 'i', 5, 'uint', 'I', 6, 'intp', 'p', 9, 'uintp', 'P', 10,
'long', 'l', 7, 'L', 8, 'longlong', 'q', 'ulonglong', 'Q', 'half', 'e', 23, 'f', 11, 'double', 'd', 12, 'longdouble', 'g', 13, 'cfloat', 'F', 14,
'cdouble', 'D', 15, 'clongdouble', 'G', 16, 'O', 17, 'S', 18, 'unicode', 'U', 19, 'void', 'V', 20, 'M', 21, 'm', 22, 'bool8', 'Bool', 'b1',
'int64', 'Int64', 'i8', 'uint64', 'Uint64', 'u8', 'float16', 'Float16', 'f2', 'float32', 'Float32', 'f4', 'float64', 'Float64', 'f8',
'complex64', 'Complex32', 'c8', 'complex128', 'Complex64', 'c16', 'object0', 'Object0', 'bytes0', 'Bytes0', 'str0', 'Str0', 'void0',
'Void0', 'datetime64', 'Datetime64', 'M8', 'timedelta64', 'Timedelta64', 'm8', 'int32', 'Int32', 'i4', 'uint32', 'UInt32', 'u4', 'UInt64',
'int16', 'Int16', 'i2', 'uint16', 'UInt16', 'u2', 'int8', 'Int8', 'i1', 'uint8', 'UInt8', 'u1', 'complex_', 'int0', 'uint0', 'single',
'csingle', 'singlecomplex', 'float_', 'intc', 'uintc', 'int_', 'longfloat', 'clongfloat', 'longcomplex', 'bool_', 'bytes_', 'string_',
'unicode_', 'object_', 'str_', 'int', 'float', 'complex', 'bool', 'object', 'str', 'bytes', 'a'])
*/
2.5一维数组的切片与索引
一维NumPy数组的切片操作与Python列表的切片一样。下面先来定义包含数字0、1、2, …, 8的一个数组，然后通过指定下标3～7来选择该数组的部分元素，这实际上就是提取数组中值为3～6的那些元素。
1 a = np.arange(9) 2 a[3:7]
Out:
array([3, 4, 5, 6])
我们可以用下标选择元素，下标范围从0～7，而且下标每次递增2，如下所示。
a[:7:2]
Out:
array([0, 2, 4, 6])
正如使用Python那样，我们也可用负值下标来反转数组。
a[::-1]
Out:
[8, 7, 6, 5, 4, 3, 2, 1, 0]
2.6处理数组形状
前面我们学习过reshape()函数，实际上，除了数组形状的调整外，数组的扩充也是一个经常碰到的乏味工作。比如，我们可以想象一下将多维数组转换成一维数组时的情形。我们创建一个数组b，下面的多个例子都会用到它。
1 b = np.arange(24).reshape(2,3,4) 2 print(b)
Out:
[[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]],这个过程可以理解为先2，再3，后4，最后得到一个2×3×4的数组
我们可以利用以下函数处理数组的形状。
拆解：可以用ravel()函数将多维数组变成一维数组，代码如下。
1 print(b.ravel())
Out:
[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
拉直（Flatten）：flatten()函数的名字取得非常贴切，其功能与ravel()相同。可是，flatten()返回的是真实的数组，需要分配新的内存空间；而ravel()函数返回的只是数组的视图。这意味着，我们可以像下面这样直接操作数组。
1 print(b.flatten())
Out:
[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]
用元组指定数组形状：除reshape()函数外，还可以用元组来轻松定义数组的形状，代码如下。
1 b.shape = (6,4) 2 print(b)
Out:
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]
可见，上述代码直接改变了数组的形状。这样，我们就得到了一个6×4的数组。
转置：在线性代数中，矩阵的转置操作非常常见。转置是一种数据变换方法，对于二维表而言，转置就意味着行变成列，同时列变成行。转置也可以通过下列代码完成。
1 print(b.transpose())
Out:
[[ 0, 4, 8, 12, 16, 20],
[ 1, 5, 9, 13, 17, 21],
[ 2, 6, 10, 14, 18, 22],
[ 3, 7, 11, 15, 19, 23]]
调整大小：函数resize()的作用类似于reshape()，但是会改变所作用的数组。
1 b.resize((2,12))
Out:
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]]
2.6.1 堆叠数组
从深度看，数组既可以横向叠放，也可以竖向叠放。为此，可以使用vstack()、dstack()、hstack()、column_stack()、row_stack()和concatenate()等函数。在此之前，我们先要建立某些数组。
1 a = np.arange(9).reshape(3,3) 2 print(a)
Out:
[[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
1 b = 2 * a 2 print(b)
Out:
[[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]]
就像前面所说的，可以用下列技术来堆放数组。
水平叠加：先介绍水平叠加方式，即用元组确定ndarrays数组的形状，然后交给hstack()函数来码放这些数组，具体如下。
np.hstack((a, b))
Out:
[[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8, 10],
[ 6, 7, 8, 12, 14, 16]]
用concatenate()函数也能达到同样的效果，代码如下。
np.concatenate((a, b), axis=1)
Out:
[[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8, 10],
[ 6, 7, 8, 12, 14, 16]]
水平叠加过程的示意图如图2-2所示。
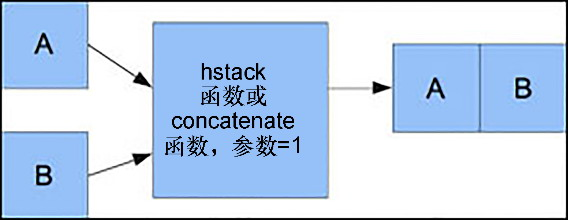
垂直叠加：使用垂直叠加方法时，先要构建一个元组，然后将元组交给vstack()函数来码放数组，代码如下。
np.vstack((a, b))
Out:
[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]]
当参数axis设置为0时，concatenate()函数也会得到同样的效果。实际上，这是该参数的缺省值，代码如下。
np.concatenate((a, b), axis=0)
Out:
[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]]
垂直叠加过程的示意图如图2-3所示。
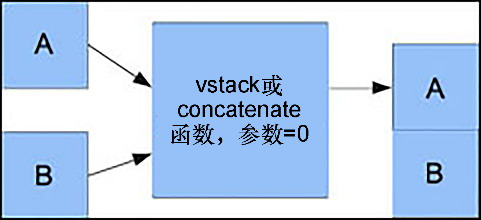
深度叠加：除此之外，还有一种深度叠加方法，这要用到dstack()函数和一个元组。这种方法是沿着第三个坐标轴（纵向）的方向来叠加一摞数组。举例来说，我们可以在一个图像数据的二维数组上叠加另一幅图像的数据，代码如下。
np.dstack((a, b))
Out:
Array([[[ 0, 0],
[ 1, 2],
[ 2, 4]],
[[ 3, 6],
[ 4, 8],
[ 5, 10]],
[[ 6, 12],
[ 7, 14],
[ 8, 16]]])
列式堆叠：column_stack()函数以列方式对一维数组进行堆叠，代码如下。
oned = np.arange(2) print(oned)
Out: [0, 1]
twice_oned = 2 * oned print(twice_oned)
Out: [0, 2]
np.column_stack((oned, twice_oned))
Out:
Array([[0, 0],
[1, 2]])
用这种方法堆叠二维数组时，过程类似于hstack()函数，代码如下。
np.column_stack((a, b))
Out:
[[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8, 10],
[ 6, 7, 8, 12, 14, 16]]
np.column_stack((a, b)) == np.hstack((a, b))
Out:
Array([[ True, True, True, True, True, True],
[ True, True, True, True, True, True],
[ True, True, True, True, True, True]],
Dtype=bool)
是的，你猜得没错！我们用“==”运算符对两个数组进行了比对。
行式堆叠：同时，NumPy自然也有以行方式对数组进行堆叠的函数，这个用于一维数组的函数名为row_stack()，它将数组作为行码放到二维数组中，代码如下。
np.row_stack((oned, twice_oned))
Out:
[[0, 1],
[0, 2]]
对于二维数组，row_stack()函数相当于vstack()函数，代码如下。
np.row_stack((a, b))
Out:
Array([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 0, 2, 4],
[ 6, 8, 10],
[12, 14, 16]])
np.row_stack((a,b)) == np.vstack((a, b))
Out:
Array([[ True, True, True],
[ True, True, True],
[ True, True, True],
[ True, True, True],
[ True, True, True],
[ True, True, True]], dtype=bool)
2.6.2 拆分NumPy数组
我可以从纵向、横向和深度方向来拆分数组，相关函数有hsplit()、vsplit()、dsplit()和split()。我们既可以把数组分成相同形状的数组，也可以从规定的位置开始切取数组。下面对相关函数逐个详解。
横向拆分：对于一个3×3数组，可以沿着横轴方向将其分解为3部分，并且各部分的大小和形状完全一致，代码（它取自本书代码包中的splitting.py文件）如下。
a = np.arange(9).reshape(3,3) print(a)
Out:
[[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
np.hsplit(a, 3)
Out:
[array([[0],
[3],
[6]]),
Array([[1],
[4],
[7]]),
Array([[2],
[5],
[8]])]
这相当于调用了参数axis=1的split()函数。
np.split(a, 3, axis=1) #print(a)
Out:
[array([[0],
[3],
[6]]),
Array([[1],
[4],
[7]]),
Array([[2],
[5],
[8]])]
纵向拆分：vsplit()函数将沿着纵轴方向分解数组。
np.vsplit(a, 3)
Out: [array([[0, 1, 2]]), array([[3, 4, 5]]),
Array([[6, 7, 8]])]
当参数axis=0时，split()函数也会沿着纵轴方向分解数组，代码如下
np.split(a, 3, axis=0)
Out: [array([[0, 1, 2]]), array([[3, 4, 5]]),
Array([[6, 7, 8]])]
深向拆分：dsplit()函数会沿着深度方向分解数组。下面以秩为3的数组为例进行说明。
c = np.arange(27).reshape(3, 3, 3) print(c)
Out:
[[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]]
np.dsplit(c, 3)
Out:
[array([[[ 0],
[ 3],
[ 6]],
[[ 9],
[12],
[15]],
[[18],
[21],
[24]]]),
Array([[[ 1],
[ 4],
[ 7]],
[[10],
[13],
[16]],
[[19],
[22],
[25]]]),
Array([[[ 2],
[ 5],
[ 8]],
[[11],
[14],
[17]],
[[20],
[23],
[26]]])]
2.6.3 NumPy数组的属性
下面举例说明NumPy数组各种属性的详细用法。我们创建一个数组b，以便后面的例子使用。
b = np.arange(24).reshape(2, 12) print(b)
Out:
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]]
除shape和dtype属性外，ndarray类型的属性还很多，下面逐一列出。
Ndim属性存储的是维度的数量，下面举例说明。
print(b.ndim)
Out: 2
Size属性用来保存元素的数量，用法如下。
print(b.size)
Out: 24
Itemsize属性可以返回数组中各个元素所占用的字节数，代码如下。
print(b.itemsize)
Out: 8
如果想知道存储整个数组所需的字节数量，可以求助于nbytes属性。这个属性的值正好是itemsize属性值和size属性值之积。
print( b.nbytes)
Out: 192
print(b.size * b.itemsize)
Out: 192
T属性的作用与transpose()函数相同，下面举例说明。
print(b=b.resize(6,4))
Out:
Array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
print(b.T)
Out:
[[ 0, 4, 8, 12, 16, 20],
[ 1, 5, 9, 13, 17, 21],
[ 2, 6, 10, 14, 18, 22],
[ 3, 7, 11, 15, 19, 23]]
如果数组的秩（rank）小于2，那么所得只是一个数组的视图。
b.ndim
Out: 1
b.T
Out: array([0, 1, 2, 3, 4])
对于NumPy来说，复数用j表示，下面举例说明如何用复数生成一个数组。
b = np.array([1.j + 1, 2.j + 3]) print(b)
Out: [ 1.+1.j, 3.+2.j]
Real属性将返回数组的实部；当数组元素全为实数时，就返回数组本身，代码如下。
print(b.real)
Out: [ 1., 3.]
Imag属性存放的是数组的虚部。
print(b.imag)
Out: [ 1., 2.]
如果数组含有复数，那么它的数据类型将自动变为复数类型，代码如下。
print(b.dtype)
Out: dtype(‘complex128’)
print(b.dtype.str)
Out: ‘<c16’
Flat属性可返回一个numpy.flatiter对象，这是获得flatiter对象的唯一方法，但我们无法访问flatiter的构造函数。我们可以使用flat的迭代器来遍历数组，就像遍历“胖”数组那样，代码如下。
b = np.arange(4).reshape(2,2) print(b)
Out:
Array([[0, 1],
[2, 3]])
f = b.flat print(f)
Out: <numpy.flatiter object at 0x103013e00>
for item in f: print(item)
Out:
0
1
2
3
当然，取得flatiter对象的元素也不难，代码如下。
print(b.flat[2])
Out: 2
此外，还可以请求多个元素，代码如下。
print(b.flat[[1,3]])
Out: array([1, 3])
同时，还可以给flat属性赋值。不过，需要注意的是，这个值将会覆盖整个数组内所有元素的值，下面举例说明。
b.flat = 7
print(b)
Out:
[[7, 7],
[7, 7]]
此外，还可以返回指定的元素，代码如下。
b.flat[[1,3]] = 1
print(b)
Out:
[[7, 1],
[7, 1]]
图2-4是对ndarray各种属性的一个小结。
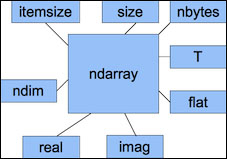
2.6.4 数组的转换
我们可以把NumPy数组转换成Python列表，使用tolist()函数即可。下面简单解释一下。
转换成列表：
b = np.array([1.j + 1, 2.j + 3]) print(b)
Out: [ 1.+1.j, 3.+2.j]
b.tolist()
Out: [(1+1j), (3+2j)]
Astype()函数可以把数组元素转换成指定类型，代码如下。
b = np.array([1.j + 1, 2.j + 3]) print(b)
Out: array([ 1.+1.j, 3.+2.j])
b.astype(int)
/* d:\tools\python37\lib\site-packages\ipykernel_launcher.py:1: ComplexWarning: Casting complex values to real discards the imaginary part """Entry point for launching an IPython kernel. */
b.astype(‘complex’)
Out: [ 1.+1.j, 3.+2.j]
提示:当complex类型转换成int类型时，虚部将被丢弃。另外，我们还需要将数据类型的名称以字符串的形式传递给astype()函数。
上述代码没有显示警告信息，因为这次使用的是正确的数据类型。
2.7创建数组的视图和拷贝
在介绍ravel()函数的示例中，我们提到了视图的概念。不过，请不要与数据库中的视图概念混淆。在NumPy的世界里，视图不是只读的，因为你不可能守着基础数据一动不动。关键在于要知道当前处理的是共享的数组视图还是数组数据的副本。举例来说，我们可以取数组的一部分来生成视图。这意味着，如果先将数组的某部分赋给一个变量，然后修改原数组中相应位置的数据，那么这个变量的值也会随之变化。我们可以根据SciPy包中的面部照片来创建数组，然后创建视图，随后修改它。这里，莱娜肖像的数组是从SciPy函数获得的。
（1） 获取面部图片。
1 Face = scipy.misc.face()
（2） 为该面部数组创建副本。
1 Acopy = face.copy()
（3）为该数组创建一个视图。
1 Aview = face.view()
（4） 通过flat迭代器将视图中所有的值全部设为0。
1 Aview.flat = 0
最后，只有一幅图片可以看到图像，而其他图片根本看不到什么，如图2-5所示。
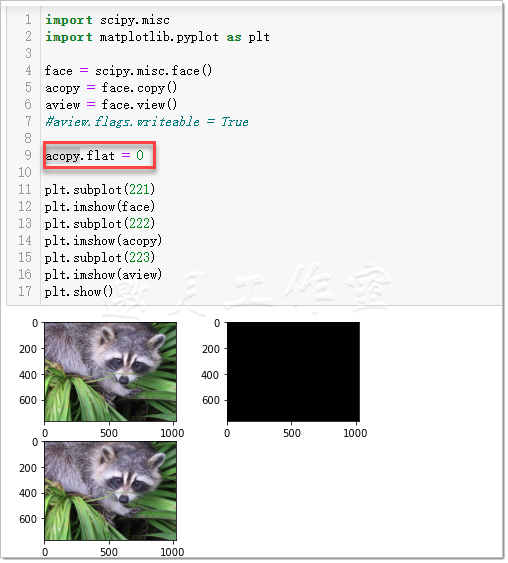
下面的代码很好地展示了数组的视图和副本的特点。
Import scipy.misc Import matplotlib.pyplot as plt Face = scipy.misc.face() Acopy = face.copy() Aview = face.view() #Aview.flags.writeable = True ####执行报错：ValueError: cannot set WRITEABLE flag to True of this array Aview.flat = 0 ####ValueError: array is read-only Plt.subplot(221) Plt.imshow(face) Plt.subplot(222) Plt.imshow(acopy) Plt.subplot(223) Plt.imshow(aview) Plt.show()
可见，在程序结束部分修改视图，同时改变了原来的莱娜数组。这导致3副图片全部变蓝（如果阅读的是本书的印刷版，也可能显示为黑色），复制的数组则没有任何变化。所以一定要记住：视图不是只读的。
邀月注：原书结论恰恰相反。
2.8花式索引
花式索引是一种传统的索引方法，它不使用整数或者切片。这里，我们将利用花式索引把莱娜照片对角线上的值全部设置为0，相当于沿着两条交叉的对角线画两条黑线。
下面我们给出本例中的相应代码。
Import scipy.misc Import matplotlib.pyplot as plt Face = scipy.misc.face() Xmax = face.shape[0] Ymax = face.shape[1] Face=face[:min(xmax,ymax),:min(xmax,ymax)] Xmax = face.shape[0] Ymax = face.shape[1] #Face[range(xmax), range(ymax)] = 0#ValueError: assignment destination is read-only #Face[range(xmax-1,-1,-1), range(ymax)] = 0 #ValueError: assignment destination is read-only Plt.imshow(face) Plt.show()
下面我们对上述代码进行简单说明。
（1）将第一条对角线上的值设为0。
（2 ）为了将对角线上的值设置为0，我们需要给x和y值（直角坐标系中的坐标）规定两个不同的范围。
1 Face[range(xmax), range(ymax)] = 0
（3）将另一条对角线上的值设为0。
（4）要设置另一条对角线上的值，需要规定两个不同的取值范围，但是规则不变。
1 Face[range(xmax-1,-1,-1), range(ymax)] = 0
划掉相片对角线后，最后得到图2-6所示的效果。
运行报错
我们给x和y规定了不同的取值范围，这些范围用来索引莱娜数组。花式索引是在一个内部的NumPy迭代器对象的基础上实现的，分3步完成。
（1）创建迭代器对象。
（2）将迭代器对象绑定到数组。
（3）经由迭代器访问数组元素，利用位置列表进行索引。
2.9基于位置列表的索引方法
1 import scipy.misc 2 import matplotlib.pyplot as plt 3 import numpy as np 4 5 face = scipy.misc.face() 6 xmax = face.shape[0] 7 ymax = face.shape[1] 8 9 def shuffle_indices(size): 10 arr = np.arange(size) 11 np.random.shuffle(arr) 12 13 return arr 14 15 xindices = shuffle_indices(xmax) 16 np.testing.assert_equal(len(xindices), xmax) 17 yindices = shuffle_indices(ymax) 18 np.testing.assert_equal(len(yindices), ymax) 19 plt.imshow(face[np.ix_(xindices, yindices)]) 20 plt.show()
下面利用ix_()函数将莱娜照片中的像素完全打乱。注意，本例中的代码没有提供注释。完整的代码请参考本书代码包中的ix.py文件。
这个函数可以根据多个序列生成一个网格，它需要一个一维序列作为参数并返回一个由NumPy数组构成的元组。
In : ix_([0,1], [2,3])
Out:(array([[0],[1]]), array([[2, 3]]))
利用位置列表索引NumPy数组的过程如下。
（1）打乱数组的索引。
（2）我们用numpy.random子程序包中的shuffle()函数把数组中的元素按随机的索引号重新排列，使得数组产生相应的变化。
1 Def shuffle_indices(size): 2 Arr = np.arange(size) 3 Np.random.shuffle(arr) 4 Return arr
（3）使用下面的代码画出打乱后的索引。
1 Plt.imshow( face[np.ix_(xindices, yindices)])
（4）莱娜照片的像素被完全打乱后，变成图2-7所示的样子。
2.10用布尔型变量索引NumPy数组
布尔型索引是指根据布尔型数组来索引元素的方法，属于花式索引系列。因为布尔型索引是花式索引的一个分类，所以它们的使用方法基本相同。
下面用代码（详见本书代码包中的boolean_indexing.py文件）具体演示其使用方法。
1 import scipy.misc 2 import matplotlib.pyplot as plt 3 import numpy as np 4 5 face = scipy.misc.face() 6 xmax = face.shape[0] 7 ymax = face.shape[1] 8 face=face[:min(xmax,ymax),:min(xmax,ymax)] 9 10 def get_indices(size): 11 arr = np.arange(size) 12 return arr % 4 == 0 13 14 face1 = face.copy() 15 xindices = get_indices(face.shape[0]) 16 yindices = get_indices(face.shape[1]) 17 face1[xindices, yindices] = 0 18 plt.subplot(211) 19 plt.imshow(face1) 20 face2 = face.copy() 21 face2[(face > face.max()/4) & (face < 3 * face.max()/4)] = 0 22 plt.subplot(212) 23 plt.imshow(face2) 24 plt.show()
上述代码利用一种特殊的迭代器对象来索引元素，下面进行简单说明。
（1）在对角线上画点。
（2）这类似于花式索引，不过这里选择的是照片对角线上可以被4整除的那些位置上的点。
1 Def get_indices(size): 2 Arr = np.arange(size) 3 Return arr % 4 == 0 4 5 #然后我们仅绘出选定的那些点。 6 Face1 = face.copy() 7 Xindices = get_indices(face.shape[0]) 8 Yindices = get_indices(face.shape[1]) 9 Face1[xindices, yindices] = 0 10 Plt.subplot(211) 11 Plt.imshow(face1)
（3 根据元素值的情况置零。
（4）选取数组值介于最大值的1/4～3/4的那些元素，将其设置为0。
1 Face2[(face > face.max()/4) & (face < 3 * face.max()/4)] = 0
（5）两幅新照片如图2-8所示。
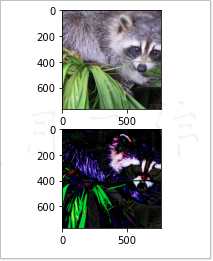
2.11NumPy数组的广播
当操作对象的形状不一样时，NumPy会尽力进行处理。
例如，假设一个数组要跟一个标量相乘，这时标量需要根据数组的形状进行扩展，然后才可以执行乘法运算。这个扩展的过程叫作广播（broadcasting）。下面用代码加以说明。
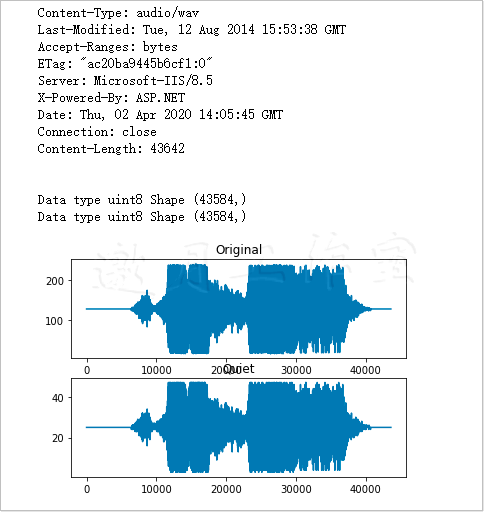
1 import scipy.io.wavfile as sw 2 import matplotlib.pyplot as plt 3 import urllib 4 import numpy as np 5 6 request = urllib.request.Request('http://www.thesoundarchive.com/austinpowers/smashingbaby.wav') 7 response = urllib.request.urlopen(request) 8 print(response.info()) 9 WAV_FILE = 'smashingbaby.wav' 10 filehandle = open(WAV_FILE, 'wb') 11 filehandle.write(response.read()) 12 filehandle.close() 13 sample_rate, data = sw.read(WAV_FILE) 14 print("Data type", data.dtype, "Shape", data.shape) 15 16 plt.subplot(2, 1, 1) 17 plt.title("Original") 18 plt.plot(data) 19 20 newdata = data * 0.2 21 newdata = newdata.astype(np.uint8) 22 print("Data type", newdata.dtype, "Shape", newdata.shape) 23 24 sw.write("quiet.wav", 25 sample_rate, newdata) 26 27 plt.subplot(2, 1, 2) 28 plt.title("Quiet") 29 plt.plot(newdata) 30 31 plt.show()
下面，我们将下载一个音频文件，然后以此为基础，生成一个新的静音版本。
（1）读取WAV文件。
我们将使用标准的Python代码来下载电影《王牌大贱谍》（Austin Powers）中的狂嚎式歌曲《Smashing, baby》的声音文件。SciPy中有一个wavfile子程序包，可以用来加载音频数据，或者生成WAV格式的文件。如果此前已经安装了SciPy，那么现在就可以直接使用这个子程序包了。我们可以使用函数read()读取文件，它返回一个数据阵列及采样率，不过，这里只对数据本身感兴趣。
Sample_rate, data = scipy.io.wavfile.read(WAV_FILE)
（2）绘制原WAV数据。
这里，我们利用matplotlib绘制原始WAV数据并用一个子图来显示标题“Original”，代码如下。
Plt.subplot(2, 1, 1)
Plt.title(“Original”)
Plt.plot(data)
（3）新建一个数组。
现在，我们要用NumPy来生成一段“寂静的”声音。实际上就是将原数组的值乘以一个常数，从而得到一个新数组，因为这个新数组的元素值肯定是变小了。这正是广播技术的用武之地。最后，我们要确保新数组与原数组的类型一致，即WAV格式。
Newdata = data * 0.2
Newdata = newdata.astype(np.uint8)
（4）写入一个WAV文件中。
我们将新数组保存到一个新的WAV文件中，代码如下。
Scipy.io.wavfile.write(“quiet.wav”,
Sample_rate, newdata)
（5）绘制出新的WAV数据。
我们可以使用matplotlib来画出新数组中的数据，如下所示。
1 Plt.subplot(2, 1, 2) 2 Plt.title(“Quiet”) 3 Plt.plot(newdata) 4 Plt.show()
图2-9展示了原始的WAV文件中的数据的图像以及数值变小后新数组的图像。
2.12小结
本章，我们学习了NumPy的基础知识：数据类型和数组。数组具有许多属性，这些属性都是用来描述该数组的特性的。我们探讨的属性之一便是数据类型，实际上，NumPy是通过一个成熟完备的对象来表示这个属性的。
与Python标准的列表相比，NumPy数组使用的切片和索引方法更加高效。此外，NumPy数组还能够对多维度数组进行处理。
我们可以用各种方式改变数组的形状，如堆叠、重定尺寸、重塑形状以及拆分等。在本章中，我们还为处理数组的形状介绍了许多简便易用的函数。
有了这些基础知识后，从第4章开始，我们就要学习如何通过常见的函数来分析数据了，这将涉及主要统计函数和数值函数的用法。
我们鼓励读者阅读“参考文献”部分中提到的书籍，以拓展大家在NumPy库知识方面的深度和广度。
第2章完。
随书源码官方下载：
https://www.ptpress.com.cn/shopping/buy?bookId=bae24ecb-a1a1-41c7-be7c-d913b163c111
需要登录后免费下载。
