周练（6）5. 最长回文子串

动态规划

/*
* @lc app=leetcode.cn id=5 lang=cpp
*
* [5] 最长回文子串
*/

#include <iostream>
#include <string>
#include <cstdlib>
#include <cstdio>
using namespace std;

// @lc code=start
class Solution {
public:
    //暴力解法：超时
	// string longestPalindrome(string s)
	// {
	// 	int maxLen = 1;
    //     int begin = 0;
    //     int slen = s.length();
	// 	for (int i = 0; i < slen - 1; ++i)
	// 	{
	// 		for (int j = i + 1; j < slen; ++j)
	// 		{
	// 			if (j - i + 1 > maxLen && validPalindromic(s, i, j))
	// 			{
    //                 maxLen = j - i + 1;
    //                 begin = i;
	// 			}
	// 		}
	// 	}
	// 	return s.substr(begin, maxLen);
	// }

	// bool validPalindromic(string s, int left, int right)
	// {
    //     while (left < right)
    //     {
    //         if (s[left] != s[right])
    //         {
    //             return false;
    //         }
    //         left++;
    //         right--;
    //     }
    //     return true;        
	// }

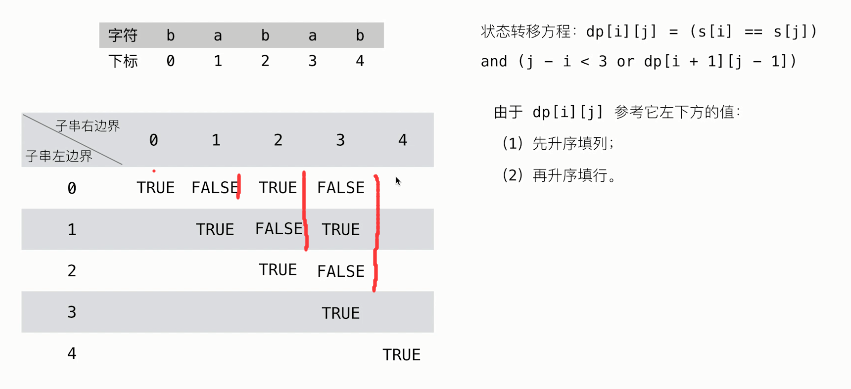
    //动态规划:一个回文去掉两头，仍然是回文
    //状态: dp[i][j] 表示子串s[i..j]是否是回文子串
    //得到状态转移方程: dp[i][j] = (s[i] == s[j]) and dp[i+1][j-1]
    // 边界条件: j - 1 - (i + 1) + 1 < 2，整理得 j - i < 3
    // 初始化dp[i][j] = true
    // 输出．在得到一个状态的值为true的时候，记录起始位置和长0填表完成以后再截取
    string longestPalindrome(string s)
    {
        int slen = s.length();
        if (slen < 2) 
        {
            return s;            
        }
        int maxLen = 1;
        int begin = 0;

        //dp[i][j] 表示 s[i..j] 是否是回文串 [i, j]
        int dp[slen][slen];
        for (int i = 0; i < slen; i++)
        {
            dp[i][i] = true;
        }

        // 注意：左下角先填
        for (int j = 1; j < slen; j++)
        {
            for (int i = 0; i < j; i++)
            {
                if (s[i] != s[j])           // 先写列
                {
                    dp[i][j] = false;
                }
                else 
                {
                    if (j - i < 3)         // 长度<=2，没必要再判断
                    {
                        dp[i][j] = true;
                    }
                    else 
                    {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][j] == true 成立, 就表示子串 s[i..j] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen)
                {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substr(begin, maxLen);
    }
};

// @lc code=end

python版本

#
# @lc app=leetcode.cn id=5 lang=python3
#
# [5] 最长回文子串
#

# @lc code=start
class Solution:
    def longestPalindrome(self, s: str) -> str:
        slen = len(s)
        if slen < 2:
            return s 
        
        maxLen = 1
        begin = 0
        dp = [[True] * slen for _ in range(slen)]

        for j in range(slen):
            for i in range(0, j):
                if s[i] != s[j]:
                    dp[i][j] = False
                else:
                    if j - i < 3:
                        dp[i][j] = True
                    else:
                        dp[i][j] = dp[i + 1][j - 1]

                if dp[i][j] and j - i + 1 > maxLen:
                    maxLen = j - i + 1
                    begin = i
            
        return s[begin:begin+maxLen]


# @lc code=end

Manacher算法