【邱希鹏】nndl-chap3-逻辑回归&softmax

1. 逻辑回归解决二分类问题

1.1 生成数据集

• '+' 从高斯分布采样 (X, Y) ~ N(3, 6, 1, 1, 0).
  

• 'o' 从高斯分布采样 (X, Y) ~ N(6, 3, 1, 1, 0)
  

import tensorflow as tf
import matplotlib.pyplot as plt

from matplotlib import animation, rc
from IPython.display import HTML
import matplotlib.cm as cm
import numpy as np
%matplotlib inline

dot_num = 100
x_p = np.random.normal(3., 1, dot_num)
y_p = np.random.normal(6., 1, dot_num)
y = np.ones(dot_num)
C1 = np.array([x_p, y_p, y]).T

x_n = np.random.normal(6., 1, dot_num)
y_n = np.random.normal(3., 1, dot_num)
y = np.zeros(dot_num)
C2 = np.array([x_n, y_n, y]).T

plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')

data_set = np.concatenate((C1, C2), axis=0)
np.random.shuffle(data_set)

1.2 建立模型

• 逻辑函数的交叉熵损失函数：

\[L = -\sum _{i=1}^{n}y_ilog(p_i)+(1-y_i)log(1-p_i) \]

• \(y_i\) 指 i 的真实值，\(p_i\) 指 i 的预测值。

• 下面loss函数中在预测值pred后面加上了epsilon。

epsilon = 1e-12
class LogisticRegression():
    def __init__(self):
        self.W = tf.Variable(shape=[2, 1], dtype=tf.float32,
            initial_value=tf.random.uniform(shape=[2, 1], minval=-0.1, maxval=0.1))
        self.b = tf.Variable(shape=[1], dtype=tf.float32, initial_value=tf.zeros(shape=[1]))

        self.trainable_variables = [self.W, self.b]

    @tf.function
    def __call__(self, inp):
        logits = tf.matmul(inp, self.W) + self.b         #shape(N, 1)
        pred = tf.nn.sigmoid(logits)
        return pred

@tf.function
def compute_loss(pred, label):
    if not isinstance(label, tf.Tensor):
        label = tf.constant(label, dtype=tf.float32)
    pred = tf.squeeze(pred, axis=1)

    '''============================='''
    #输入label shape(N,), pred shape(N,)
    #输出 losses shape(N,) 每一个样本一个loss
    #todo 填空一，实现sigmoid的交叉熵损失函数(不使用tf内置的loss 函数)

    #losses = -label*tf.math.log(pred) - (1-label)* tf.math.log(1-pred)
    losses = -label*tf.math.log(pred+epsilon) - (1.-label)* tf.math.log(1.-pred+epsilon)
     '''============================='''

    loss = tf.reduce_mean(losses)

    pred = tf.where(pred>0.5, tf.ones_like(pred), tf.zeros_like(pred))            #大于0.5预测正确，否则预测错误，形成判定矩阵
    accuracy = tf.reduce_mean(tf.cast(tf.equal(label, pred), dtype=tf.float32))   #计算正确率
    return loss, accuracy


@tf.function
def train_one_step(model, optimizer, x, y):
    with tf.GradientTape() as tape:
        pred = model(x)
        loss, accuracy = compute_loss(pred, y)

    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(grads, model.trainable_variables))
    return loss, accuracy, model.W, model.b

1.3 实例化一个模型，进行训练

if __name__ == '__main__':
    model = LogisticRegression()
    opt = tf.keras.optimizers.SGD(learning_rate=0.01)              #SGD优化器
    x1, x2, y = list(zip(*data_set))
    x = list(zip(x1, x2))
    animation_fram = []

    for i in range(200):
        loss, accuracy, W_opt, b_opt = train_one_step(model, opt, x, y)
        animation_fram.append((W_opt.numpy()[0, 0], W_opt.numpy()[1, 0], b_opt.numpy(), loss.numpy()))
        if i%20 == 0:
            print(f'loss: {loss.numpy():.4}\t accuracy: {accuracy.numpy():.4}')

loss: 0.7929	 accuracy: 0.08
loss: 0.5811	 accuracy: 0.995
loss: 0.4555	 accuracy: 0.995
loss: 0.3761	 accuracy: 0.995
loss: 0.3223	 accuracy: 0.995
loss: 0.2837	 accuracy: 0.995
loss: 0.2547	 accuracy: 0.995
loss: 0.232	 accuracy: 0.995
loss: 0.2139	 accuracy: 0.995
loss: 0.199	 accuracy: 0.995

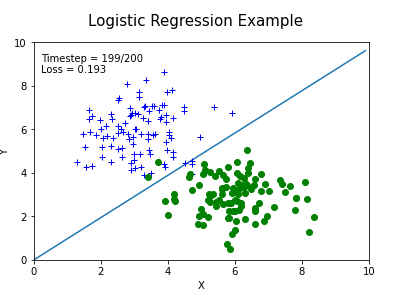
1.4 展示动态结果

f, ax = plt.subplots(figsize=(6,4))                             #f是图像对象，ax是坐标轴对象
f.suptitle('Logistic Regression Example', fontsize=15)
plt.ylabel('Y')
plt.xlabel('X')
ax.set_xlim(0, 10)
ax.set_ylim(0, 10)

line_d, = ax.plot([], [], label='fit_line')
C1_dots, = ax.plot([], [], '+', c='b', label='actual_dots')
C2_dots, = ax.plot([], [], 'o', c='g' ,label='actual_dots')


frame_text = ax.text(0.02, 0.95,'',horizontalalignment='left',verticalalignment='top', transform=ax.transAxes)

def init():
    line_d.set_data([],[])
    C1_dots.set_data([],[])
    C2_dots.set_data([],[])
    return (line_d,) + (C1_dots,) + (C2_dots,)

def animate(i):
    xx = np.arange(10, step=0.1)
    a = animation_fram[i][0]
    b = animation_fram[i][1]
    c = animation_fram[i][2]
    yy = a/-b * xx +c/-b
    line_d.set_data(xx, yy)

    C1_dots.set_data(C1[:, 0], C1[:, 1])
    C2_dots.set_data(C2[:, 0], C2[:, 1])

    frame_text.set_text('Timestep = %.1d/%.1d\nLoss = %.3f' % (i, len(animation_fram), animation_fram[i][3]))

    return (line_d,) + (C1_dots,) + (C2_dots,)


#FuncAnimation函数绘制动图，f是画布，animate是自定义动画函数，init_func自定义开始帧，即传入init初始化函数，
#frames动画长度，一次循环包含的帧数，在函数运行时，其值会传递给函数animate(i)的形参“i”，interval更新频率，以ms计，blit选择更新所有点，还是仅更新产生变化的点。
anim = animation.FuncAnimation(f, animate, init_func=init, frames=len(animation_fram), interval=30, blit=True)
HTML(anim.to_html5_video())

动态截图：

最终结果：

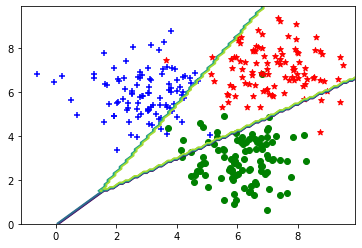
2. softmax回归解决多分类问题

2.1 生成数据集

• '+' 从高斯分布采样 (X, Y) ~ N(3, 6, 1, 1, 0).
  

• 'o' 从高斯分布采样 (X, Y) ~ N(6, 3, 1, 1, 0)
  

• '*' 从高斯分布采样 (X, Y) ~ N(7, 7, 1, 1, 0)
  

import tensorflow as tf
import matplotlib.pyplot as plt

from matplotlib import animation, rc
from IPython.display import HTML
import matplotlib.cm as cm
import numpy as np
%matplotlib inline

dot_num = 100
x_p = np.random.normal(3., 1, dot_num)
y_p = np.random.normal(6., 1, dot_num)
y = np.ones(dot_num)
C1 = np.array([x_p, y_p, y]).T

x_n = np.random.normal(6., 1, dot_num)
y_n = np.random.normal(3., 1, dot_num)
y = np.zeros(dot_num)
C2 = np.array([x_n, y_n, y]).T

x_b = np.random.normal(7., 1, dot_num)
y_b = np.random.normal(7., 1, dot_num)
y = np.ones(dot_num)*2
C3 = np.array([x_b, y_b, y]).T

plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')
plt.scatter(C3[:, 0], C3[:, 1], c='r', marker='*')

data_set = np.concatenate((C1, C2, C3), axis=0)
np.random.shuffle(data_set)

2.2 建立模型

• 建立模型类，定义loss函数，定义一步梯度下降过程函数

• 填空一：在__init__构造函数中 建立模型所需的参数

• 填空二：实现softmax的交叉熵损失函数(不使用tf内置的loss 函数)

softmax的交叉熵损失函数：

\[R(W) = -\frac{1}{N}\sum _{n=1}^{N}\sum _{c=1}^{C}y_{c}^{(n)}logp_{c}^{n}=-\frac{1}{N}\sum _{n=1}^{N}(y^{n})^{T}logp^{n} \\ (y 指真实值，p指预测值.) \]

下面loss函数中在预测值pred后面加上了epsilon。

epsilon = 1e-12
class SoftmaxRegression():
    def __init__(self):
        '''============================='''
        #todo 填空一，构建模型所需的参数 self.W, self.b 可以参考logistic-regression-exercise
        '''============================='''
        # 3个输出
        self.W = tf.Variable(shape=[2, 3], dtype=tf.float32,
                            initial_value=tf.random.uniform(shape=[2,3], minval=-0.1, maxval=0.1))
        self.b = tf.Variable(shape=[1, 3], dtype=tf.float32,
                            initial_value=tf.zeros(shape=[1,3]))
        self.trainable_variables = [self.W, self.b]
    @tf.function
    def __call__(self, inp):
        logits = tf.matmul(inp, self.W) + self.b # shape(N, 3)
        pred = tf.nn.softmax(logits)
        return pred    
    
@tf.function
def compute_loss(pred, label):
    label = tf.one_hot(tf.cast(label, dtype=tf.int32), dtype=tf.float32, depth=3)
    '''============================='''
    #输入label shape(N, 3), pred shape(N, 3)
    #输出 losses shape(N,) 每一个样本一个loss
    #todo 填空二，实现softmax的交叉熵损失函数(不使用tf内置的loss 函数)
    losses = -tf.reduce_mean(label*tf.math.log(pred+epsilon))
    '''============================='''
    loss = tf.reduce_mean(losses)
    
    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(label,axis=1), tf.argmax(pred, axis=1)), dtype=tf.float32))
    return loss, accuracy

@tf.function
def train_one_step(model, optimizer, x, y):
    with tf.GradientTape() as tape:
        pred = model(x)
        loss, accuracy = compute_loss(pred, y)
        
    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(grads, model.trainable_variables))
    return loss, accuracy

2.3 实例化一个模型，进行训练

model = SoftmaxRegression()
opt = tf.keras.optimizers.SGD(learning_rate=0.01)
x1, x2, y = list(zip(*data_set))
x = list(zip(x1, x2))
for i in range(1000):
    loss, accuracy = train_one_step(model, opt, x, y)
    if i%50==49:
        print(f'loss: {loss.numpy():.4}\t accuracy: {accuracy.numpy():.4}')

loss: 0.3136	 accuracy: 0.4233
loss: 0.2784	 accuracy: 0.6833
loss: 0.2534	 accuracy: 0.7933
loss: 0.2347	 accuracy: 0.8467
loss: 0.2202	 accuracy: 0.8733
loss: 0.2086	 accuracy: 0.88
loss: 0.1989	 accuracy: 0.8867
loss: 0.1908	 accuracy: 0.8867
loss: 0.1839	 accuracy: 0.8933
loss: 0.1779	 accuracy: 0.9033
loss: 0.1725	 accuracy: 0.9067
loss: 0.1678	 accuracy: 0.9133
loss: 0.1636	 accuracy: 0.9133
loss: 0.1598	 accuracy: 0.9133
loss: 0.1563	 accuracy: 0.9133
loss: 0.1532	 accuracy: 0.9133
loss: 0.1503	 accuracy: 0.9167
loss: 0.1476	 accuracy: 0.9167
loss: 0.1451	 accuracy: 0.92
loss: 0.1428	 accuracy: 0.92

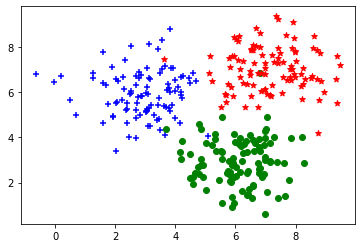
2.4 结果展示

plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')
plt.scatter(C3[:, 0], C3[:, 1], c='r', marker='*')

x = np.arange(0., 10., 0.1)
y = np.arange(0., 10., 0.1)

X, Y = np.meshgrid(x, y)
inp = np.array(list(zip(X.reshape(-1), Y.reshape(-1))), dtype=np.float32)
print(inp.shape)
Z = model(inp)
Z = np.argmax(Z, axis=1)
Z = Z.reshape(X.shape)
plt.contour(X,Y,Z)
plt.show()

(10000, 2)