神经网络梯度下降的推导

https://blog.csdn.net/u012328159/article/details/80081962

https://mp.weixin.qq.com/s?__biz=MzUxMDg4ODg0OQ==&mid=2247484013&idx=1&sn=2f1ec616d9521b801ef318308aa66e57&chksm=f97d5c93ce0ad585343a415be0b346fe18c960a41f45bfe69d0db4128b95b97d76d3c23ed293&mpshare=1&scene=23&srcid=&sharer_sharetime=1591403700835&sharer_shareid=9ed15fc26b568c844598f8638f4c17a4#rd

公式细节推导

Ag课程的总结（单层神经网络）

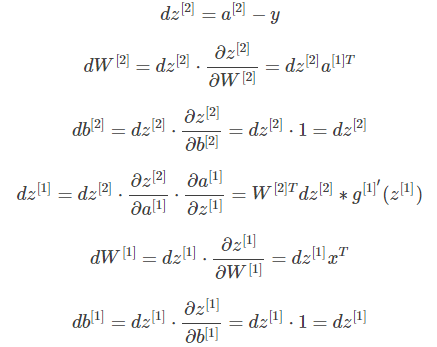
Ag课程的总结（深层神经网络）

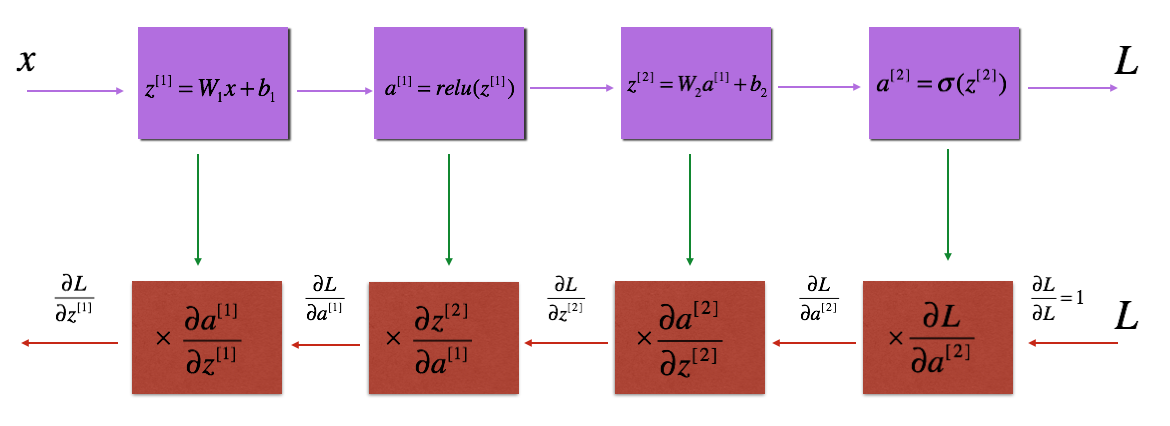
已知 \(AL\) 和 \(J\)，先求出 \(dAL\)：

\(dAL = -(np.divide(Y, AL) - np.divide(1-Y, 1-AL)) ​\)

---> \(dZL = dAL * sigmod'(Z^{[L]}) = dAL*s*(1-s) ​\)

---> \(dWL=\frac{1}{m}dZL·A^{[L-1]T}​\)

---> \(dbL=\frac{1}{m}np.sum(dZL, axis=1, keepdims=True) ​\)

---> \(dA^{[L-1]} = W^{[L]T}·dZ^{[L]}​\)

===>

\(dZ^{[l]} = dA^{[l]} * g'(Z^{[l]})\) （\(l \in [L-1 , 1]\) ，\(relu'(Z^{[l]}) = np.int64(A^{[l]} > 0)\) ）

---> \(dW^{[l]} = \frac{1}{m}dZ^{[l]}·A^{[l-1]T}\)

---> \(db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]}, axis=1, keepdims=True) ​\)

---> \(dA^{[l-1]} = dZ^{[l]}·W^{[l]} = W^{[l]T}·dZ^{[l]}\)

……

……