深度学习基础知识

第一讲 深度学习概述

1.1 深度学习的引出

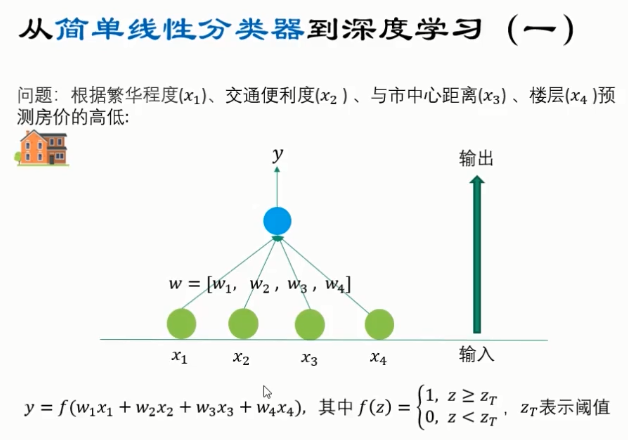
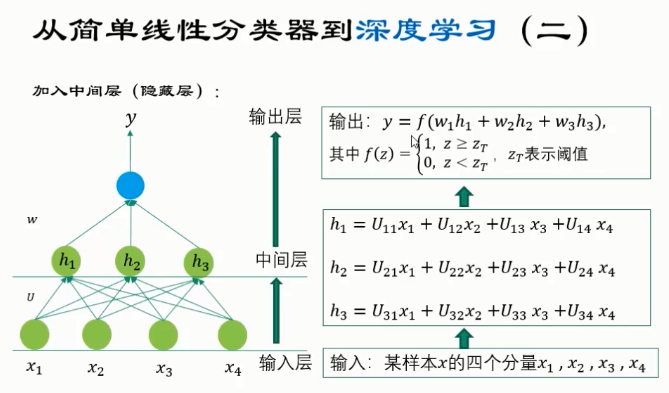
特点：

  • 通过 组合低层特征，形成了更加抽象的 高层特征。

  • 表达式中的 u，w参数需要在训练中通过 反向传播多次迭代调整，使得整体的 分类误差最小。

  • 深度学习网络往往 包含多个中间层（隐藏层），且网络结构要更复杂一些。

 

1.2 数据集及其拆分

  • Iris（鸢尾花）数据集

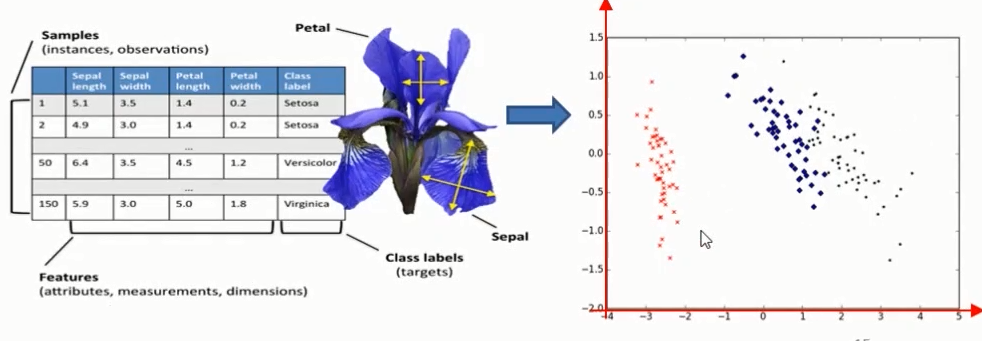
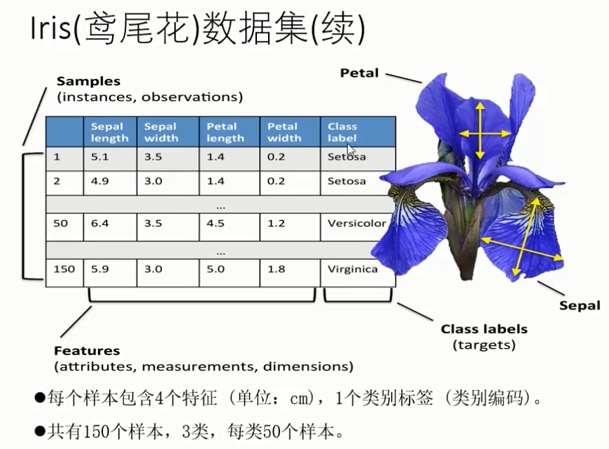
  • 分类特征：花萼和花瓣的宽度和长度

数据集在数学上通常表示为 $\{(x_1,y_1),(x_2,y_2),...,(x_i,y_i),...,(x_m,y_m)\}​$

  • 其中  $x_i$  为样本特征。由于样本（即一行）一般有多个特征，因而 $x_i = \{x_i^1, x_i^2,..., x_i^n\} ​$

  • 而 $y_i$  表示 样本i 的 类别标签。

类别标签的ground truth 与 gold standard

  • ground truth：翻译为地面实况。机器学习领域一般用于表示 真实值、标准答案 等，表示 通过 直接观察收集到 的真实结果。

  • gold standard：金标准，医学上一般指诊断疾病 公认的最可靠的方法。

  • 机器学习领域更倾向于使用ground truth，如果用gold standard则表示可以很好地代表ground truth。

 

1.21 数据集与有监督学习

有监督学习中数据通常分成 训练集、测试集 两部分。

  • 训练集( training set)：用来训练模型，即被用来 学习 得到系统的 参数取值。

  • 测试集( testing set)：用于最终报告模型的评价结果，因此在训练阶段测试集中的样本应该是不可见的。

  • 对训练集做进一步划分为 训练集、验证集 validation set。

    • 验证集：与测试集类似，也是用于评估模型的性能。

    • 区别：是 验证集 主要 用于 模型选择 和 调整超参数，因而一般不用于报告最终结果。

 

1.22 训练集测试集拆分

  • 留出法( Hold-out Method)数据拆分步骤

            1.将数据随机分为两组，一组做为训练集，一组做为测试集

            2.利用训练集训练分类器,然后利用测试集评估模型，记录最后的分类准确率为此分类器的性能指标

  • K折交叉验证

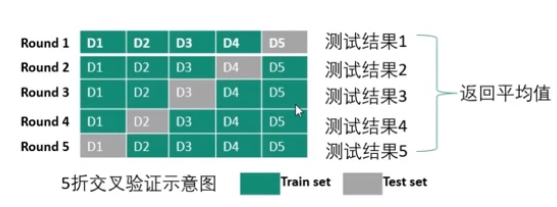
  •  过程

    1. 数据集被分成K份 (K通常取5或者10)

    2. 不重复地每次取其中 一份 做测试集，用其他 K-1 份做训练集训练，这样会得到K个评价模型

    3. 将上述步骤2中的 K次评价 的性能 均值 作为最后评价结果

  • 优点：
    • K折交叉验证的上述做法，有助于提高评估结果的稳定性
  •  分层抽样策略（Stratified k-fold）

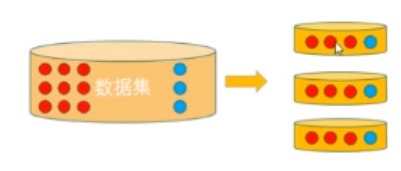
  • 过程：

    • 将数据集划分成k份，特点在于，划分的k份中 ——

    • 每一份内各个类别数据的比例 和 原始数据集中各个类别的比例 相同。

 

1.23 K折交叉验证的应用—用网格搜索来调超参数

  • 什么是超参数？

    • 指在学习过程之前 需要设置其值的一些变量

    • 而不是通过训练得到的参数数据。如深度学习中的学习速率（learning rate）等就是超参数。

  • 什么是网格搜索?

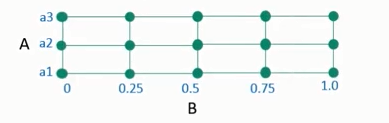
    • 假设模型中有2个超参数：A和B。

    • A的可能取值为 ${a1,a2,a3}$；

    • B的可能取值为连续的，如在区间[0-1]。由于B值为连续，通常进行离散化，如变为 {0, 0.25, 0.5, 0.75, 1.0}

    • 如果使用网格搜索，就是尝试各种可能的 (A,B)对值，找到 能使的模型取得最高性能的 (A,B)值对。

网格搜索与K折交叉验证结合调整 超参数 的具体步骤：

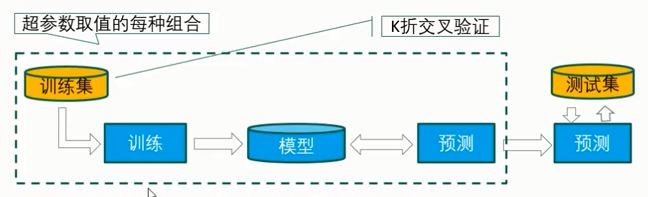
  1. 确定评价指标（准确率等）

  2. 对于超参数取值的每种组合，在 训练集 上使用 交叉验证的方法 求得 其K次评价的性能均值

  3. 最后，比较哪种超参数取值组合的性能最好，从而得到最优超参数的取值组合。

 

1.3 分类及其性能度量

1.31 分类

  • 分类问题是有监督学习的一个核心问题。分类解决的是要预测样本属于哪个或者哪些预定义的类别。此时输出变量通常取有限个离散值。

  • 分类的机器学习的两大阶段

    1. 从训练数据中学习得到一个 分类决策函数 或 分类模型，称为 分类器( classifier)；

    2. 利用学习得到的分类器对新的输入样本进行类别预测。

  • 两类分类问题 与 多类分类问题：

    • 多类分类问题也可以转化为两类分类问题解决，如采用 一对其余（One-Vs-Rest） 的方法：

    • 将其中一个类标记为正类，然后将剩余的其它类都标记成负类。

1.32 分类性能度量 ☆☆☆

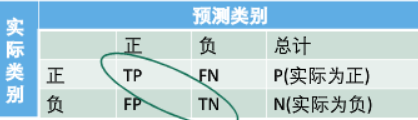
  • 假设只有两类样本，即正例(positive) 和 负例 (negative)。
  • 通常以关注的类为正类，其他类为负类。

 

  • 表中AB模式：

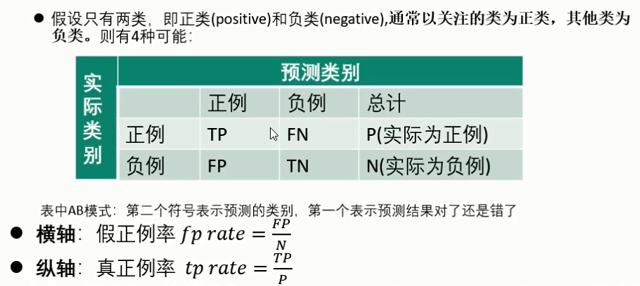
    • 第二个符号表示：预测的类别 ( Positive or Negative )

    • 第一个表示：预测结果 ( True or False)

  • 分类准确率( accuracy)：分类器正确分类的样本数与总样本数之比：

    • $accuracy = \frac{TP+TN}{P+N}$

  • 精确率( precision)：反映了模型 判定的正例 中 真正正例 的比重。

    • 在垃圾短信分类器中，是指 预测出 的垃圾短信中真正垃圾短信的比例。

    • $precison = \frac{TP}{TP+FP}$

  • 召回率{ recall)：反映了 总正例 中被模型 正确判定正例 的比重。

    • 医学领域也叫做灵敏度( sensitivity)。在垃圾短信分类器中,指所有真的垃圾短信被分类器正确找出来的比例。

    • $recall = \frac{TP}{P}$

  • P-R 曲线 

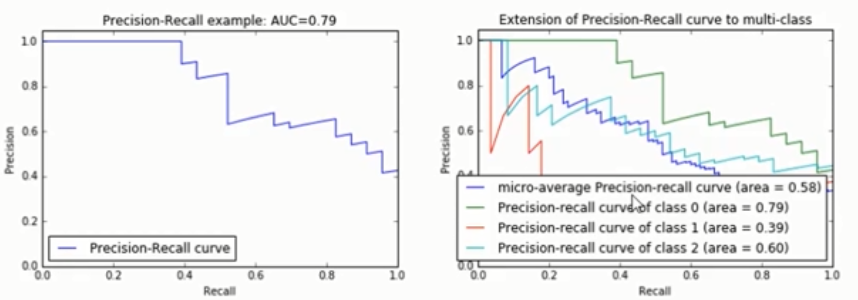
  • Area( Area Under Curve，或者简称AUC)：

    • Area的定义（p-r曲线下的面积）：

      • $Area = \int_0^1p(r)dr$

    • 有助于弥补P、R的单点值局限性，可以反映全局性能。

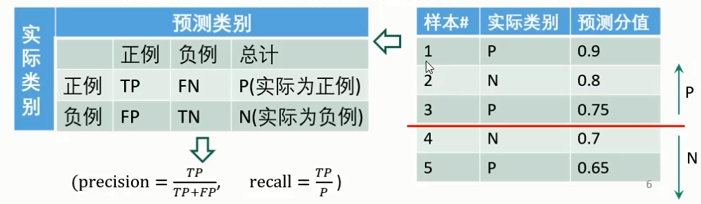
  • 如何绘制 P-R曲线

    • 要得到PR曲线，需要一系列 Precision和Recall的值。这些系列值是通过 阈值 来形成的。对于每个测试样本，分类器一般都会给了“Score”值，表示该样本多大概率上属于正例。

  • 步骤：

    1. 从高到低将“ Score"值排序，并依此作为阈值 threshold；

    2. 对于每个阈值，“ Score"值大于或等于这个 threshold的测试样本被认为正例，其它为负例。从而形成一组预测数据。（每个样本设置不同阈值，算出precison和recall，从而形成一组数据）

  • F值 ☆☆☆

    • F 值 ($F_\beta-score$) 是 精确率 和 召回率 的 调和平均：

      • $F_\beta-score=\frac{(1+\beta^2)*precison*recall}{(\beta^2*precision+recall)}$

      • $\beta一般大于0。当\beta=1时，退化为 F1$ 

      • $F_1$ 是最常用的 评价指标，即 表示二者同等重要

  • ROC（受试者工作特征曲线，receiver operating characteristic curve）

    • 描绘了分类器在 $tp rate$ （真正正例占总正例的比率，反映命中概率，纵轴)  和

    • $fp rate$（错误的正例占反例的比率，反映误诊率、假阳性率、虚惊概率，橫轴)间的trade-off。

    • ROC曲线绘制 和 P-R曲线类似。

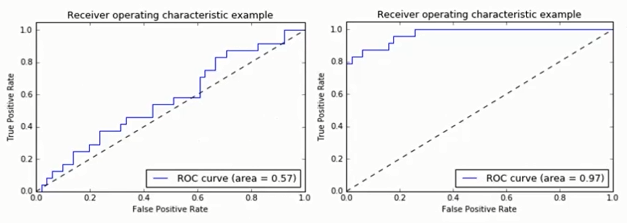
  • ROC- AUC( Area Under Curve)定义为ROC曲线下的面积

    • AUC值提供了分类器的一个整体数值。通常AUC越大,分类器更好。

    • 取值范围为[0,1]

  • 分类性能可视化

    • 混淆矩阵的可视化：可用热图（heatmap）直观展现类别的混淆情况

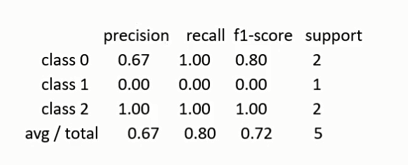
    • 分类报告：显示每个类的分类性能，包括每个类标签的精确率、召回率、F1值等。

1.4 回归问题及其性能度量

1.41 回归分析( regression analysis)

回归分析( regression analysis)：

  • 是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法

  • 和分类问题不同：

    • 回归 通常输出为 一个实数数值。

    • 分类 通常输出为 若干指定的类别标签。

1.42 常用的回归性能度量方法

  • 平均绝对误差 MAE (mean_absolute_error)

    • MAE ( Mean absolute error) 是 绝对误差损失( absolute error loss)的期望值。　　

    • 如果 $\hat{y_i}$ 是 第 $i$ 个样本的 预测值，$y_i$是相应的真实值，那么在 $n_samples$个测试样本上的 平均绝对误差 (MAE) 的定义如下：

      • $MAE(y, \hat{y}) = \frac{1}{n_{sample}}\sum_{i=0}^{n_{samplee}-1}|y_i - \hat{y_i}|$

  • 均方误差 MSE (mean_squared_error) 及 均方根差 RMSE

    • MSE( Mean squared error)，该指标对应于 平方误差损失( squared errorloss)的期望值。

    • 如果 $\hat{y_i}$ 是 第 $i$ 个样本的 预测值，$y_i$是相应的真实值，那么在 $n_samples$个测试样本上的 均方差 的定义如下：

      • $MSE(y, \hat{y}) = \frac{1}{n_{sample}}\sum_{i=0}^{n_{samplee}-1}|y_i - \hat{y_i}|^2$

    • 均方根差RMSE：是MSE的平方根

  • logistic回归损失（二类）

    • 简称 Log loss，或交叉熵损失( cross-entropy loss)

      • 常用于评价 逻辑回归LR 和 神经网络

    • 对于二类分类问题：
    1. 假设某样本的真实标签为 y (取值为0或1)，概率估计为 $p = pr(y = 1)$

    2. 每个样本的 log loss 是对 分类器 给定 真实标签 的 负log似然估计(negative log-likelihood)

      • $L_{log}(y, p) = -log(pr(y|p)) = -(ylog(p) + (1- y)log(1-p))​$

    3. 实例：

  • logistic回归损失（多类）

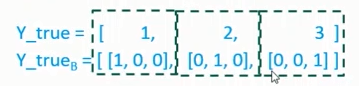
    • 对于多类问题( multiclass problem)，可将样本的真实标签( true label) 编码成 1-of-K( K为类别总数)的 二元指示矩阵Y： 

    • 转换举例：假设 K = 3，即三个类

    • 假设模型对测试样本的概率估计结果为P，则在测试集（假设测试样本总数为N）上的交叉熵损失表示如下：

      • $L_{log}(Y, P) = -\frac{1}{N}\sum_{k=0}^{k-1}y_{i, k}logp_{i, k}$

      •  $y_{i,k}$ ：表示第 $i$ 个样本的第 $k$ 个标签的 真实值 

        • 即ground truth，具体含义为第 $i$ 个样本，是否属于第 $k$ 个标签，注意由于表示为 “1-of-K" 模式，因此每个样本只有其中一个标签值为1，其余均为0。

      • $p_{i,k}$ ：表示模型对第 $i$ 个样本的 第 $k$ 个标签的 预测值。

    • 举例：6个样本，三个类

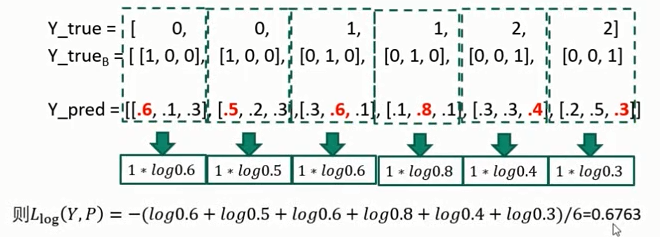
  • 回归评价的真实标签（即ground truth）如何获得？

    • MAE，RMSE(MSE) 常用于评分预测评价，eg 很多提供推荐服务的网站都有一个让用户给物品打分的功能预测用广对物品评分的行为称为 评分预测。

1.5 一致性的评价方法(nlp用不到)

  • 一致性评价：是指对两个或多个相关的变量进行分析，从而衡量其相关性的密切程度。

  • 问题举例：

  • 假设两评委( rater)对5部电影的评分如下，则二者的一致如何?

  • rater1=[0.5,1.6,25,25,24]

  • rater2=[1.5,26,35,3.5,34]

  • 皮尔森相关系数法

应用背景：

  • 用来衡量两个用户之间兴趣的 一致性

  • 用来衡量 预测值与真实值 之间的 相关性

  • 既适用于离散的、也适用于连续变量的 相关分析

X 和 Y 之间的皮尔森相关系数计算公式：

  • $\rho_{X,Y} = \frac{cov(X,Y)}{\sigma_X\sigma_Y} = \frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y}$

  • 其中，$cov(X,Y)$ 表示X和Y之间的 协方差( Covariance)

  • $\sigma_X$ 是X的均方差，$\mu_X$ 是 X 的均值，E表示数学期望

  • 取值区间为[-1,1]。-1：完全的负相关,+1：表示完全的正相关,0：没有线性相关。

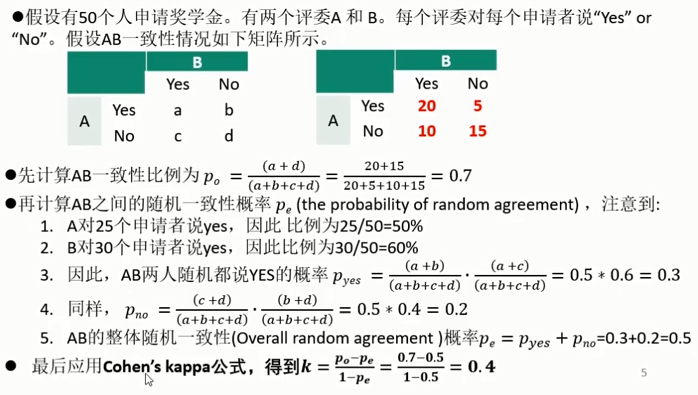
  • Cohen's kappa相关系数

  • 与 皮尔森相关系数的区别：Cohens kappa相关系数，通常用于离散的分类的一致性评价。

  • 其通常被认为比两人之间的简单一致百分比更强壮，因为 Cohen's kappa考虑到了:二人之间的随机一致的可能性

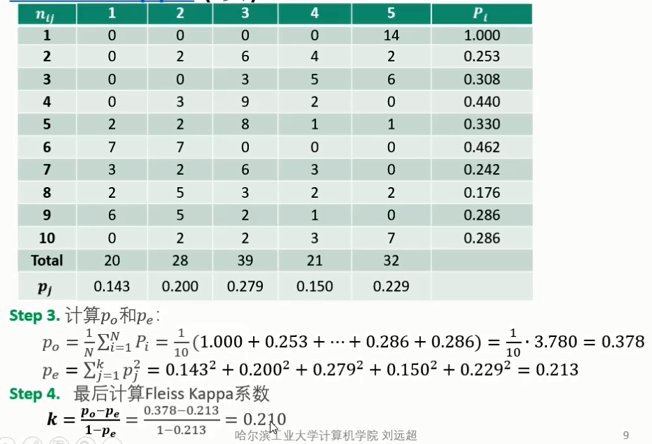
  • 如果评价者多于2人时，可以考虑使用 Fleiss' kappa

  • Cohen's kappa的计算方法： 

 

  • kappa score是一个介于-1到+1之间的数。

  •  Fleiss' Kappa

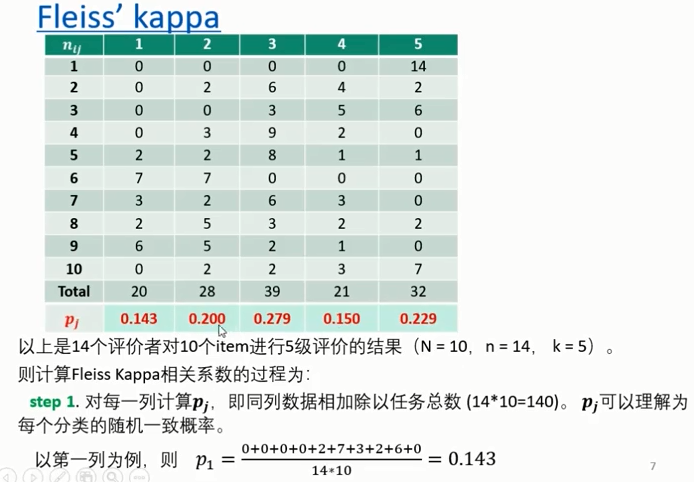
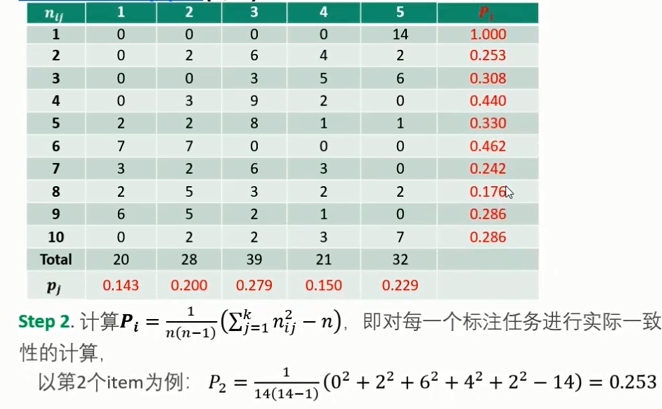
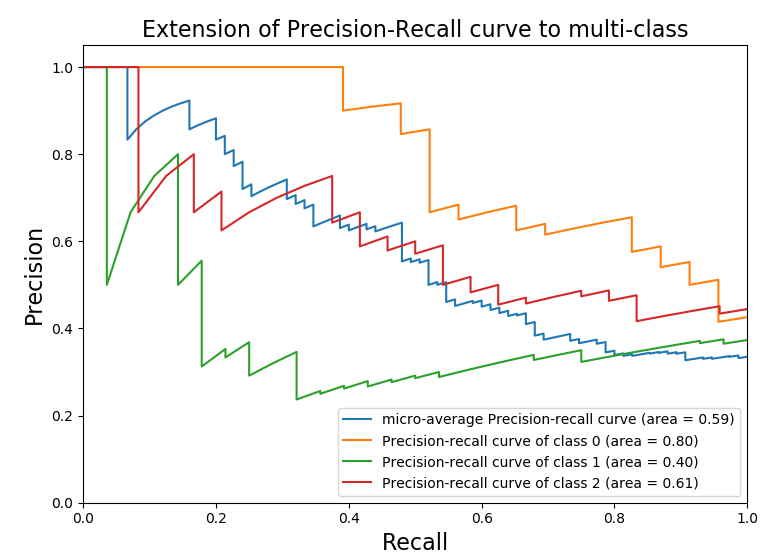
1.6 实例：绘制PR曲线

#利用鸢尾花数据集绘制P-R曲线
print(__doc__)      #打印注释

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm, datasets
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import average_precision_score
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier  #一对其余（每次将一个类作为正类，剩下的类作为负类）

# from sklearn.cross_validation import train_test_split  #适用于anaconda 3.6及以前版本
from sklearn.model_selection import train_test_split     #适用于anaconda 3.7

#以iris数据为例，画出P-R曲线
iris = datasets.load_iris()
X = iris.data    #150*4
y = iris.target  #150*1

# 标签二值化,将三个类转为001, 010, 100的格式.因为这是个多类分类问题，后面将要采用
#OneVsRestClassifier策略转为二类分类问题
y = label_binarize(y, classes=[0, 1, 2])    #将150*1转化成150*3
n_classes = y.shape[1]                      #列的个数，等于3
print (y)

# 增加了800维的噪声特征
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape

X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]   #行不变，只增加了列，150*804

# 训练集和测试集拆分，比例为0.5
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5, random_state=random_state) #随机数，填0或不填，每次都会不一样

# 一对其余，转换成两类，构建新的分类器
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True, random_state=random_state))
#训练集送给fit函数进行拟合训练，训练完后将测试集的样本特征注入，得到测试集中每个样本预测的分数
y_score = classifier.fit(X_train, y_train).decision_function(X_test)

# Compute Precision-Recall and plot curve
#下面的下划线是返回的阈值。作为一个名称：此时“_”作为临时性的名称使用。
#表示分配了一个特定的名称，但是并不会在后面再次用到该名称。
precision = dict()
recall = dict()
average_precision = dict()
for i in range(n_classes):
    #对于每一类，计算精确率和召回率的序列（:表示所有行，i表示第i列）
    precision[i], recall[i], _ = precision_recall_curve(y_test[:, i],  y_score[:, i])
    average_precision[i] = average_precision_score(y_test[:, i], y_score[:, i])#切片，第i个类的分类结果性能

# Compute micro-average curve and area. ravel()将多维数组降为一维
precision["micro"], recall["micro"], _ = precision_recall_curve(y_test.ravel(),  y_score.ravel())
average_precision["micro"] = average_precision_score(y_test, y_score, average="micro") #This score corresponds to the area under the precision-recall curve.

# Plot Precision-Recall curve for each class
plt.clf()#clf 函数用于清除当前图像窗口
plt.plot(recall["micro"], precision["micro"],
         label='micro-average Precision-recall curve (area = {0:0.2f})'.format(average_precision["micro"]))
for i in range(n_classes):
    plt.plot(recall[i], precision[i],
             label='Precision-recall curve of class {0} (area = {1:0.2f})'.format(i, average_precision[i]))

plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05]) #xlim、ylim：分别设置X、Y轴的显示范围。
plt.xlabel('Recall', fontsize=16)
plt.ylabel('Precision',fontsize=16)
plt.title('Extension of Precision-Recall curve to multi-class',fontsize=16)
plt.legend(loc="lower right")#legend 是用于设置图例的函数
plt.show()

第二讲 特征工程

2.1 特征工程

什么是特征工程？

引自知乎: “数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。

深度学习也要用到 特征，需要对 输入的特征 进行 组合变换等处理。

2.11 自动分词

  • 自动分词：就是将用自然语言书写的文章、句段经计算处理后，以词为单位 给以输出，为后续加工处理提供先决条件。

  • 词形规范化 的两种形式：词根提取与词形还原
    • 词根提取( stemming)：是抽取词的词干或词根形式（不一定能够表达完整语义）。

    • 词形还原( lemmatization)：是把词汇还原为一般形式（能表达完整语义）。如将“ drove"处理为"drive"。

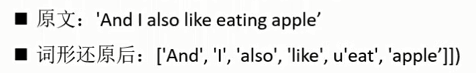
2.12 词性标注

  • 词性标注 (part-of- speech tagging)：

    • 是指为分词结果中的 每个单词 标注一个正确的词性的程序

    • 也即确定每个词是 名词、动词、形容词 或者 其他词性的过程。

 

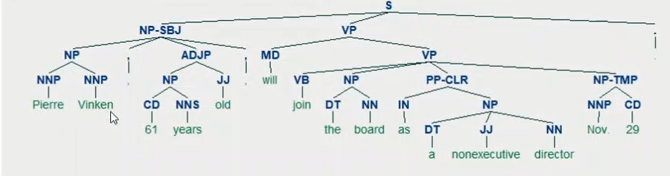
2.13 句法分析

  • 句法分析( Syntactic analysis)：

  • 其基本任务是确定句子的 句法结构 或者 句子中词汇之间的 依存关系。

 

2.14 自然语言处理工具

  • NLTK

Natural Language Toolkit（自然语言处理工具包）是在NLP领域中最常用的一个 Python库。

提供了很多文本处理的功能: 

  1. Tokenization（词语切分，单词化处理）

  2. Stemming（词干提取）

  3. Tagging（标记，如词性标注）

  4. Parsing（句法分析）

此外，还提供了50多种语料和词汇资源的接口，如 Word Net等。

  • Text Processing API

 支持如下功能：

  1. 词根提取与词形还原( Stemming& Lemmatization)

  2. 情感分析( Sentiment Analysis)

  3. 词性标注和语块抽取( Tagging and chunk Extraction)

  4. 短语抽取和命名实体识别( Phrase Extraction& Named Entity Recognition)

与NLTK不同，Text Processing API的使用无需安装程序，只需将输入的文本信息通过http post方式联网传递给该网络接口即可。

  • TextBlob工具

  • 中文处理工具 jieba

 功能：

  • 分词（包括并行分词、支持自定义词典）

  • 词性标注

  • 关键词提取

2.2 向量空间模型及文本相似度计算

2.21 文档的向量化表示：BOW假设和VSM模型

为了便于计算文档之间的相似度，需把 文档转成统一空间的向量

  • BOW(bag- of-words model)：为了计算文档之间的相似度，假设可以忽略文档内的单词顺序和语法、句法等要素，将其仅仅看作是若干个词汇的集合。

  • VSM( Vector space model)：即向量空间模型。其是指在BOW词袋模型假设下，将每个文档表示成同一向量空间的向量。

 

  • 举例：

2.22 停用词

英文名称： Stop words

  • 停用词通常是非常常见且实际意义有限的词, 如英文中“the",“a", "of",“an”等;中文中“的”、“是”、“而且”等。几乎可能出现在所有场合，因而对某些应用如信息检索、文本分类等区分度不大。

  • 在信息检索等应用中，这些词在构建向量空间时通常会被过滤掉。因此这些词也被称为停用词。

  • Tip：但在某些应用如短语搜索 phrase search中，停用词可能是重要的构成部分，因此要避免进行停用词过滤。

2.23 N-gram模型

  • N-gram：
    • N-gram 是一个基于概率的判别模型，它的输入是一句话（单词的顺序序列），输出是这句话的概率，即这些单词的联合概率（joint probability）。
    • N-gram本身也指一个由 N 个单词组成的集合，各单词具有先后顺序，且不要求单词之间互不相同。
    • 通常是指 一段文本或语音中连续N个项目(item)的序列。项目(item)可以是单词、字母、碱基对等。

  • N=1 称为 uni-gram，N=2 称为 bi-gram，N=3 称为 tri-gram，以此类推。

  • 举例：对于文本 'And I also like to eat apple'
    • Uni-gram： And, I, also, like, to, eat, apple
    • Bi-gram：And l, I also, also like, like to, to eat, eat apple
    • Tri-gram：And I also, I also like, also like to, like to eat, to eat apple

  • 20世纪80年代，N-gram被广泛地应用在 拼写检查、输入法 等应用中，90年代以后，N-gram得到新的应用，如自动分类信息检索等。即将 连续的若干词作为VSM中的维度，用于表示文档。

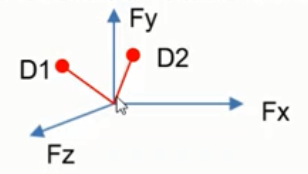
2.24 文档之间的欧式距离

  • 欧氏距离( euclidean metric) 是一个通常采用的距离定义，指在n维空间中两个点之间的真实距离。

  • 公式：$d_{12} = \sqrt{\sum_{k=1}^n (x_{1k} - x_{2k})^2}$

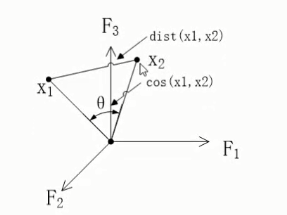
2.25 文档之间的余弦相似度

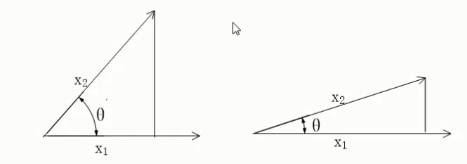
  • 通过计算 两个向量的夹角余弦值 来评估他们的相似度。余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似。

  • $cos(\theta) = \frac{\sum_{k=1}^n(x_{1k} \times x_{2k} )}{\sqrt{{\sum_{k=1}^n}(x_{1k})^2}\times \sqrt{{\sum_{k=1}^n}(x_{2k})^2}} = \frac{x_1 \cdot x_2}{||x_1||\times||x_2||}​$

2.26 Ti-idf词条权重计算

  • 背景：特征向量 里某些高频词在文集内其他文档里面也经常出现。它往往太普遍，对区分文档起的作用不大。

  • 例如：

    • D1:' Jobs was the chairman of Apple Inc.',

    • D2: 'I like to use apple computer',

  • 这两个文档都是关于苹果电脑的，则词条 apple对分类意义不大。因此 有必要抑制 那些 在很多文档中都出现了的词条的权重。

  • 在 $tf-idf$ 模式下，词条t 在文档d中的权重计算为 $w(t)=tf(t, d) * idf(t)$。

    • $tf(t,d)$：表示为 词条t 在 文档d 中的出现频率

      • 通过统计得到

    • $idf(t)$ ：表示与包含词条t 的文档数目成反比 (inverse document frequency)

      • $idf(t) = (log\frac{n_d}{1+df(t)} + 1)$

      • $n_d$：表示文档总数，$df(t)$：表示 包含该词条t  的文档数

      • (optional) 数据平滑问题：为了防止分母 $df(t)$ 为零

      • $idf(t) = (log\frac{1+n_d}{1+df(t)} + 1)$

  • $tf-idf$词条权重计算 举例：

2.3 特征处理(特征缩放、选择及降维)

2.31 特征值的缩放

特征值缩放( Feature scaler)也可以称为 无量纲处理。主要是对每个列，即同一特征维度的数值进行规范化处理。

应用背景：

  • 不同特征(列)可能不属于同一量纲，即特征的规格不一样。例如，假设特征向量由两个解释变量构成，第一个变量值范围[0,1],第二个变量值范围[0,100]。

  • 如果某一特征的方差数量级较大，可能会主导目标函数，导致其他特征的影响被忽略。

常用方法：

  • 标准化法

    • 前提：特征值服从正态分布

    • 需要计算特征的 均值X.mean 和 标准差X.std：

    • $X_{scale} = \frac{(X(axis=0) - X.mean(axis=0))}{X.std(axis=0)}​$

    • 标准差(Standard Deviation)，又称均方差

      • 用 $\sigma$ 表示，是方差的算术平方根。$\sigma = \sqrt{{\frac{1}{N}\sum_{i=0}^{N-1}(x_i - \mu)}^2 }$

      • 标准差：反应一个数据集的离散程度。

      • 例如两组数的集合{0,5,9,1,4}和{5,6,8,9}其平均值都是7，但第二个集合具有较小的标准差。

  • 区间缩放法

    • 区间缩放法利用了 边界值信息，将 特征的取值区间 缩放到某个特定范围。假设max和min为希望的调整后范围，则

      • $X_{scaled} = \frac{(X(axis=0) - X.min(axis=0))}{(X.max(axis=0) - X.min(axis=0))} *(max - min)+min $ 

    • 由于希望的调整后范围一般为[0, 1]。此时，公式变为：

      • $X_{scaled} = \frac{(X(axis=0) - X.min(axis=0)) }{(X.max(axis=0) - X.min(axis=0))}​$ 

 

2.32 特征值的归一化

  • 或称规范化（Normalizer）

  • 归一化是依照 特征矩阵的 行（即样本）处理数据

    • 其目的在于 样本向量 在 点乘运算 或 计算相似性时，拥有统一的标准

    • 也就是说 都转化为“单位向量”。即使每个样本的范式(norm)等于1。

  • 规则为L1 norm 的 归一化 公式如下：

    • $x^{'} = \frac{x}{\sum_{j=0}^{n-1}|x_j|}​$ 

  • 规则为 L2 norm 的 归一化 公式如下：

    • $x^{'} = \frac{x}{\sum_{j=0}^{n-1}x_j^2}​$ 　　

 

2.33 定量特征的二值化

应用背景：

  • 对于某些定量特征，需要 将 定量信息 转为 区间划分。如将考试成绩转为“及格”或“不及格”

方法：

  • 设定一个阈值，大于或者等于阈值的赋值为1，小于阈值的赋值为0，公式表达：

$$
x^{'} =
\begin{cases}
1, x>=threshold \\
0, x < threshold
\end{cases}
$$

 

2.34 缺失特征值的弥补计算

背景：

  • 数据获取时，由于某些原因缺少某些数值，需要进行弥补。

常见的弥补策略：

  • 利用 同一特征 的 均值 进行弥补。

举例：counts=[[1,0,1],

                         [2,0,0],

                         [3,0,0],

                         [NaN,0,0]]

则，NaN可以弥补为同列上其他数据的均值，即(1+2+3)/3=2

 

2.35 创建多项式特征

 

2.36 特征选择

  • 什么是特征选择？选择对于学习任务（如分类问题）有帮助的若干特征。

  • 为什么要进行特征选择？

    1. 降维以提升模型的效率

    2. 降低学习任务难度　　

    3. 增加模型的可解释性。

  • 特征选择的角度：

    1. 特征是否发散：对于不发散的特征，样本在其维度上差异性较小

    2. 特征与目标的相关性：应当优先选择与目标 相关性高的特征

  •  几种常见的特征选择方法：
  • 方差选择法

    • 原理：方差非常小的特征维度，对于样本的区分作用很小，可以剔除。

    • 例如，假设数据集为布尔特征，想去掉那些，超过80%情况下为1或者为0的特征。由于布尔特征是 Bernoulli(伯努利)随机变量，其方差可以计算为Var[x]=p*(1-p)，因此阈值为0.8*(1-0.8)=0.16

  • 皮尔森相关系数法

    • 皮尔森相关系数( Pearson correlation coefficient)：显示两个随机变量之间线性关系的强度和方向。

    • 计算完毕后，可以将与目标值相关性较小的特征过滤掉。

    • Tip: Pearson相关系数，对线性关系比较敏感。如果关系是非线性的，即便两个变量具有一一对应的关系，Pearso相关性也可能会接近0。

  • 基于森林的特征选择法

    • 其原理是某些分类器，自身提供了特征的重要性分值。因此可以直接调用这些分类器，得到特征重要性分值，并排序。

  • 递归特征消除法

    1. 首先在初始特征或者权重特征集合上训练。通过学习器返回的coef_属性或者 feature_ importances_属性来获得每个特征的重要程度

    2. 然后最小权重的特征被移除。

    3. 这个过程递归进行，直到希望的特征数目满足为止。

 

2.37 特征降维

降维本质上是从一个维度空间映射到另一个维度空间。

常见特征降维方法：

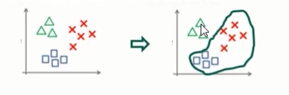
  • 线性判别分析( (Linear Discriminant analysis，简称LDA)是一种 监督学习 的降维技术，即数据集的每个样本有类别输出。

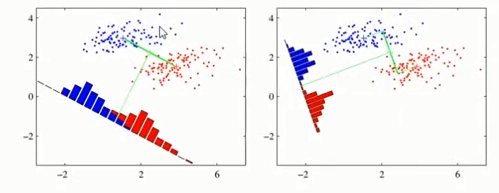
    • LDA的基本思想: “投影后类内方差最小，类间方差最大”。

    • 即将数据在 低维度 上进行投影，

      • 投影后希望 同类数据的投影点尽可能接近，

      • 而 不同类数据 的 类别中心 之间的 距离尽可能的大。(右图好)

  • 主成分分析( principal component analysis)是一种 无监督的降维方法。

  • 采用数学变换，把给定的一组相关特征维度，

  • 通过 线性换转 成另一组不相关的维度(即 principal components)，

  • 这些新的维度照 方差 依次递减的顺序排列：形成第一主成分、第二主成分等。

  • 应用：高维数据在二维平面上进行展示。

 

2.4 实例：使用sklearn对文档进行向量化

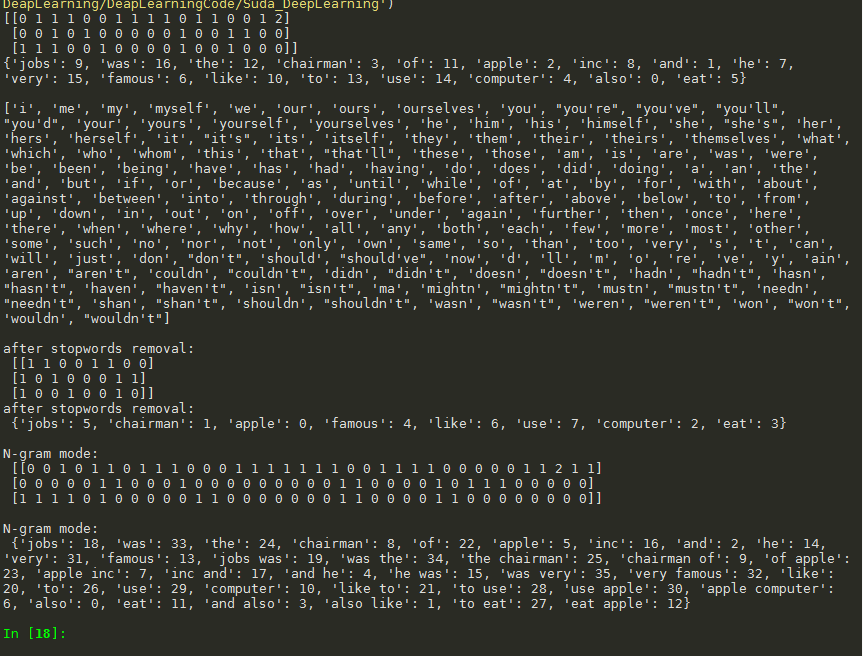
# -*- coding: utf-8 -*-
"""
Created on Tue Jun  2 15:45:18 2020

@author: douzi
"""

"""
演示内容：文档的向量化
"""
from sklearn.feature_extraction.text import CountVectorizer
corpus = [
'Jobs was the chairman of Apple Inc., and he was very famous',
'I like to use apple computer',
'And I also like to eat apple'
]

#未经停用词过滤的文档向量化
vectorizer =CountVectorizer()
print(vectorizer.fit_transform(corpus).todense())  #转化为完整特征矩阵
print(vectorizer.vocabulary_)
print(" ")


#经过停用词过滤后的文档向量化
import nltk
nltk.download('stopwords')       # 没有这个文件，就需要下载 
stopwords = nltk.corpus.stopwords.words('english')
print (stopwords)

print(" ")
vectorizer =CountVectorizer(stop_words='english')
print("after stopwords removal:\n", vectorizer.fit_transform(corpus).todense())
print("after stopwords removal:\n", vectorizer.vocabulary_)

print(" ")
#采用ngram模式进行文档向量化
vectorizer =CountVectorizer(ngram_range=(1,2))    #表示从1-2，既包括unigram，也包括bigram
print("N-gram mode:\n",vectorizer.fit_transform(corpus).todense())  #转化为完整特征矩阵
print(" ")
print("N-gram mode:\n",vectorizer.vocabulary_)

2.5 实例：使用sklearn进行量纲缩放（标准化和区间缩放法）

# -*- coding: utf-8 -*-

"""
演示内容：量纲的特征缩放
（两种方法：标准化缩放法和区间缩放法。每种方法举了两个例子：简单二维矩阵和iris数据集）
"""
#方法1：标准化缩放法 例1：对简单示例二维矩阵的列数据进行
from sklearn import preprocessing   
import numpy as np  
#采用numpy的array表示，因为要用到其mean等函数，而list没有这些函数
X = np.array([[0, 0], 
              [0, 0], 
              [100, 1], 
              [1, 1]])  
# calculate mean  
X_mean = X.mean(axis=0)    # 计算每一列的平均值
# calculate variance   
X_std = X.std(axis=0)      # 计算每一列的标准差
#print (X_std)
# standardize X  
X1 = (X-X_mean)/X_std
print (X1)
print ("")
 
# we can also use function preprocessing.scale to standardize X  
X_scale = preprocessing.scale(X)  
print (X_scale)
 
 
#方法1： 标准化缩放法 例2：对iris数据二维矩阵的列数据进行。这次采用一个集成的方法StandardScaler
from sklearn import datasets
iris = datasets.load_iris()
X_scale = preprocessing.scale(iris.data)  
print (X_scale)
 
#方法2： 区间缩放法 例3：对简单示例二维矩阵的列数据进行
from sklearn.preprocessing import MinMaxScaler
 
data = [[0, 0], 
        [0, 0], 
        [100, 1], 
        [1, 1]]
 
scaler = MinMaxScaler()
print(scaler.fit(data))
print(scaler.transform(data))
 
#方法2： 区间缩放法 例4：对iris数据二维矩阵的列数据进行
from sklearn.preprocessing import MinMaxScaler
 
data = iris.data
 
scaler = MinMaxScaler()
print(scaler.fit(data))
print(scaler.transform(data))

 

posted @ 2020-05-31 20:21  douzujun  阅读(2018)  评论(0)  编辑  收藏  举报