Neural Networks and Deep Learning (week3)浅层神经网络(Shallow neural networks)
3.1 神经网络概述(Neural Network Overview )
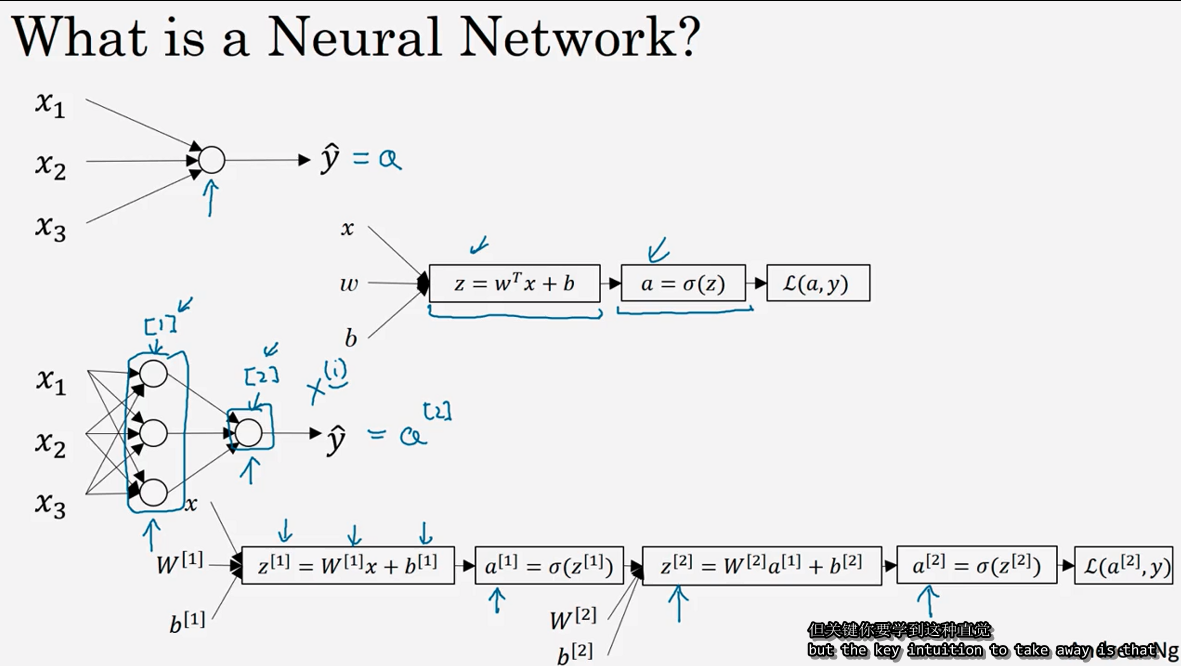
(神经网络中,我们要反复计算a和z,最终得到最后的loss function)

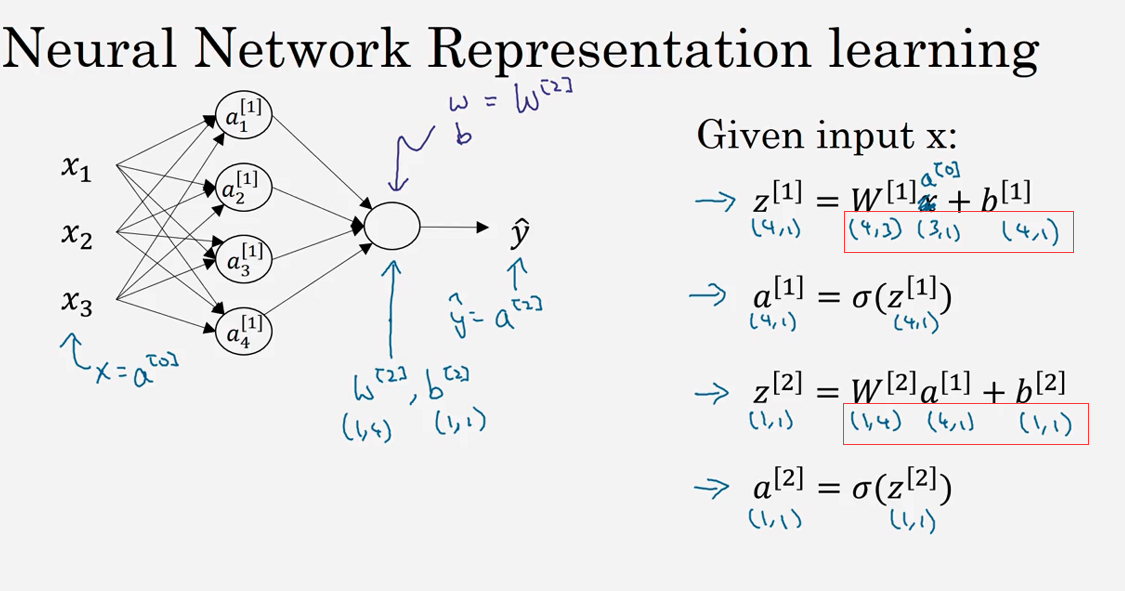
3.2 神经网络的表示(Neural Network Representation)
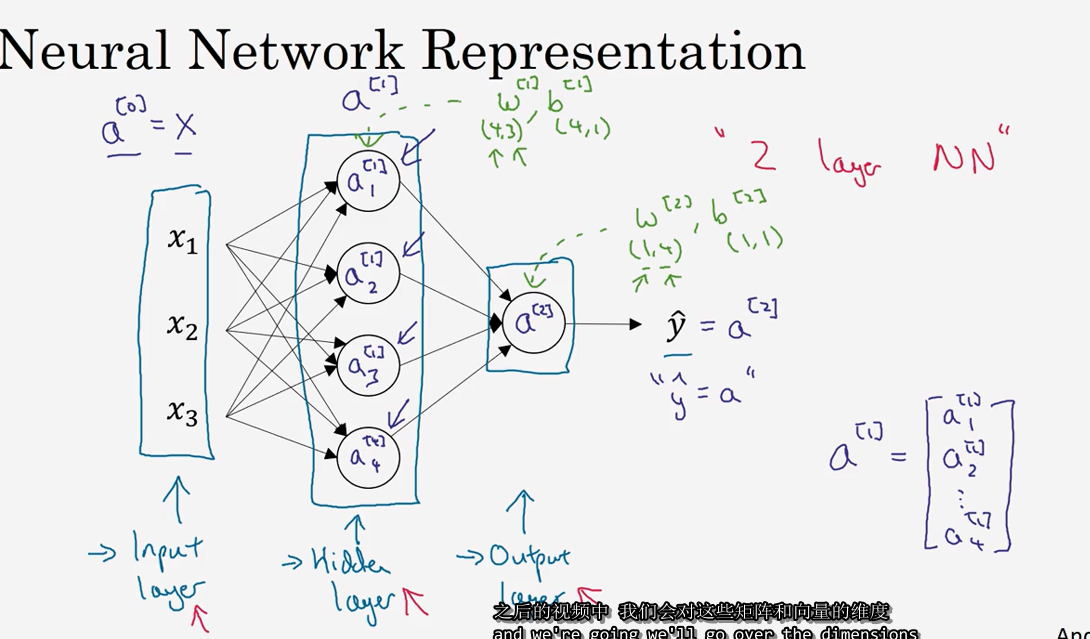


3.3 计算一个神经网络的输出(Computing a Neural Network's output )
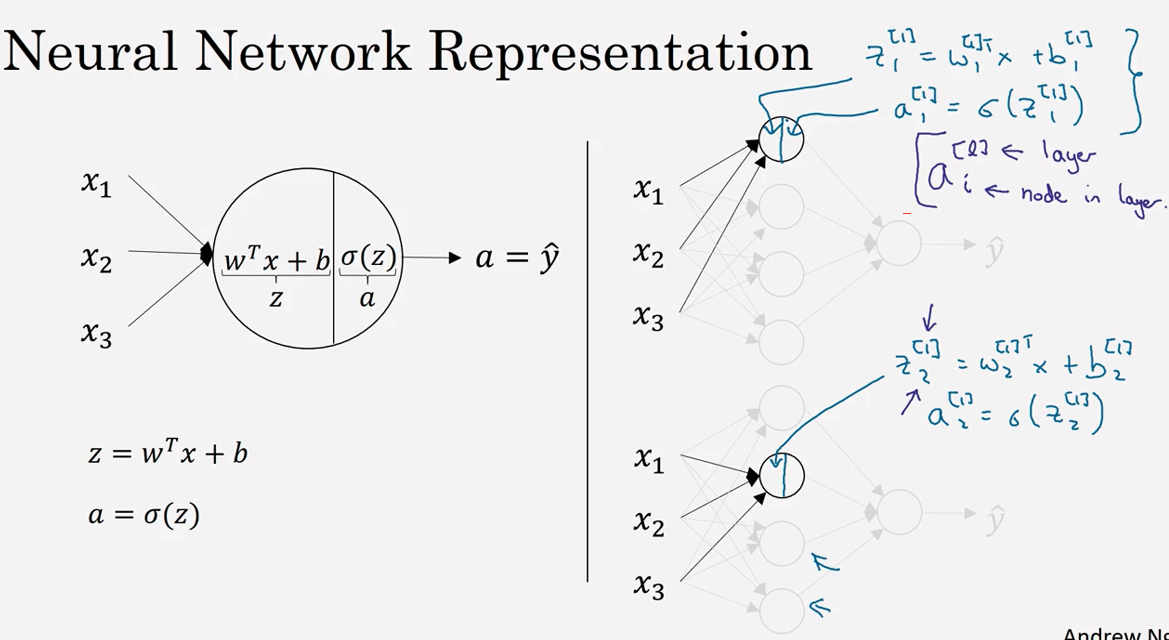

向量化计算:

详细过程见下: 公式 3.10:
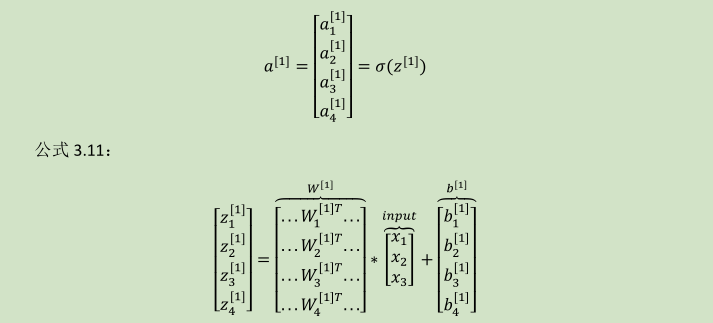
(W---4x3)
3.4 多样本向量化(Vectorizing across multiple examples )

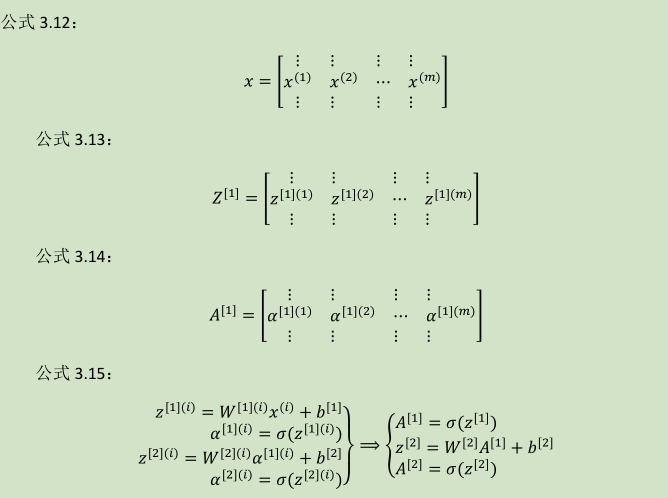
所以横向矩阵A会扫过不同的训练样本,竖向是矩阵A中的不同指标。
3.5 向 量 化 实 现 的 解 释 (Justification for vectorized implementation)
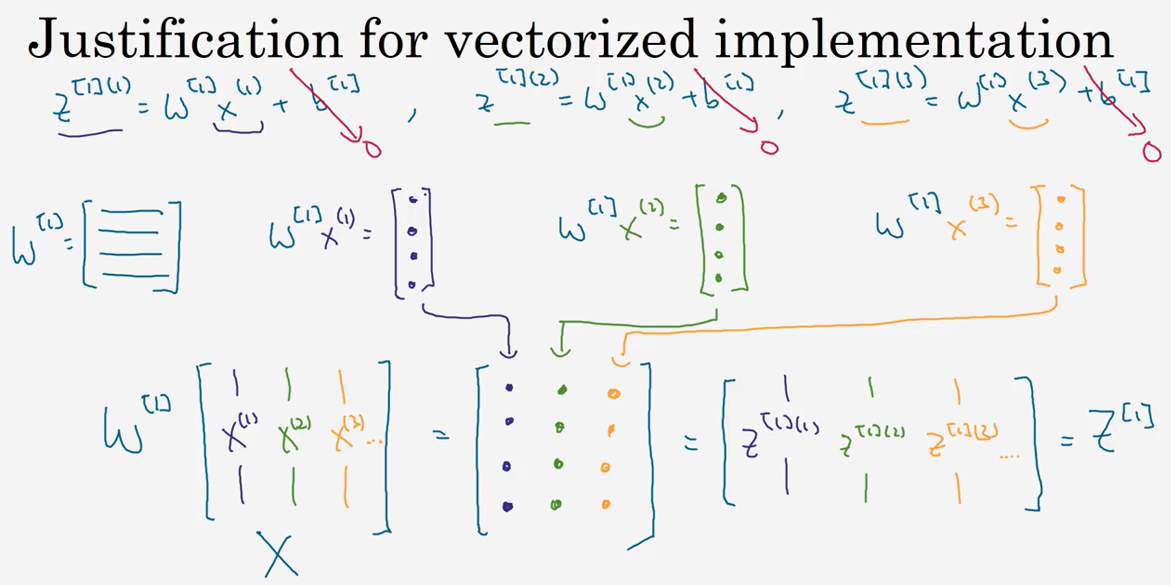

3.6 激活函数 (Activation functions)
-
tanh函数


-
修正线性单元的函数(ReLu)(默认选项!)
-
如果输出是 0、1 值(二分类问题),则输出层选择 sigmoid 函数,然后其它的所有单元都选择 Relu 函数。
-
这是很多激活函数的默认选择,如果在隐藏层上不确定使用哪个激活函数,那么通常会使用 Relu 激活函数。有时,也会使用 tanh 激活函数,但 Relu 的一个缺点是:当z是负值的时候,导数等于 0。
-
这里也有另一个版本的 Relu 被称为 Leaky Relu。当z是负值时,这个函数的值不是等于 0,而是轻微的倾斜,如图。这个函数通常比 Relu 激活函数效果要好,尽管在实际中 Leaky ReLu 使用的并不多。
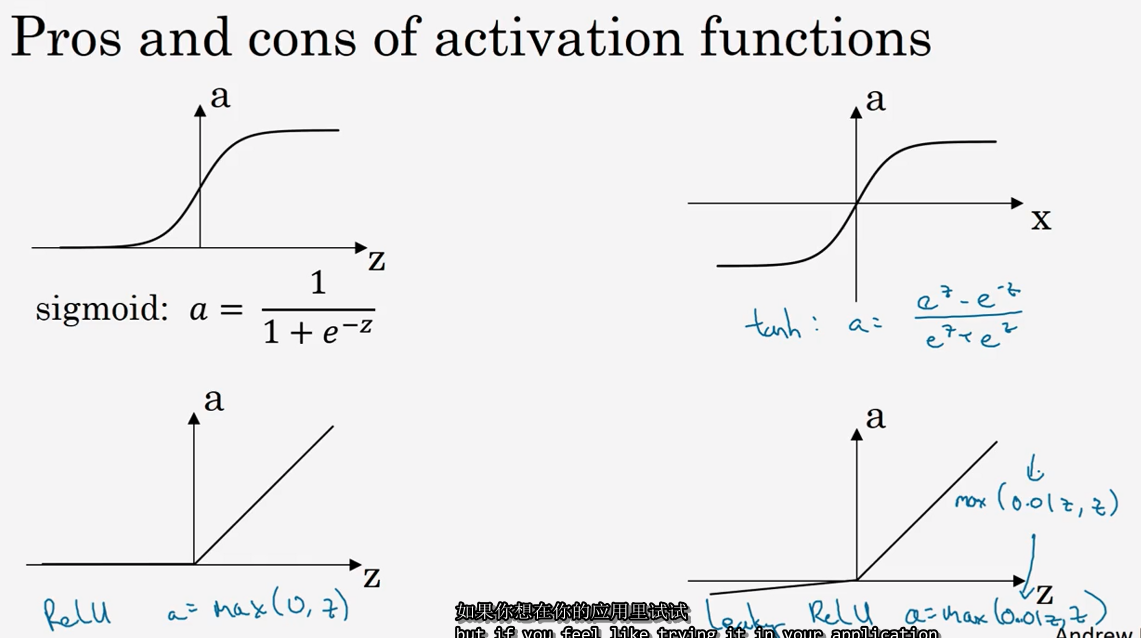
快速概括一下不同激活函数的过程和结论。
- sigmoid 激活函数:除了输出层是一个二分类问题基本不会用它。
- tanh 激活函数:tanh 是非常优秀的,几乎适合所有场合。
- ReLu 激活函数:最常用的默认函数,,如果不确定用哪个激活函数,就使用 ReLu
- Leaky ReLu: 公式 3.23: 𝑏 = max(0.01z, z)
3.8 激活函数的导数 (Derivatives of activation functions)
1) sigmoid activation function

( g' (z) = a(1 - a) )
2) Tanh activation function
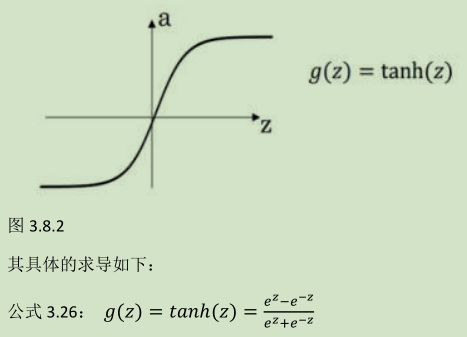
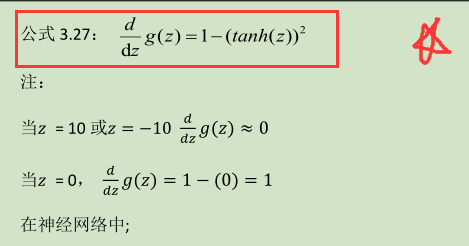
(g ' (z) = 1 - a^2 )
3) Rectified Linear Unit (ReLU)
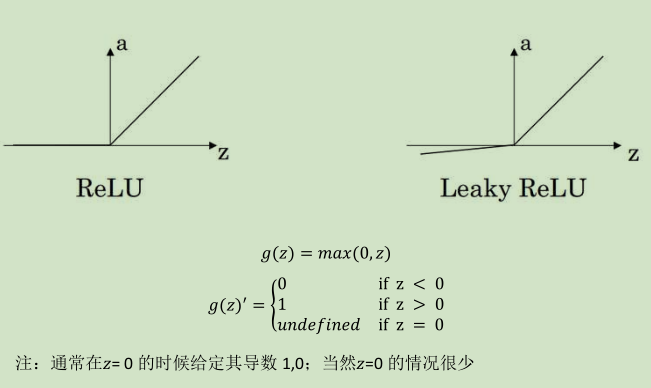
4) Leaky linear unit (Leaky ReLU)

3.9 神经网络的梯度下降 (Gradient descent for neural networks)



3.10 直观理解反向传播 (Backpropagation intuition)





3.11 随机初始化 (Random+Initialization)
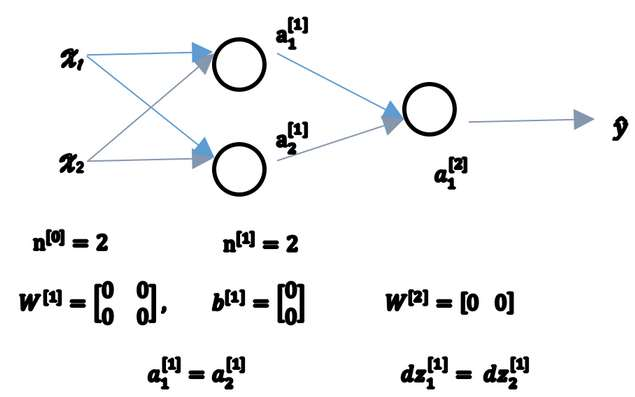
一次迭代后同样的表达式结果仍然是相同的,即隐含单元仍是对称的。通过推导,两次、三次、无论多少次迭代,不管你训练网络多长时间,隐含单元仍然计算的是同样的函数。没有意义。

本周总结
-
如何设立单隐层神经网络
-
随机初始化参数
-
正向传播计算预测值
-
计算导数,结合反向传播应用在梯度下降



