Neural Networks and Deep Learning(week2)神经网络的编程基础 (Basics of Neural Network programming)
总结
一、处理数据
1.1 向量化(vectorization)
- (height, width, 3) ===> 展开shape为(heigh*width*3, m)的向量
1.2 特征归一化(Normalization)
- 一般数据,使用标准化(Standardlization), z(i) = (x(i) - mean) / delta,mean与delta代表X的均值和标准差,最终特征处于【-1,1】区间
- 对于图片,可直接使用 Min-Max Scaliing,即将每个特征直接除以 255,使值处于 【-1,1】之间
二、初始化参数
- 一般将w 和 b随机初始化。这里用逻辑回归思想,设为0
三、梯度下降(Gradient descent)
- 根据w, b和训练集,来训练数据。需要设定迭代次数与learning rate α
3.1 计算代价函数(前向传播)
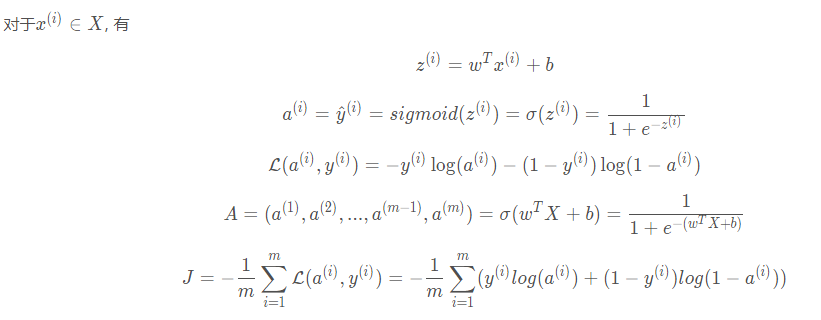
# 激活函数
A = sigmoid(w.T.dot(X) + b)
# 代价函数
cost = -np.sum(Y * np.log(A) + (1-Y) * np.log(1 - A)) / m
3.2 反向传播计算梯度

dw = X.dot((A - Y).T) / m
db = np.sum(A - Y) / m
3.3 更新参数(w, b)
w = w - learning_rate * dw
b = b - learning_rate * db
四、预测测试集
- 用训练好的模型(训练后的参数w, b),对测试集使用 y_hat = sigmoid(wx + b),计算预测结果的概率( np.round(y_hat)))
详细内容
逻辑回归
(1) 逻辑回归的代价函数(Logistic Regression Cost Function )




(2) 梯度下降法(Gradient Descent )
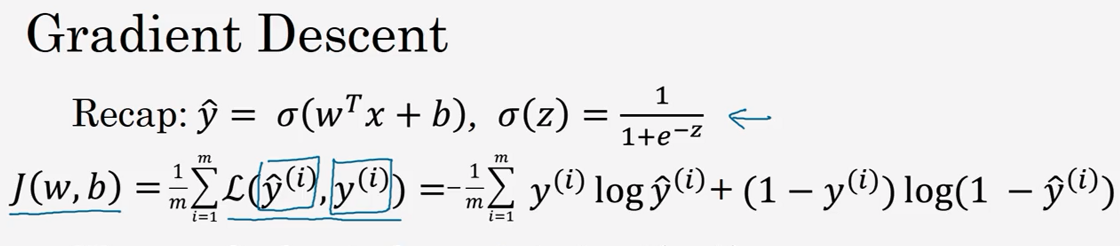
在你测试集上,通过最小化代价函数(成本函数)J(w,b)来训练的参数 w 和 b



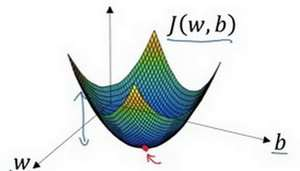

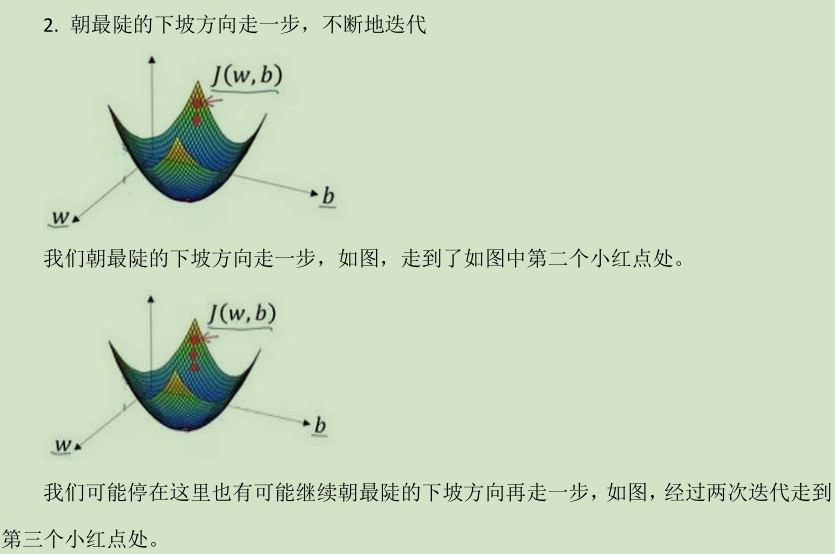

假定代价函数(成本函数)J(𝑥) 只有一个参数w,即用一维曲线代替多维曲线,这样可
以更好画出图像。


2.5 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)





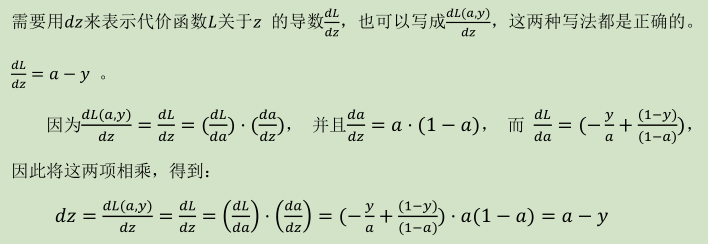
( 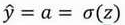 ,
, ![]() )
)

2.6 m 个样本的梯度下降(Gradient Descent on m Examples)

 (应用了一步梯度下降)
(应用了一步梯度下降)
J=0; dw1=0; dw2=0; db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J /= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
上面方法有缺点:(1)两个for循环,算法低效(2)下面将应用向量化来进行
2.7 向量化(Vectorization)

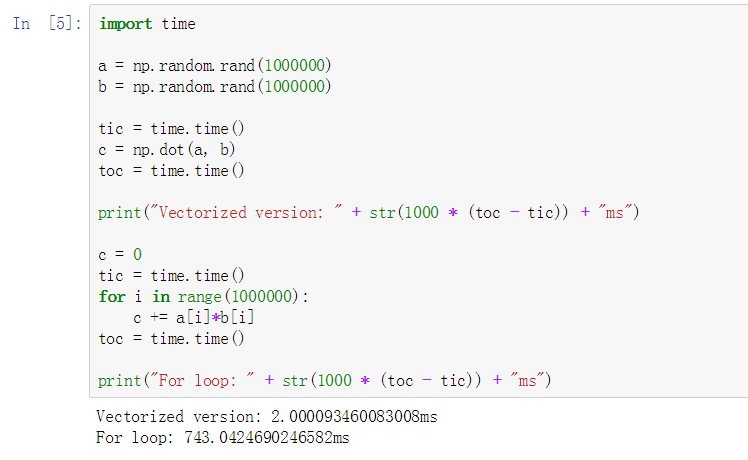
2.8 向量化的更多例子(More Examples of Vectorization



2.9 向量化逻辑回归(Vectorizing Logistic Regression)
-
利用前向传播计算预测值a的过程


$W: (m, 1), X: [x^{(1)}, x^{(2)}, ...x^{(m)}]-(m, n_x), b:(1,1)$
$Z = W^Tx + b-(1, n_x)$
Z = np.dot(w.T, X) + b
A = sigmoid(Z)
2.10 向量化 logistic 回归的梯度输出(Vectorizing Logistic Regression's Gradient )

dw 仍然需要一个循环遍历训练集,我们现在要做的就是将其向量化!

 (
(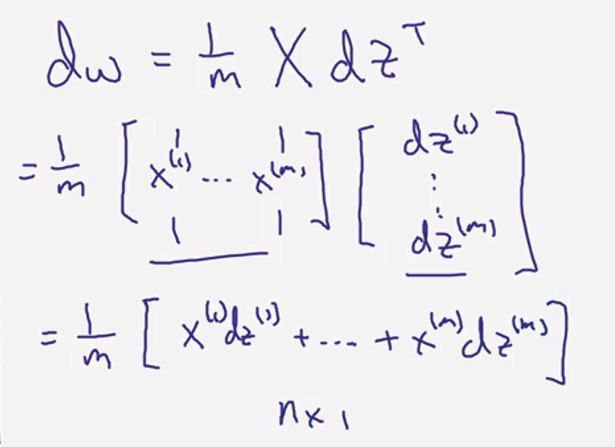 )
)
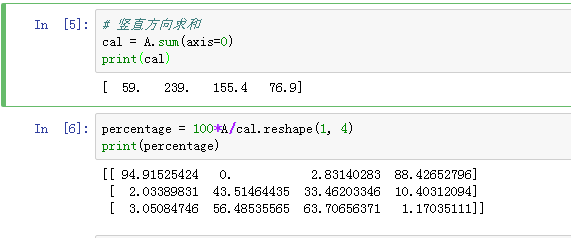
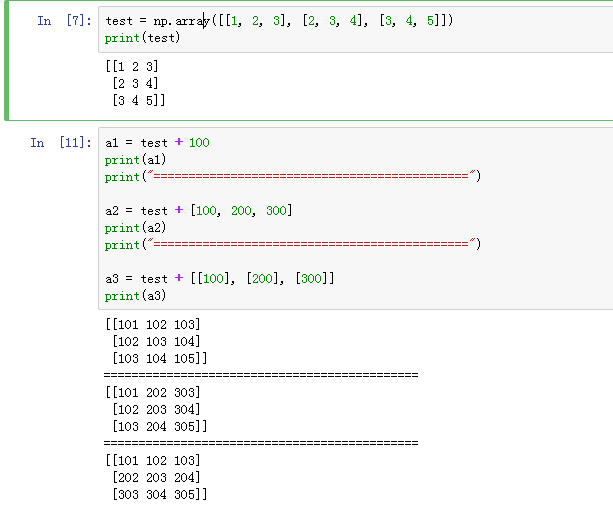
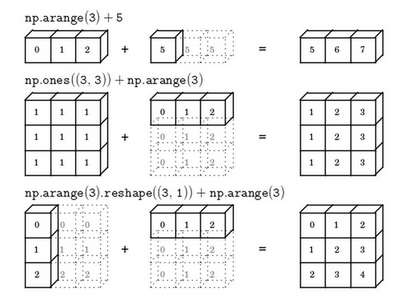
2.11 Python 中的广播(Broadcasting in Python)


2.12 logistic 释 损失函数的解释(Explanation of logistic regression cost function )









