线性代数感悟之4 通过增广矩阵查看解的情况上篇
最近在看 liuyubobobo 的 线性代数 课,感觉很妙,有些感悟记录一下~~~
通过增广矩阵查看解的情况:
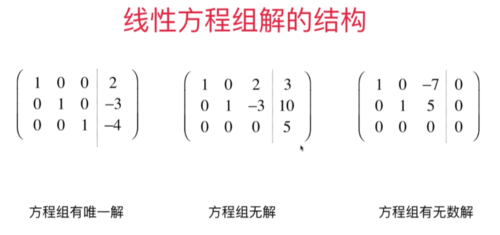
------------------------------------------------------------------------------------------------------------------------------
主元(首元)定义:非零行的第一个元素。
什么是阶梯形矩阵?
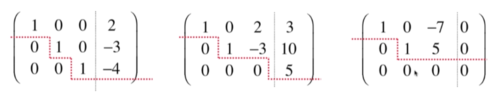
感性定义:可以画个阶梯,阶梯下面都是0
理性定义:
-
有全零行的话,一定是在矩阵的最下方
-
主元的位置,随着行号的递增,向右偏。
-
阶梯下方的元素都是0
如果在阶梯型矩阵的条件下,继续满足一个条件:
4. 主元为1,且主元所在列其他元素为0。
那么 这样的矩阵称之为,rref(行最简形式),

以下两个矩阵,都满足RREF的定义:

分析:
1 首先它是一个阶梯形矩阵
2 主元为1,且主元所在列其他元素为0。
以下矩阵不是行最简形式:
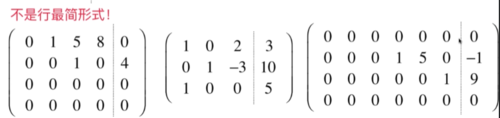
分析:
第一个是阶梯型矩阵,但是不满足:主元为1,且主元所在列其他元素为0。
第二个和第三个,不是阶梯型矩阵。
----------------------------------------------
接下来将增广矩阵变化成行最简形式,再来判断解的的结构。
首先给出定义:
系数矩阵:这个矩阵只包括原方程组的系数,没有等式右侧的那个常数。(及虚线左边的矩阵)
下图中的A就表示 “系数矩阵”,而未知数的个数就是看,系数矩阵有几列。

这里还有个,行最简形式的非零行,就是整个矩阵的非零行。’
由于对比的是系数矩阵和整个矩阵,而系数矩阵是被包含在整个矩阵之内的。
所以非零行的个数,只可能是系数矩阵的个数小于等于整个矩阵的个数(不可能大于)。
那么先看非零行是否一致,不一致的话(不相等),那绝对小于。此时无解。
如果一致,再看是有唯一解还是无数解。
小结:
-
1 最重要的就是系数矩阵的非零行个数
-
2 先对比非零行是否一致,不一致,无解(一致就在往下看)
-
3 再看未知数个数,判断有几个解
3.1 如果 未知数个数=A非零行,那此时,A就是一个单位矩阵了!所以一定是唯一解
3.2 如果 A非零行<未知数个数 此时无数解
3.3 不存在 A非零行>未知数个数 的情况:画一下,就知道了,如果非零行大于列数(及未知数个数),那就不满足阶梯矩阵了!
作者:宋桓公
出处:http://www.cnblogs.com/douzi2/
如果您觉得阅读本文对您有帮助,请点一下“推荐”按钮,您的“推荐”将是我最大的写作动力!欢迎各位转载,但是未经作者本人同意,转载文章之后必须在文章页面明显位置给出作者和原文连接,否则保留追究法律责任的权利。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现
2015-04-27 论FPGA建模,与面向对象编程的相似性