【详解】为何三元一次方程可以表示一个平面

首先如何确定一个平面？

1 知道平面的倾向角（比如知道一个平面与某个向量垂直）

2 知道整个平面过某个点

这样整个平面就被确定下来。

当 Ax+By+Cz=0

对于这个方程来说，也就是向量（A,B,C）与（x,y,z）垂直。

（x,y,z）可以表示空间中某个点，那么，假设有个平面，与（A,B,C）垂直，

这个平面恰好经过了点(x y z). 那么这个平面及与（A,B,C）垂直，且经过了一个点。

说明这个平面被确定下来

反过来说，这个平面上的所有的点，构成的平面与（A,B,C）垂直。

给出图片进行进一步说明：

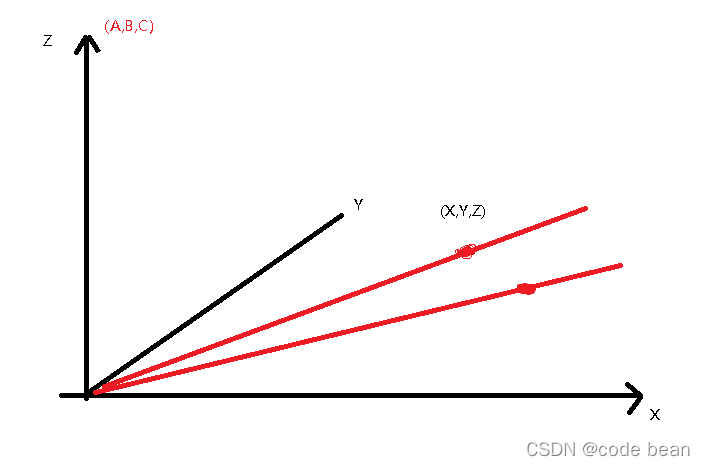
假设 向量（A,B,C）就是Z轴，（x,y,z）这个点就在X轴和Y轴构成的平面上。

那么在这个平面上的所有的点构成的向量（单点构成向量，另一个点就是原点）都与（A,B,C）

垂直。

进一步分析，如果（A,B,C）就是Z轴，那说明A和B就是0。且C不是0， 那

Ax+By+Cz=0 就是，Cz = 0；（所以xy没有任何的限制）

由于Cz = 0； 而C不为0，所以z必须为零。此时x,y又没有任何的限制。那这个平面在哪，就不言而喻了。

所以，只要ABC定下来，xyz的关系就定下来了，那么这个平面就定下来了。所以说，三元一次方程可以表示一个平面。

---

当Ax+By+Cz=D，分解一下就可以变成，A(x-x0)+B(y-y0)+C(z-z0)=0

也就是向量（A,B,C）与（x-x0, y-y0, z-z0）垂直。

证明过程和上方一致。