卷积神经网络CNN中的卷积操作详解

从公式理解：

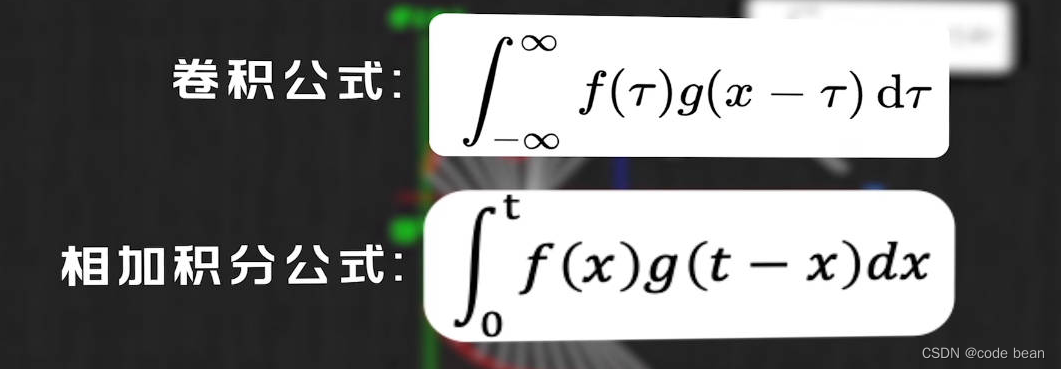
从公式看，卷积就是相乘再相加的过程

从这张图看，卷积就是之前的点对当前点的影响。有人说，卷积就是瞬时行为的持续性后果。

CNN中的卷积操作

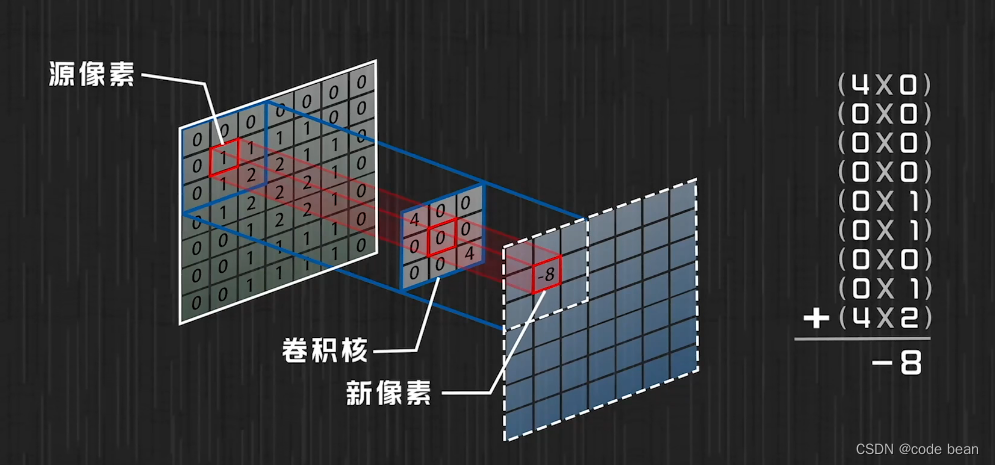
在CNN的卷积操作中，其实也是先相乘再相加，这里通过卷积核，实现一个目的，就是周围像素点对中心像素点的影响。

那不同的卷积核，对图像的影响是不同的：

去噪：

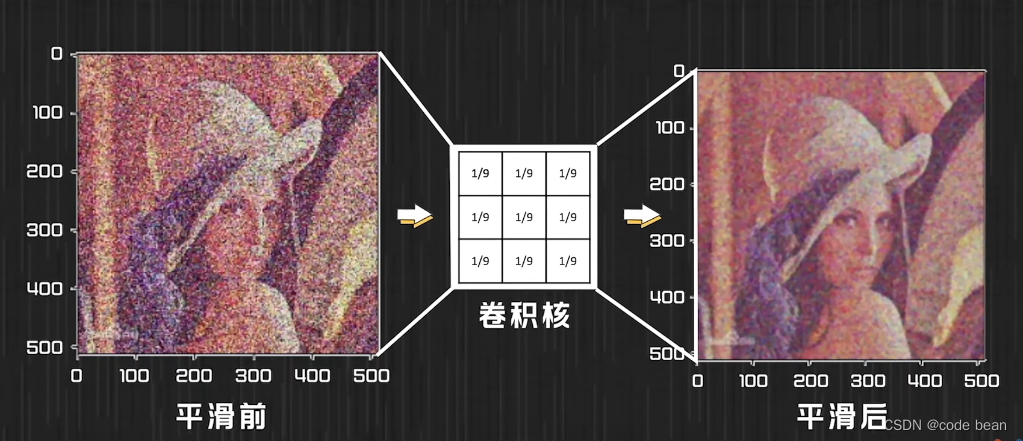
挑出，垂直边界货水平边界

那有人，可能会问了，那想提取某个特殊的特征，这个卷积核怎么去设置呢？那其实这个卷积核的值可以先随便预设一个，然后训练后通过反向传播进行优化。

也就是说，我们可以通过不同的卷积核挑出来不同特征,然后再将这些特征作为全连接层的输入。特征本身的个数也可以预设，特征的个数和卷积核的个数相等。

这里我也就发现了卷积的主要目的了：

一开始我们的对象是成千上万的像素，如果我们一开始就使用全连接层，比如我们现在有4563个像素，那将构建如下图的全连接层：

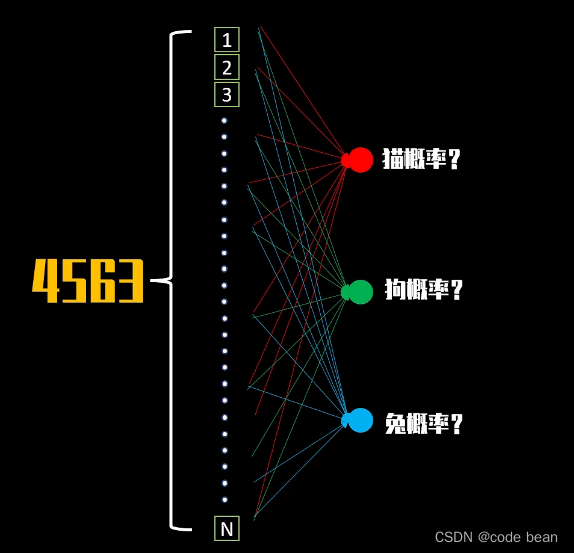
这样就会有太多的w和b需要调整，增加训练的难度，所以我们先需要通过卷积提取特征，过滤无关紧要的信息，然后再通过全连接层，输出概率。

卷积层

那现在看下这个卷积层的运行过程：

那或者过程就是将卷积核盖到原图上，做相乘再相加的操作，每完成一次这样的操作就平移一次。那图中将原图扩充了一圈，这个骚操作叫做Padding，作用如上图中文字所述。

再平移的时候，还有个骚操作，“一次平移多个格子”，到达缩小图片的作用。

这个就是步幅，和接下来的要讲的池化有着类似的功效。

池化层

在一般卷积神经网络中，卷积层后面紧接着跟着一个池化层：

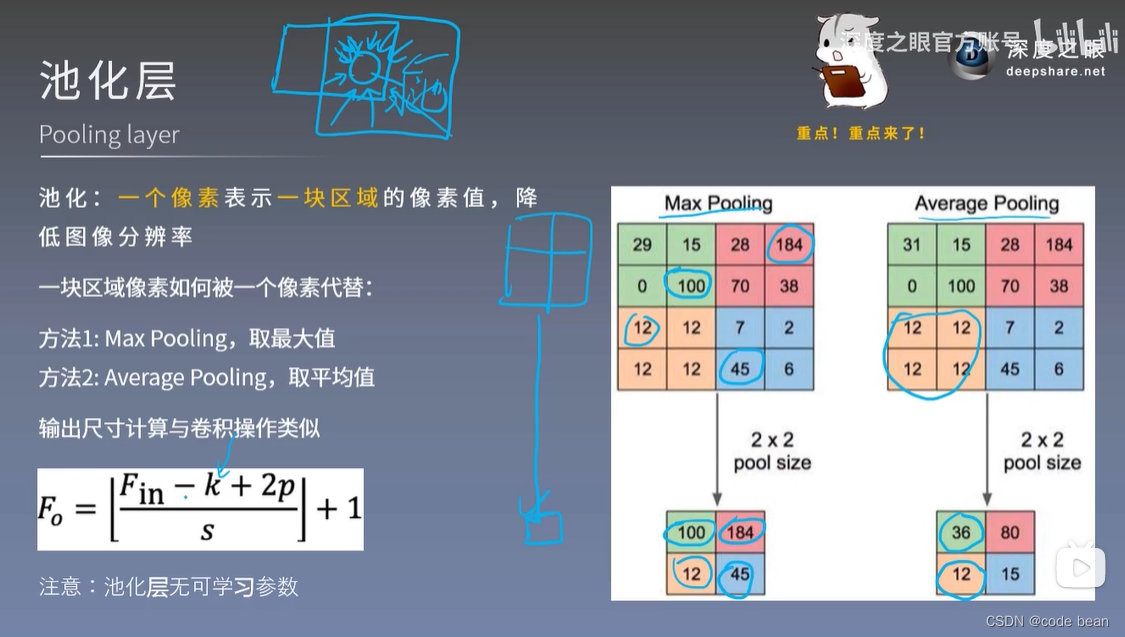
具体作用，请参考上图。

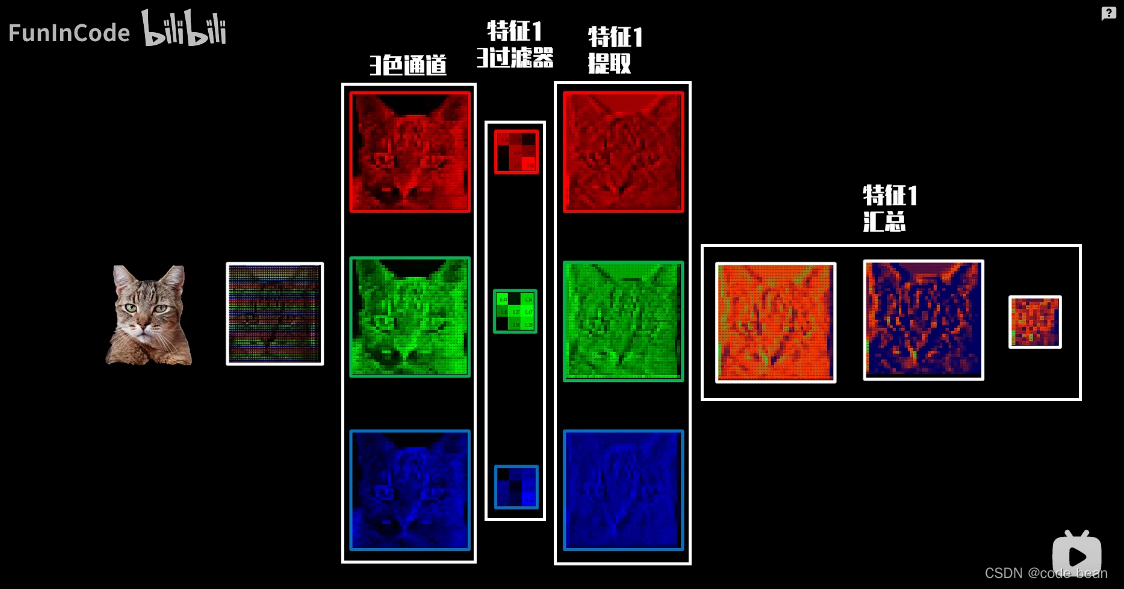
现在从整体的角度看一看：

上图中，虽然写了三个卷积核，但是其实是一个卷积核的三个通道（RGB），这里要十分注意，

卷积核的个数和特征种类是一一对应的，而不是图片的通道数。

从下图就能看出，三个通道的的特征最后要汇总，还是归为一个特征。这个卷积核的维度问题，我放到最后讲解。

扁平化处理

池化之后得到的是一个较小特征矩阵，在这个矩阵中包含的是一个特征的所有数据，为了后续计算的方便，会进行一个扁平化的处理：

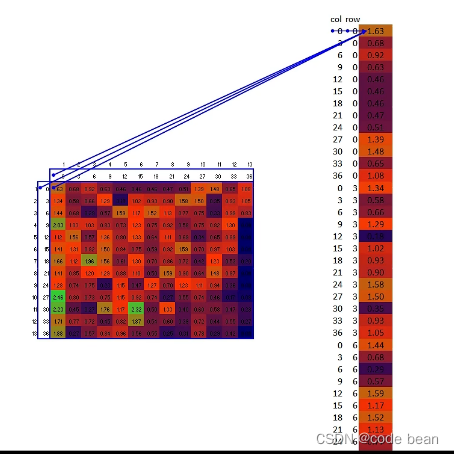
上图中池化后的矩阵为13*13=169，扁平化之后的一条数据就169个数据。

因为，上图中只有一个卷积核，所以只有一种特征，那如果有两种特征，扁平化因该看到的是这种效果：

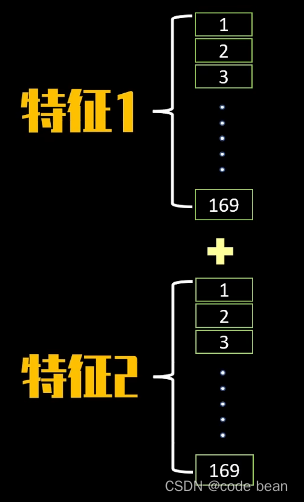
卷积核的维度问题

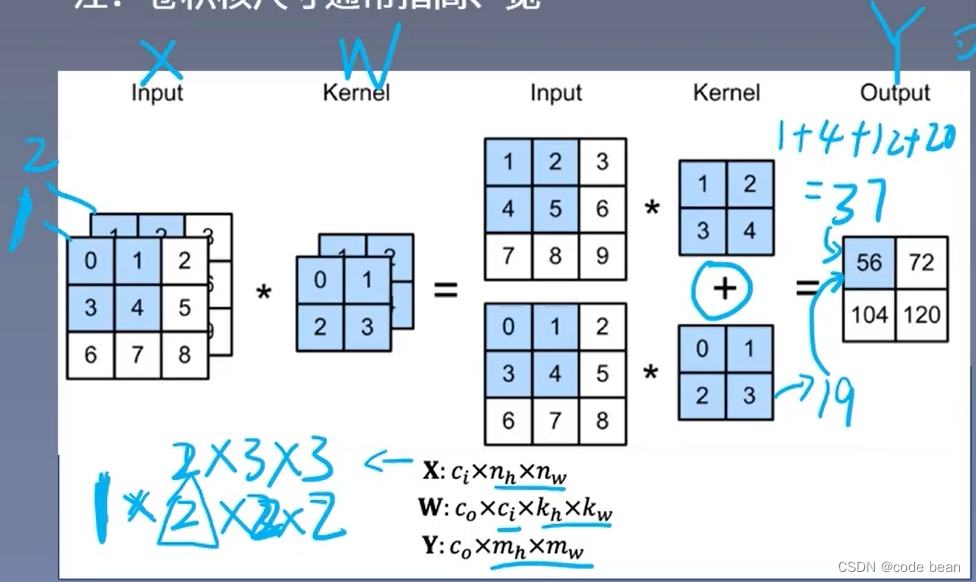
1 X作图片为输入，看成一个三维的数据。Ci表示通道数（如：RGB），这个和卷积核的Ci是必须相等的。后面两个是图片的宽和高.

2 W就是卷积核它一个是四维，C0表示的是特征的个数，也是卷积核的个数，Ci上面说了是通道数。后面两个是图片的宽和高。

3 Y就是特征采集部分的输出，你会发现Ci不见了，那是因为不管你图像是几个通道，最终都会相加进行特征汇总，而变成一维。而C0就是特征种类和W的第一个维度相同。后面两个是图片的宽和高。

下面就看一个两种特征的情况（两个卷积核的例子）：

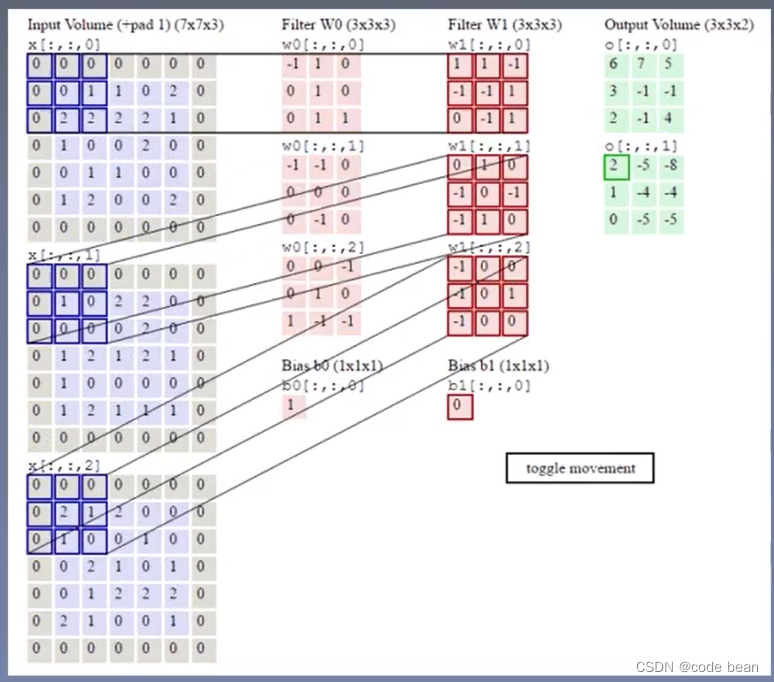
W0 和W1就分别是两个卷积核（图种，把卷积核的偏置项b也画出来了），最终就得到了两种特征输出。

再来一张图，说明的是同样的意思：可以清楚的看到数据从n维到m维的变化：

通过程序构建卷积层

1 首先我们构建图片输入数据

import torch
# channels，通道数
in_channels, out_channels= 3, 10
# 图片的宽高
width, height = 60, 60
# 卷积核大小3*3
kernel_size = 3
# 一个batch中样本的个数 
batch_size = 7
# 构建输入
input = torch.randn(batch_size,in_channels,width, height)

torch.randn 表示数据本身的值都符合正态分布。最终得到的input是一个四维的张量：

torch.Size([7, 3, 60, 60])

2 构建卷积层操作

torch.nn.Conv2d 用于构建卷积层操作，你可以设置数据到了这一层之后如何进行卷积

比如设置stride和padding

stride：卷积每次滑动的步长为多少，默认是 1
padding：设置在所有边界增加值为 0 的边距的大小（也就是在feature map 外围增加几圈 0 ）

当前我们最重要的是告诉Conv2d，输入多少，输出多少，以及卷积核的大小

conv_layer = torch.nn.Conv2d(in_channels,out_channels,
                             kernel_size=kernel_size,
                             padding=1,
                             stride=2                             
                            )

此时Conv2d 就已经帮我们构建了卷积层，那么来看看conv_layer.weight的形状：

torch.Size([10, 3, 3, 3])

10表示的是10个卷积核，对应out_channels是通道的输出。
第一个3，对应的是图像的通道数in_channels
最后两个3就是卷积核的大小3*3

3 最后看下输出

这一步就是使用卷积层对输入信号做卷积计算，output为卷积后的输出：

output = conv_layer(input)

那看一下为啥是：[7, 10, 30, 30]

7是batch_size这个不会变，进来七张图片，出来还是7张。

10是out_channels，这个是我们卷积层规定的。

30*30是卷积后得到特征图片的大小：

因为kernel_size=3 且padding=1表示卷积后图片大小不变，但是stride步幅设置成了2，所以图片由60*60变到了30*30

到处，我们的代码和分析得到完全一致的结果。

实战部分

接下来我们来自己构建一个卷积神经网络，其结构如下图：

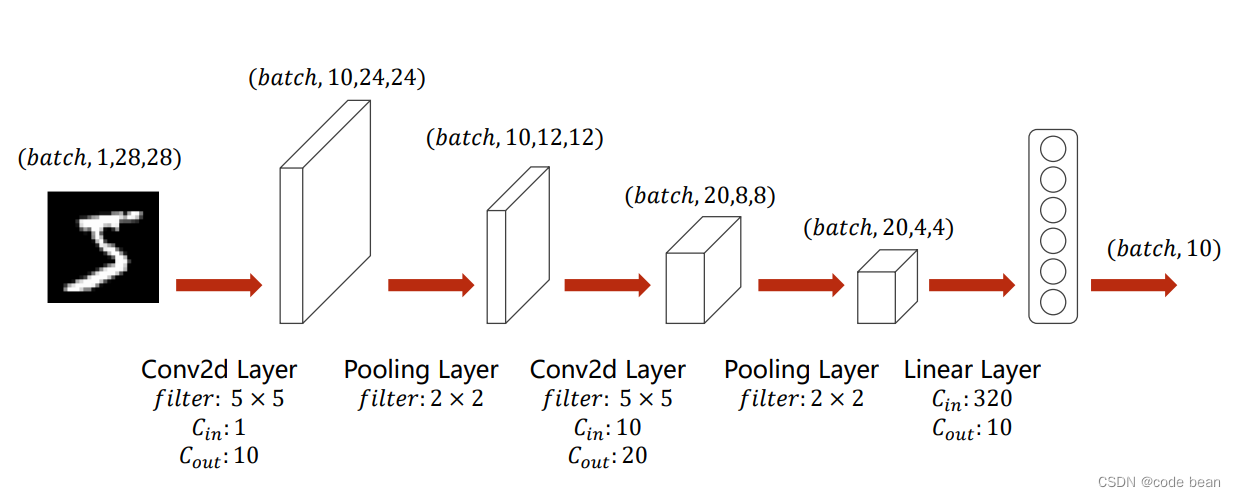
那其实，我们只要将上面文章中的最后的例子的模型替换一下：pytorch 多分类中的损失函数_code bean的博客-CSDN博客https://blog.csdn.net/songhuangong123/article/details/125502262?spm=1001.2014.3001.5501

上篇例子中，直接用的全连接的神经网络，训练后准确率达到97%止步，这次看看换成卷积神经网络，会怎样？

将模型替换为：

# 换成这个网络就OK了
class Net2(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320, 10)

    def forward(self, x):
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size, -1)  # flatten
        # 最后一层不进行激活，不做非线性变换
        x = self.fc(x)
        return x

这段代码和上图是一一对应的，先卷积再池化先卷积再池化，最后通过view函数进行扁平化处理。

这里说明几个问题：

1 torch.nn.Linear(320, 10) 为啥这里的全连接的输入是320？

因为卷积到最后变成了(batch_size,20，20，4), 20*20*4就是320，那最后输出的点数是320*batch_size

batch_size是图片的数量，他的每个子元素就是一张图片，所以扁平化的时候，还是要固定一个维度的，那就是batch_size: x = x.view(batch_size, -1)

最后将这个x给： torch.nn.Linear(320, 10)，最后强调一下就是pytorch里的函数都是处理矩阵的函数，所以batch_size这个维度是不能丢掉的，就像之前我们定义输入数据那样，这里必须是二维的：

# 注意这里必须写成两维的矩阵
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])

2 最后一层不进行激活，不做非线性变换

因为我们选择了交叉熵那个损失函数，里面有个softmax做了非线性变化。

最后还是上完整的代码：

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.optim as optim
import torch.nn.functional as F

# 准备数据集
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])

train_dataset = datasets.MNIST(root='./dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='./dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)


# 构造网络模型
class Net(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        # 将C*W*H三维张量变为二维张量，用于深度深度学习处理
        x = x.view(-1, 784)
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        # 最后一层不进行激活，不做非线性变换
        return self.l5(x)


# 换成这个网络就OK了
class Net2(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320, 10)

    def forward(self, x):
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size, -1)  # flatten
        # 最后一层不进行激活，不做非线性变换
        x = self.fc(x)
        return x


model = Net2()

# 构造损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()  # 此函数，需要一个未激活的输入，它将 交叉熵 和 softmax 的计算进行融合。（这样计算更快更稳定！）
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # momentum：冲量


def train(epoch):
    running_loss = 0
    for batch_idx, data in enumerate(train_loader, 0):
        # 获得一个批次的输入与标签
        inputs, target = data
        # 开始训练
        optimizer.zero_grad()
        # 正向传播
        y_pred = model(inputs)
        # 计算损失
        loss = criterion(y_pred, target)
        # 反向传播
        loss.backward()
        # 更新梯度
        optimizer.step()

        running_loss = running_loss + loss
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0


def my_test():
    correct = 0
    total = 0
    # 不计算梯度
    with torch.no_grad():
        for data in test_loader:
            inputs, labels = data
            prec = model(inputs)
            '''
            torch.max(input, dim) 函数
            输入:
            input是softmax函数输出的一个tensor
            dim是max函数索引的维度0/1，0是每列的最大值，1是每行的最大值
            输出:
            函数会返回两个tensor，第一个tensor是每行的最大值，softmax的输出中最大的是1，
            所以第一个tensor是全1的tensor；第二个tensor是每行最大值的索引,这个索引的值正好和预测的数字相等。
            '''
            _, predicted = torch.max(prec.data, dim=1)  # predicated为维度（784，1）的张量
            total += labels.size(0)
            # 张量之间的比较运算
            correct += (predicted == labels).sum().item()
    print('accuracy on test set: %d %% ' % (100 * correct / total))


if __name__ == "__main__":
    for epoch in range(10):  # 每轮训练之后，都预测一次
        train(epoch)
        my_test()

[1,   300] loss: 0.689
[1,   600] loss: 0.214
[1,   900] loss: 0.135
accuracy on test set: 96 % 
[2,   300] loss: 0.115
[2,   600] loss: 0.105
[2,   900] loss: 0.084
accuracy on test set: 97 % 
[3,   300] loss: 0.081
[3,   600] loss: 0.080
[3,   900] loss: 0.065
accuracy on test set: 98 % 
[4,   300] loss: 0.069
[4,   600] loss: 0.061
[4,   900] loss: 0.059
accuracy on test set: 98 % 
[5,   300] loss: 0.057
[5,   600] loss: 0.050
[5,   900] loss: 0.055
accuracy on test set: 98 % 
[6,   300] loss: 0.050
[6,   600] loss: 0.048
[6,   900] loss: 0.048
accuracy on test set: 98 % 
[7,   300] loss: 0.046
[7,   600] loss: 0.045
[7,   900] loss: 0.043
accuracy on test set: 98 % 
[8,   300] loss: 0.038
[8,   600] loss: 0.045
[8,   900] loss: 0.039
accuracy on test set: 98 % 
[9,   300] loss: 0.040
[9,   600] loss: 0.039
[9,   900] loss: 0.035
accuracy on test set: 98 % 
[10,   300] loss: 0.037
[10,   600] loss: 0.035
[10,   900] loss: 0.035
accuracy on test set: 98 %

非常好，准确率上升1%

Lenet

最后从第一个商用的神经网络卷积模型来整体看一看：

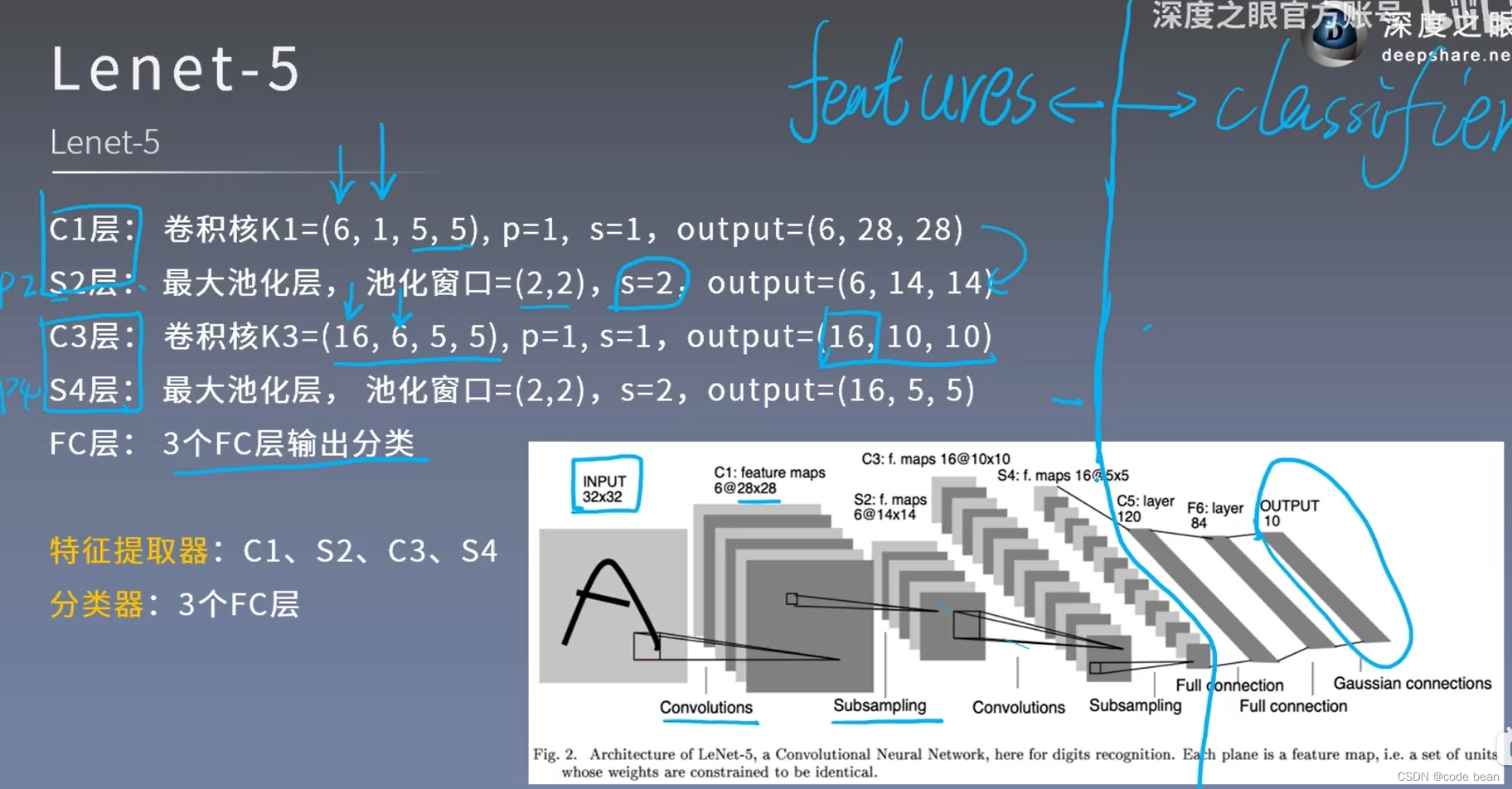
图中蓝色线左侧，为特征提取部分，包含了卷积和池化，右边就是全连接层，进行分类。

感觉和我们构建的也差不多~~~

参考资料中的视频都是非常经典的（第二个可以不看），可以反复观看。

参考资料：

【视频课件资料见置顶评论】深度学习入门必学丨神经网络基础丨卷积神经网络丨循环神经网络_哔哩哔哩_bilibili

卷积究竟卷了啥？——17分钟了解什么是卷积_哔哩哔哩_bilibili

从“卷积”、到“图像卷积操作”、再到“卷积神经网络”，“卷积”意义的3次改变_哔哩哔哩_bilibili

【数之道 31】使用Excel深度剖析卷积神经网络模型，12分钟理解全部知识点_哔哩哔哩_bilibili

posted @ 2022-06-30 17:32 宋桓公阅读(418) 评论(0) 编辑收藏举报

刷新页面返回顶部

宋桓公

勇于尝试，才有突破。选择是一种乐趣，期待产生的结果～～欢迎关注我的哔哩哔哩账号：
code_bean(猛戳)
这里将以视频的形式展示，文本+视频，让知识点更好掌握

卷积神经网络CNN中的卷积操作详解

从公式理解：

CNN中的卷积操作

卷积层

池化层

扁平化处理

卷积核的维度问题

通过程序构建卷积层

1 首先我们构建图片输入数据

2 构建卷积层操作

3 最后看下输出

实战部分

Lenet

公告

宋桓公

勇于尝试，才有突破。选择是一种乐趣，期待产生的结果～～ 欢迎关注我的哔哩哔哩账号：code_bean(猛戳) 这里将以视频的形式展示，文本+视频，让知识点更好掌握

卷积神经网络CNN中的卷积操作详解

从公式理解：

CNN中的卷积操作

卷积层

池化层

扁平化处理

卷积核的维度问题

通过程序构建卷积层

1 首先我们构建图片输入数据

2 构建卷积层操作

3 最后看下输出

实战部分

Lenet

公告

勇于尝试，才有突破。选择是一种乐趣，期待产生的结果～～欢迎关注我的哔哩哔哩账号：
code_bean(猛戳)
这里将以视频的形式展示，文本+视频，让知识点更好掌握