本篇不想写什么了,后续想到什么再更上吧。
注:本代码二叉树的构建是按照二叉排序树来构建的。后续的测试等都用到此二叉树。
代码大部分来源于《数据结构考研复习指导》,即王道单科。
层次遍历:
求某一层的结点个数,树的高度,每一层结点个数,树的最大宽度
中序遍历:
判断是否二叉排序树
后序遍历:
判断是否平衡二叉树,树的高度,
#include<stdio.h> #include<stdio.h> #include<malloc.h> #define ElemType int #define maxSize 500 typedef struct BiTNode{ ElemType data; struct BiTNode *lchild,*rchild; }BiTNode,*BiTree; //构建二叉排序树,通过逐个插入法 int BST_Insert(BiTree &T,ElemType k){ //注意T前面要有引用&。 if(T==NULL){ T=(BiTree)malloc(sizeof(BiTNode)); T->data=k; T->lchild=T->rchild=NULL; return 1; } else if(T->data==k)return 0; else if(k<T->data) return BST_Insert(T->lchild,k); else return BST_Insert(T->rchild,k); } int BST_Create(BiTree &T,ElemType a[],int n){ T=NULL; for(int i=0;i<n;i++){ BST_Insert(T,a[i]); } } //遍历时首先都应该看是不是空树 //前序遍历 int PreOrder(BiTree T){ if(T!=NULL){ printf("%d ",T->data); PreOrder(T->lchild); PreOrder(T->rchild); } } //中序遍历 int InOrder(BiTree T){ if(T!=NULL){ InOrder(T->lchild); printf("%d ",T->data); InOrder(T->rchild); } } //后序遍历 int PostOrder(BiTree T){ if(T!=NULL){ PostOrder(T->lchild); PostOrder(T->rchild); printf("%d ",T->data); } } //前序遍历非递归 void PreOrder2(BiTree T){ if(T!=NULL){ BiTree stack[maxSize]; int top=-1; BiTree p; stack[++top]=T; while(top!=-1){ p=stack[top--]; printf("%d ",p->data); if(p->rchild!=NULL)stack[++top]=p->rchild; //注意先是右孩子入栈,再是左孩子 if(p->lchild!=NULL) stack[++top]=p->lchild; } } } //中序遍历非递归 void InOrder2(BiTree T){ if(T!=NULL){ BiTree stack[maxSize]; int top=-1; BiTree p=T; //后续中序遍历的循环要用到p!=NULL,初始p在跟的位置,下面的程序得以进入循环 while(top!=-1||p!=NULL){//因为中序遍历左子树遍历完后栈空,单 while(p!=NULL){ //中序遍历总是要去到左子树的最左边。 但同时还要回去以前的状态,因此入栈操作也少不了 stack[++top]=p; p=p->lchild; } if(top!=-1){ //栈不空则出栈,每次出栈时养成习惯检查一下栈空不空,除非真的确定,如先序和后序就没检查。 p=stack[top--]; printf("%d ",p->data); p=p->rchild; } } } } //本质和上面那个算法差不多,只不过比较好记。 void InOrder3(BiTree T){ if(T!=NULL){ BiTree stack[maxSize]; int top=-1; BiTree p=T; while(p!=NULL||top!=-1){ if(p){ stack[++top]=p; p=p->lchild; } else{ p=stack[top--]; printf("%d ",p->data); p=p->rchild; } } } } //后序遍历非递归 ,用两个栈。源代码《数据结构高分笔记》可有 void PostOrder2(BiTree T){ if(T!=NULL){ BiTree stack1[maxSize]; BiTree stack2[maxSize]; int top1=-1,top2=-1; BiTree p; stack1[++top1]=T; while(top1!=-1){ p=stack1[top1--]; stack2[++top2]=p; if(p->lchild!=NULL)stack1[++top1]=p->lchild; if(p->rchild!=NULL)stack1[++top1]=p->rchild; //注意看是哪个栈啊。别搞糊涂了。 } while(top2!=-1){ p=stack2[top2--]; printf("%d ",p->data); } } } //后序遍历非递归,用一个栈 。因为是先访问左子树,再访问右子树,最 //后访问根节点,所以用堆栈来存储结点,必须分清返回根节点时,是从左子 //树还是右子树返回的,此处用r指向被访问过的结点。 void PostOrder3(BiTree T){ if(T!=NULL){ BiTree stack[maxSize]; int top=-1; BiTree p=T; BiTree r=NULL; while(p!=NULL||top!=-1){ if(p){ //压入栈,到最左边 stack[++top]=p; p=p->lchild; } else{ p=stack[top]; //取栈顶结点,这句很容易忘!!!!!!!!!! if(p->rchild!=NULL&&p->rchild!=r){ //右子树不为空且还没有访问过 ,转向右,压入栈,继续到最左边 p=p->rchild; stack[++top]=p; p=p->lchild; } else{ p=stack[top--]; printf("%d ",p->data); r=p; p=NULL; } } } } } //层次遍历 void LevelOrder(BiTree T){ if(T!=NULL){ BiTree Q[maxSize]; int front=-1,rear=-1; BiTree p; Q[++rear]=T; while(front<rear){ p=Q[++front]; printf("%d ",p->data); if(p->lchild!=NULL) Q[++rear]=p->lchild; if(p->rchild!=NULL) Q[++rear]=p->rchild; } } } //自下而上,从右到左的层次遍历算法 void LevelOrderReverse(BiTree T){ if(T!=NULL){ BiTree Q[maxSize]; BiTree stack[maxSize]; int front=-1,rear=-1; int top=-1; BiTree p; Q[++rear]=T; while(front<rear){ p=Q[++front]; stack[++top]=p; if(p->lchild!=NULL) Q[++rear]=p->lchild; if(p->rchild!=NULL) Q[++rear]=p->rchild; } while(top!=-1){ p=stack[top--]; printf("%d ",p->data); } } } //递归求二叉树的高度 int Height(BiTree T){ if(!T)return 0; int h1=Height(T->lchild); int h2=Height(T->rchild); return (h1>h2?h1:h2)+1; } //非递归求二叉树的高度,用层次遍历 int Height1(BiTree T){ if(T!=NULL){ BiTree Q[maxSize]; int front=-1,rear=-1; int level=0,last=0; //last=0是因为第一个元素入队后,front的值为0; BiTree p; Q[++rear]=T; while(front<rear){ p=Q[++front]; if(p->lchild!=NULL) Q[++rear]=p->lchild; if(p->rchild!=NULL) Q[++rear]=p->rchild; if(front==last){ //出队元素如果是最后一个元素,层次+1,且更新last指向下一层的最后一个元素。 level++; last=rear; //last指向下一层的最后一个结点。 } } return level; } } //双分支结点数 (递归) int TwoBranchNum(BiTree T){ int n=0; //此处把n的初值设为0非常重要。!!! if(!T)return 0; if(T->lchild!=NULL&&T->rchild!=NULL)n=1; int num1=TwoBranchNum(T->lchild); int num2=TwoBranchNum(T->rchild); return num1+num2+n; } //失败了。 //int twonum=0; //void TwoBranchNum1(BiTree T){ // if(!T) twonum=0; // if(T->lchild!=NULL&&T->rchild!=NULL)twonum++; // TwoBranchNum1(T->lchild); // TwoBranchNum1(T->rchild); //} int TwoBranchNum2(BiTree T){ if(!T)return 0; if(T->lchild!=NULL&&T->rchild!=NULL) return TwoBranchNum2(T->lchild)+TwoBranchNum2(T->rchild)+1; else return TwoBranchNum2(T->lchild)+TwoBranchNum2(T->rchild); } //双分支结点数 ,用层次遍历,这种算法有点无聊。。。。 int TwoBranchNum3(BiTree T){ if(T!=NULL){ BiTree Q[maxSize]; int front=-1,rear=-1; BiTree p; int num=0; Q[++rear]=T; while(front<rear){ p=Q[++front]; if(p->lchild&&p->rchild)num++; if(p->lchild!=NULL) Q[++rear]=p->lchild; if(p->rchild!=NULL) Q[++rear]=p->rchild; } return num; } } //单分支结点数 (递归) int OneBranchNum(BiTree T){ int n=0; //此处把n的初值设为0非常重要。!!! if(!T)return 0; if(T->lchild!=NULL&&T->rchild==NULL)n=1; if(T->lchild==NULL&&T->rchild!=NULL)n=1; int num1=OneBranchNum(T->lchild); int num2=OneBranchNum(T->rchild); return num1+num2+n; } int isCompleted(BiTree T){ if(!T)return 1; BiTree Q[maxSize]; int front=-1,rear=-1; BiTree p; Q[++rear]=T; while(front<rear){ p=Q[++front]; if(p){ //结点非空,左右子树的都入队,空结点也要。 Q[++rear]=p->lchild; Q[++rear]=p->rchild; } else{ while(front<rear){ //只要出现空结点,则循环检查后面的结点是否有非空结点。 p=Q[++front]; if(p!=NULL)return 0; } } } return 1; } //把二叉树所有结点的左右子树进行交换,如果用中序遍历,恰好反序。 void Exchange(BiTree T){ if(T!=NULL){ BiTree temp; Exchange(T->lchild); Exchange(T->rchild); temp=T->lchild; T->lchild=T->rchild; T->rchild=temp; } } int main(){ BiTree BT; int array[10]={10,5,6,55,99,2,1,3,4,7}; BST_Create(BT,array,10); printf("前序遍历(递归) ");PreOrder(BT);printf("\n"); printf("前序遍历2(非递归) ");PreOrder2(BT);printf("\n"); printf("中序遍历(递归) ");InOrder(BT);printf("\n"); printf("中序遍历2(非递归) ");InOrder2(BT);printf("\n"); printf("中序遍历3(非递归) ");InOrder3(BT);printf("\n"); printf("后序遍历1(递归) ");PostOrder(BT);printf("\n"); printf("后序遍历2(非递归) ");PostOrder2(BT);printf("\n"); printf("后序遍历3(非递归) ");PostOrder3(BT);printf("\n"); printf("层序遍历 ");LevelOrder(BT);printf("\n"); printf("层序遍历 (反过来) ");LevelOrderReverse(BT);printf("\n"); printf("树的高度(递归) ");printf("%d ",Height(BT));printf("\n"); printf("树的高度(非递归) ");printf("%d ",Height1(BT));printf("\n"); printf("双分支数(递归) ");printf("%d ",TwoBranchNum(BT));printf("\n"); // printf("双分支数(递归) ");TwoBranchNum1(BT);printf("%d ",twonum);printf("\n"); printf("双分支数(递归) ");printf("%d ",TwoBranchNum2(BT));printf("\n"); printf("双分支数(非递归) ");printf("%d ",TwoBranchNum3(BT));printf("\n"); printf("单分支数(递归) ");printf("%d ",OneBranchNum(BT));printf("\n"); printf("是否完全二叉树 ");printf("%d ",isCompleted(BT));printf("\n"); printf("交换左右子树 ");Exchange(BT); InOrder(BT);printf("\n"); return 1; }
用到的方法函数,如前序遍历,中序遍历,后序遍历,交换左右子树,求树的高度,是否完全二叉树,双分支数,单分支结点数等等。
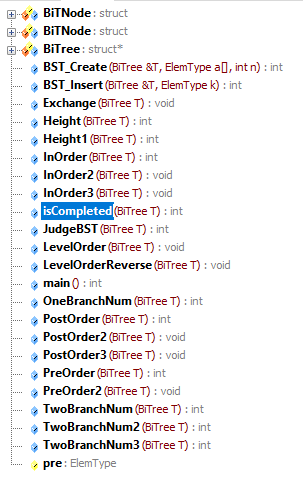
这是运行结果:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号