【排序】【规律】Codeforces Round #431 (Div. 2) - D. Rooter's Song

D. Rooter's Song

Source

http://codeforces.com/contest/849/problem/D

Description

Wherever the destination is, whoever we meet, let's render this song together.

On a Cartesian coordinate plane lies a rectangular stage of size w × h, represented by a rectangle with corners (0, 0), (w, 0), (w, h) and (0, h). It can be seen that no collisions will happen before one enters the stage.

On the sides of the stage stand n dancers. The i-th of them falls into one of the following groups:

• Vertical: stands at (x_i, 0), moves in positive y direction (upwards);
• Horizontal: stands at (0, y_i), moves in positive x direction (rightwards).

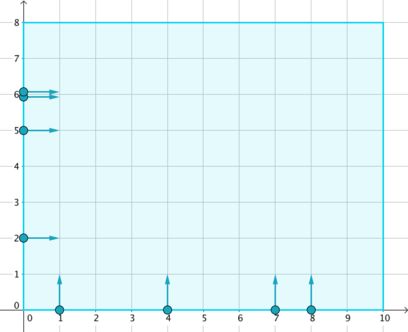
According to choreography, the i-th dancer should stand still for the first t_i milliseconds, and then start moving in the specified direction at 1 unit per millisecond, until another border is reached. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.

When two dancers collide (i.e. are on the same point at some time when both of them are moving), they immediately exchange their moving directions and go on.

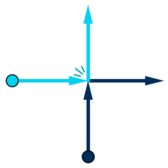
Dancers stop when a border of the stage is reached. Find out every dancer's stopping position.

Input

The first line of input contains three space-separated positive integers n, w and h (1 ≤ n ≤ 100 000, 2 ≤ w, h ≤ 100 000) — the number of dancers and the width and height of the stage, respectively.

The following n lines each describes a dancer: the i-th among them contains three space-separated integers g_i, p_i, and t_i (1 ≤ g_i ≤ 2, 1 ≤ p_i ≤ 99 999, 0 ≤ t_i ≤ 100 000), describing a dancer's group g_i (g_i = 1 — vertical, g_i = 2 — horizontal), position, and waiting time. If g_i = 1 then p_i = x_i; otherwise p_i = y_i. It's guaranteed that 1 ≤ x_i ≤ w - 1 and 1 ≤ y_i ≤ h - 1. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.

Output

Output n lines, the i-th of which contains two space-separated integers (x_i, y_i) — the stopping position of the i-th dancer in the input.

Examples

Input

8 10 8
1 1 10
1 4 13
1 7 1
1 8 2
2 2 0
2 5 14
2 6 0
2 6 1

Output

4 8
10 5
8 8
10 6
10 2
1 8
7 8
10 6

Input

3 2 3
1 1 2
2 1 1
1 1 5

Output

1 3
2 1
1 3

 

Note

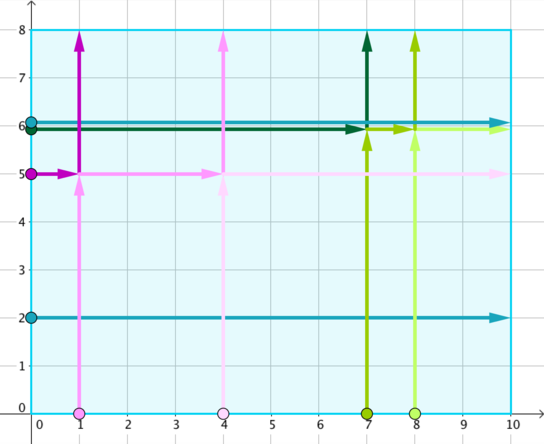
The first example corresponds to the initial setup in the legend, and the tracks of dancers are marked with different colours in the following figure.

In the second example, no dancers collide.

Solution

挺不错的一题，官方题解讲得也挺详细的：

How to deal with "waiting time"?

Move every dancer t_i units backwards in the first place, that is to (x_i - t_i, 0) for the vertical-moving group, and (0, y_i - t_i) for the horizontal-moving group. Then start the time, making everyone start moving immediately.

When do dancers collide? What changes and what keeps the same?

Notice that if two dancers collide before any other collision happens, then they have the same x + y values for their initial positions. Furthermore, after a collision, the two dancers keep having the same x + y, and also with the same relative orders of x and y. Also, after a collision, the union of all dancers' tracks will be the same as if they "went through" each other and no collision happened at all (see the figure for sample 1 to get a general idea on this).

Therefore, divide dancers into groups by p_i - t_i, and collisions will happen within groups only. Dancers in the same group will move on the same x + y line (a line of slope  - 1), and however collisions take place, they will keep current relative order of x and y. It's proved before that in each group, dancers' exiting positions is the same as if no collision happened at all (namely, (x_i, h) for initially-vertical dancers, and (w, y_i) for initially-horizontal ones). For each group, find out all such positions. Sort all dancers according to their initial x values, and sort these positions in the direction of (0, h) to (w, h) then (w, 0). Match the sorted dancers to these sorted positions and obtain the answers for all dancers. This solution works in .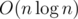

注意排序的顺序，附上自己的代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn = 100100;

struct Node{
    int x,y;
}Ans[maxn];

int n,w,h,g[maxn],p[maxn],t[maxn];
vector<vector<int>>grp(2*maxn);
vector<vector<Node>>res(2*maxn);

bool cmp1(int a,int b){
    if(g[a] != g[b]) return g[a] > g[b];
    if(g[a] == 2) return p[a] > p[b];
    return p[a] < p[b];
}

bool cmp2(Node a,Node b){
    if(a.y == h && b.x == w) return 1;
    if(a.x == w && b.y == h) return 0;
    if(a.y == h) return a.x < b.x;
    return a.y > b.y;
}

int main(){
    cin >> n >> w >> h;
    for(int i = 1;i <= n;++i){
        scanf("%d%d%d",&g[i],&p[i],&t[i]);
        if(g[i] == 1){
            grp[p[i]-t[i]+100000].push_back(i);
            res[p[i]-t[i]+100000].push_back({p[i],h});
        }
        else{
            grp[p[i]-t[i]+100000].push_back(i);
            res[p[i]-t[i]+100000].push_back({w,p[i]});
        }
    }
    for(int i = 0;i < 200000;++i){
        if(grp[i].empty()) continue;
        sort(grp[i].begin(),grp[i].end(),cmp1);
        sort(res[i].begin(),res[i].end(),cmp2);
        for(int j = 0;j < grp[i].size();++j) Ans[grp[i][j]] = res[i][j];
    }
    for(int i = 1;i <= n;++i) printf("%d %d\n",Ans[i].x,Ans[i].y);

    return 0;
}