【乱搞】【随机】Codeforces Round #254 (Div. 2) - D. DZY Loves FFT

D. DZY Loves FFT

Source

http://codeforces.com/contest/445/problem/D

Description

DZY loves Fast Fourier Transformation, and he enjoys using it.

Fast Fourier Transformation is an algorithm used to calculate convolution. Specifically, if a, b and c are sequences with length n, which are indexed from 0 to n - 1, and

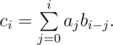
We can calculate c fast using Fast Fourier Transformation.

DZY made a little change on this formula. Now

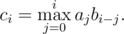
To make things easier, a is a permutation of integers from 1 to n, and b is a sequence only containing 0 and 1. Given a and b, DZY needs your help to calculate c.

Because he is naughty, DZY provides a special way to get a and b. What you need is only three integers n, d, x. After getting them, use the code below to generate a and b.

//x is 64-bit variable;
function getNextX() {
    x = (x * 37 + 10007) % 1000000007;
    return x;
}
function initAB() {
    for(i = 0; i < n; i = i + 1){
        a[i] = i + 1;
    }
    for(i = 0; i < n; i = i + 1){
        swap(a[i], a[getNextX() % (i + 1)]);
    }
    for(i = 0; i < n; i = i + 1){
        if (i < d)
            b[i] = 1;
        else
            b[i] = 0;
    }
    for(i = 0; i < n; i = i + 1){
        swap(b[i], b[getNextX() % (i + 1)]);
    }
}

Operation x % y denotes remainder after division x by y. Function swap(x, y) swaps two values x and y.

 

Input

The only line of input contains three space-separated integers n, d, x (1 ≤ d ≤ n ≤ 100000; 0 ≤ x ≤ 1000000006). Because DZY is naughty, x can't be equal to 27777500.

Output

Output n lines, the i-th line should contain an integer c_i - 1.

Examples

Input

3 1 1

Output

1
3
2

Input

5 4 2

Output

2
2
4
5
5

Input

5 4 3

Output

5
5
5
5
4

Note

In the first sample, a is [1 3 2], b is [1 0 0], so c₀ = max(1·1) = 1, c₁ = max(1·0, 3·1) = 3, c₂ = max(1·0, 3·0, 2·1) = 2.

In the second sample, a is [2 1 4 5 3], b is [1 1 1 0 1].

In the third sample, a is [5 2 1 4 3], b is [1 1 1 1 0].

 

Solution

从a[]和b[]的生成方式可以看出这两个序列是几乎随机的。

优先队列维护从a[0]到a[i]的前50大的数，每次从里面从大到小地找有没有元素对应的b是等于1的，若有那么就是答案，若没有的话那就暴力跑一次a[0]...a[i]。注意有时候序列b里会有很多0，导致很多位置都无法在第一步就找到答案，所以预处理出所有使得b[i] != 0的i，这样会大大减小暴力跑时的耗时。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
ll n,d,x,a[100111],b[100111];
priority_queue<pair<ll,int>> que;

ll getNextX() {
    x = (x * 37 + 10007) % 1000000007;
    return x;
}
void initAB() {
    int i;
    for(i = 0; i < n; i = i + 1){
        a[i] = i + 1;
    }
    for(i = 0; i < n; i = i + 1){
        swap(a[i], a[getNextX() % (i + 1)]);
    }
    for(i = 0; i < n; i = i + 1){
        if (i < d)
            b[i] = 1;
        else
            b[i] = 0;
    }
    for(i = 0; i < n; i = i + 1){
        swap(b[i], b[getNextX() % (i + 1)]);
    }
}

int main(){
    cin >> n >> d >> x;
    initAB();
    vector<int> vb;
    for(int i = 0;i < n;++i) if(b[i]) vb.push_back(i);
    for(int i = 0;i < n;++i){
        que.push({a[i],i});
        bool found = 0;
        priority_queue<pair<ll,int>> tmp;
        for(int j = 0;!que.empty() && j < 50;++j){
            ll t = que.top().first;
            int id = que.top().second;
            if(!found && b[i-id]){
                printf("%lld\n",t);
                found = 1;
            }
            tmp.push(que.top());
            que.pop();
        }
        if(!found){
            ll ans = 0;
            for(int j = 0;j < vb.size() && vb[j] <= i;++j)
                ans = max(ans,a[i-vb[j]]);
            printf("%lld\n",ans);
        }
        que = tmp;
    }

    return 0;
}