【构造】【规律】Codeforces Round #431 (Div. 2) - C. From Y to Y

C. From Y to Y

Source

http://codeforces.com/contest/849/problem/C

Description

From beginning till end, this message has been waiting to be conveyed.

For a given unordered multiset of n lowercase English letters ("multi" means that a letter may appear more than once), we treat all letters as strings of length 1, and repeat the following operation n - 1 times:

• Remove any two elements s and t from the set, and add their concatenation s + t to the set.

The cost of such operation is defined to be 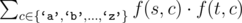, where f(s, c) denotes the number of times character c appears in string s.

Given a non-negative integer k, construct any valid non-empty set of no more than 100 000 letters, such that the minimum accumulative cost of the whole process is exactly k. It can be shown that a solution always exists.

Input

The first and only line of input contains a non-negative integer k (0 ≤ k ≤ 100 000) — the required minimum cost.

Output

Output a non-empty string of no more than 100 000 lowercase English letters — any multiset satisfying the requirements, concatenated to be a string.

Note that the printed string doesn't need to be the final concatenated string. It only needs to represent an unordered multiset of letters.

Examples

Input

12

Output

abababab

Input

3

Output

codeforces

 

 

Note

For the multiset {'a', 'b', 'a', 'b', 'a', 'b', 'a', 'b'}, one of the ways to complete the process is as follows:

• {"ab", "a", "b", "a", "b", "a", "b"}, with a cost of 0;
• {"aba", "b", "a", "b", "a", "b"}, with a cost of 1;
• {"abab", "a", "b", "a", "b"}, with a cost of 1;
• {"abab", "ab", "a", "b"}, with a cost of 0;
• {"abab", "aba", "b"}, with a cost of 1;
• {"abab", "abab"}, with a cost of 1;
• {"abababab"}, with a cost of 8.

The total cost is 12, and it can be proved to be the minimum cost of the process.

Solution

题意：很简单自己读。

稍加观察可以发现：给你n个a和n个b，那么以ababab...这样的顺序，一次只合并一个字母进去，最后得到的结果是最小的，并且这个结果很容易算出来。那么就可以递归解决了，如k=14时，先得到abababab，这里已经有了12，再得到cdcd，这里是2，加起来就是14了。写起来其实很简单，具体看代码，我写得略蠢。

也可以aaaaaabbb...这种构造，因为aaaaa...(n个）贡献的答案是n*(n-1)/2，同样可以用递归解决，当时没想到。。

#include<bits/stdc++.h>
using namespace std;

int n;

void solve(int k,char s){
    int now = 0,cnt = 0;
    while(cnt + now <= k){
        putchar(s);
        cnt += now;
        if(cnt + now > k) break;
        putchar(s+1);
        cnt += now;
        now++;
    }
    if(k-cnt) solve(k-cnt,s+2);
}

int main(){
    cin >> n;
    solve(n,'a');

    return 0;
}