多边形入门 ——toj1813 A Round Peg in a Ground Hole
题目大意:
平面上有一个多边形的孔,给定一个圆形钉子的圆心坐标和半径,问能否放进去。如果孔是多边形则输出“HOLE IS ILL-FORMED“,否则输出能否放进去。
首先,我们需要判断一个多边形是不是凸多边形。我们只需要枚举各个边,看其他所有顶点是不是在它的同测。但是需要注意一个问题,有可能数据中有三点共线,开始我就是坐在这里挂了。代码如下:
{
int t,tt,pre;
for(t=0;t<n;t++)
{
tt=0;
while(pre=sign(crossP(vpt[t],vpt[(t+1)%n],vpt[(t+2+tt)%n])),pre==0)
tt++;
for(;tt<n-2;tt++)
{
double d=crossP(vpt[t],vpt[(t+1)%n],vpt[(t+2+tt)%n]);
if(sign(d)==0)
continue;
if(sign(d)!=pre)
return false;
}
}
return true;
}
接下来,我们就需要考虑一个多边形里头能不能放下一个指定的圆了。简单分析一下:
问题的实质是一个点到各个边的距离大于等于半径,而且点在多边形内。
先看距离问题,我首先想到的是集训时讲到的判断点到线段的距离,只要点到所有边的距离都大于半径就可以了。那么这样写首先要判断点在线段所在直线的投影跟线段的关系,如果在线段上,则返回垂足到点的距离,否则返回两端点到点的距离的最小值。这需要判断点的投影跟线段的关系,需要求垂足,比较复杂。
在fifth的提示下,得到如下思路:
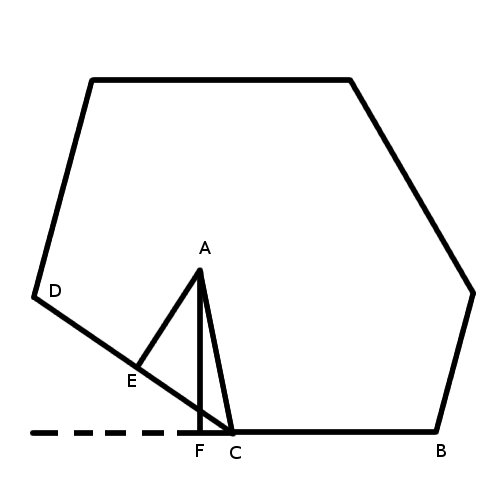
我们可以知道,只要圆的半径小于等于圆心到各边距离的最小值即可放入钉子。如果A点的投影在线段CB之外,比如F。那么|AF|>|AC|。但是很显然,|AE|>|AF|。那么我们需要用来比较的那个最小值并不会因此改变。所以,我们只需要在点到各边所在直线的距离中找出最小值,这个最小值必然等于我们最开始需要找的那个最小值。至此,问题大大化简。
接着,我么考虑边判断点是否早多边形内。
由于题目的特殊性,我们在此题中只需判断一个点是否在凸多边形内。如果注意到这点,就不必考虑复杂的凹多边形。那么,只要判断该点是否在所有边的同侧即可。代码如下:
{
int t;
PT st,end;
int dr=sign(crossP(vpt[0],vpt[1],pt));
for(t=1;t<n;t++)
{
st=vpt[t];
end=vpt[(t+1)%n];
if(sign(crossP(st,end,pt))!=dr)
return false;
}
return true;
}
那么最后,判断是否适合的函数可以这么写:
{
if(!inPoly(vpt,pt))
return false;
int t,tt;
PT st,end;
for(t=0;t<n;t++)
{
st=vpt[t];
end=vpt[(t+1)%n];
double d=fabs(crossP(st,end,pt))/dis(st,end);
if(sign(R-d)==1)
return false;
}
return true;
总结一下:
最大的收获是,对于一个几何题目,要充分发掘其几何性质,不要看到一个问题就想套用模板。多思考一下往往能够比模板带来更大的方便。另外,几何题目一定要考虑完全特殊情况,边界情况,才能做到万无一失。



