加权区间调度问题
问题描述:给定n个job,每个活动i的开始时间和结束时间,对应一个权值,找出权值之和最大的相容活动子集。(若两个job的时间不相交,则称两个活动是相容的compatible)
方案一(递归算法)
算法设计:
OPT(j): //j个活动求相容活动子集的最大权值
If j == 0 then
return 0
Else
return max(OPT(p(j)) + vj, OPT(j-1))
Endif
算法分析:
算法时间复杂度:自顶而下的递归算法是指数时间的,因为会重复计算子问题,不带记忆性,时间复杂度大概是O(1.618^n)(介于根号2^n~2^n)。
算法空间复杂度:O(n),需要大小为n的数组存储每个子问题的解。
程序设计:
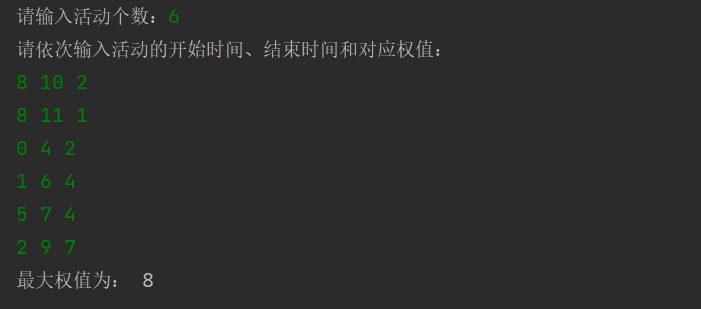
1 n = int(input('请输入活动个数:')) 2 list_act = [[0 for i in range(3)] for j in range(n)] 3 for i in range(0, n): 4 list_act[i][0] = int(input('请输入第{}活动开始时间:'.format(i+1))) 5 list_act[i][1] = int(input('请输入第{}活动结束时间:'.format(i+1))) 6 list_act[i][2] = int(input('请输入第{}活动权值:'.format(i+1))) 7 print(list_act) 8 9 pre = [0] * n 10 for i in range(1, n): 11 for j in range(i-1, -1, -1): 12 if list_act[j][1] <= list_act[i][0]: 13 pre[i] = j + 1 14 break 15 print(pre) 16 17 def option(n): 18 if n == 0: 19 return 0 20 if n >= 1: 21 if option(pre[n-1]) + list_act[n-1][2] >= option(n-1): 22 return option(pre[n-1]) + list_act[n-1][2] 23 else: 24 return option(n-1) 25 26 print('相容活动权值之和最大是:', option(n)) 27 28 record = [[0 for i in range(2)] for j in range(n)] 29 for i in range(1 , n+1): 30 if option(pre[i-1]) + list_act[i-1][2] >= option(i-1): 31 record[i-1][0] = 1 32 record[i-1][1] = pre[i-1] 33 else: 34 record[i-1][0] = 0 35 record[i-1][1] = i - 1 36 37 for i in range(1 , n+1): 38 j = record[i-1][1] 39 if j > 0 and record[j-1][0] == 1: 40 print('第{}个活动将被选择'.format(j))
结果输出:

方案二(动态规划算法)
算法设计:
1.输入活动的开始时间、结束时间和对应权值,存储在列表 job 中,并按照结束时间的早晚对活动进行排序,存储在列表 jobp 中。
2.使用动态规划的思想,定义两个数组 p 和 m,其中 p[i] 表示在选择前 i 个活动中,最后一个活动的索引,即 jobp[p[i]] 是最后一个被选择的活动;m[i] 表示选择前 i 个活动的最大权值和。
3.初始化 p 和 m 数组,p[0] = m[0] = 0。
4.对于每个活动 i,从前往后遍历,找到第一个不与前一个活动冲突的活动 j,即满足 jobp[i]['s'] >= jobp[j]['e']。然后将 j 的索引赋值给 p[i]。
5.使用备忘录数组 memo 来记录每个子问题的解,避免重复计算。对于每个活动 i,计算选择前 i 个活动的最大权值和,即 memo[i] = max(jobp[i]['v'] + memo[p[i]], memo[i - 1])。然后将 memo[i] 的值存储在数组 m 中。
6.返回 m[n],即选择所有活动的最大权值和。
算法分析:
算法的时间复杂度为 O(n^2),其中 n 是活动的个数。
算法的空间复杂度为 O(n),需要使用一个大小为 n 的备忘录数组来存储每个子问题的解。
程序设计:
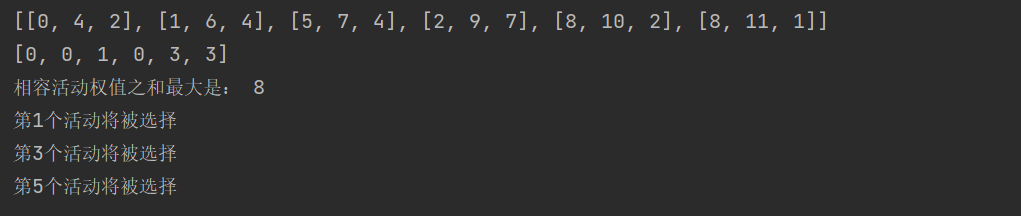
1 def solve(n): 2 p = [0] * (n + 1) 3 m = [0] * (n + 1) 4 memo = [0] * (n + 1) 5 job = [{'s': 0, 'e': 0, 'v': 0, 'index': 0} for _ in range(n + 1)] 6 print("请依次输入活动的开始时间、结束时间和对应权值:") 7 for i in range(1, n + 1): 8 s, e, v = map(int, input().split()) 9 job[i]['s'], job[i]['e'], job[i]['v'] = s, e, v 10 job[i]['index'] = i 11 jobp = sorted(job, key=lambda x: x['e'],reverse=False) 12 for index, dictionary in enumerate(jobp,start=0): 13 dictionary['index'] = index 14 for i in range(n, 0, -1): 15 for j in range(n-1, 0, -1): 16 if jobp[i]['s'] >= jobp[j]['e']: 17 p[i] = jobp[j]['index'] 18 break 19 for i in range(1, n + 1): 20 memo[i] = max(jobp[i]['v'] + memo[p[i]], memo[i - 1]) 21 m[i] = memo[i] 22 return m[n] 23 24 if __name__ == "__main__": 25 n = int(input("请输入活动个数:")) 26 result = solve(n) 27 print("最大权值为:",result)
结果输出: