比赛日程问题

问题描述：

1.设有n（n为任意值）个选手进行循环赛，手工设计一个满足以下要求的比赛日程表：

(1) 每个选手必须与其他n-1个选手各赛一次；

(2) 每个选手一天只能赛一次；

(3) 循环赛一共进行n-1天。

算法设计：

假设有N名选手参赛，不妨构造一个N×N的矩阵。在矩阵第一行填充1，2,…,N，第一列填充1，2,…,N。矩阵定义：把矩阵的第一列作为参赛选手的编号，第2~N列作为某一参赛选手的对手，显然任意的人数的选手其第一行都是一行选手，对手为2，3,…,N号选手，第一列是所有选手编号1，2，…,N。但是以上构造存在一个问题，就是这种假设默认了参赛选手人数是偶数，因为只有人数是偶数的情况下才只会需要N-1天（N-1列参赛选手）就完成比赛。所以我们不妨先考虑是选手是偶数的情况。

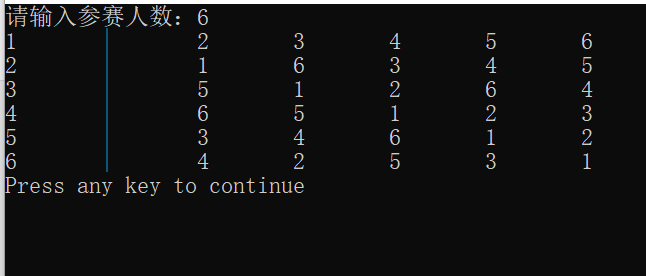
按照以上方法构造出来的答案如下（以N=6为例，取其它偶数情况亦同）：

从以上结果寻找规律：

  1. 对角线上的元素全部为1。
  2. 考虑所有与对角线平行的斜线，对于上半矩阵，将对角线作为第一条斜线，之后的第2,3,…,N-1条斜线上的取值全部依次为2,3,…,N-1。如果斜线中的某一行原本的要取的值与所在行数相同，则取最大值N（如图1，第二行第三列位于第二条斜线，原本要取2，当因为他也在第二行，故取最大值6）。对于下半矩阵，规律也是类似的，将对角线作为第一条斜线，之后的第2,3,…,N-1条斜线取值依次为N-1,N-2,N-3……。同样的如果要取的值与行数相同则取最大值N。

根据以上规律，我们得到当N等于偶数时算法设计的思路：

  1. 按照上述规律对上半矩阵赋值。
  2. 对下半矩阵赋值。
  3. 对于得到矩阵，由于其每一列的和必定为sum=1+2+⋯+N，故用sum减去前N-1列的值，得到该列最后一行的值。

然后考虑N为奇数的情况（以N=7为例,其它奇数情况亦同），构造矩阵情况如下：

由构造的结果发现，对于奇数情况，我们可以先为他添加1使其变为偶数人的情况，不同的是，当斜线上存在相同值时我们不是添加最大值，而是添加0（0表示轮空）。得到的结果矩阵删去最后一行就是我们所需要的结果了。所以对于偶数情况，我们的代码要改的地方就是将传入的N+1，然后相同值由添加N改为添加0即可。此外，由于删去了最后一行，我们不需要再考虑偶数时最后一行得到的值不正确的情况了，故不需要再对每一列求和。

算法分析：

时间复杂度：O(N^2)，因为有两个嵌套的for循环，每个循环的次数都是N。
空间复杂度：O(N^2)，因为创建了一个N*N的二维数组。

程序设计：

  1 #include <iostream>
  2 
  3 using namespace std;
  4 
  5 int a[101][101] = {0};
  6 
  7 int main(int argc, const char * argv[]) {
  8 
  9 int N, i, j, k;
 10 
 11 cout << "请输入参赛人数：";
 12 
 13 cin >> N; // 比赛人数
 14 
 15 for (i = 1; i <= N; i ++){
 16 
 17 a[1][i] = a[i][1] = i;
 18 
 19 a[i][i] = 1;
 20 
 21 }
 22 
 23 bool flag = true; // N为偶数
 24 
 25 // 偶数人
 26 
 27 if(N % 2 == 0){
 28 
 29 // 上半区对角线方向赋值
 30 
 31 for (i = 2; i <= N; i ++){
 32 
 33 for (j = 1; j <= N-i; j ++){
 34 
 35 if (j + 1 == i) {// 如果要赋的值与所在行数相同
 36 
 37 a[i][i+j] = N;// 赋予最大值
 38 
 39 continue;
 40 
 41 }
 42 
 43 a[i][i+j] = j + 1;
 44 
 45 }
 46 
 47 }
 48 
 49 // 下半区对角线方向赋值
 50 
 51 for (i = 3; i <= N; i ++){
 52 
 53 for (j = i - 1, k = N - 1; j > 1; j --){
 54 
 55 if (k == i){
 56 
 57 a[i][j] = N;
 58 
 59 k --;
 60 
 61 continue;
 62 
 63 }
 64 
 65 a[i][j] = k --;
 66 
 67 }
 68 
 69 }
 70 
 71 int sum = 0, ss = 0;
 72 
 73 for(i = 1; i <= N; i ++){
 74 
 75 sum += i;
 76 
 77 }
 78 
 79 for (i = 2; i <= N; i ++) {
 80 
 81 for (j = 1; j <= N - 1; j ++){
 82 
 83 ss += a[j][i];
 84 
 85 }
 86 
 87 a[j][i] = sum - ss;
 88 
 89 ss = 0;
 90 
 91 }
 92 
 93 }
 94 
 95 // 奇数人
 96 
 97 else{
 98 
 99 flag = false;
100 
101 N += 1;
102 
103 for (i = 2; i <= N; i ++){
104 
105 for (j = 1; j <= N; j ++){
106 
107 if (j + 1 == i) {// 如果要赋的值与所在行数相同
108 
109 a[i][i+j] = 0;// 赋予0
110 
111 continue;
112 
113 }
114 
115 a[i][i+j] = j + 1;
116 
117 }
118 
119 }
120 
121 // 下半区对角线方向赋值
122 
123 for (i = 3; i <= N; i ++){
124 
125 for (j = i - 1, k = N - 1; j > 1; j --){
126 
127 if (k == i){
128 
129 a[i][j] = 0;
130 
131 k --;
132 
133 continue;
134 
135 }
136 
137 a[i][j] = k --;
138 
139 }
140 
141 }
142 
143 }
144 
145 
146 
147 if(flag){
148 
149 for (i = 1; i <= N; i ++) {
150 
151 for (j = 1; j <= N; j ++){
152 
153 cout << a[i][j] << "\t";
154 
155 if (j == 1){
156 
157 cout << "|\t";
158 
159 }
160 
161 }
162 
163 cout << endl;
164 
165 }
166 
167 }
168 
169 else{
170 
171 for (i = 1; i <= N - 1; i ++) {
172 
173 for (j = 1; j <= N; j ++){
174 
175 cout << a[i][j] << "\t";
176 
177 if (j == 1){
178 
179 cout << "|\t";
180 
181 }
182 
183 }
184 
185 cout << endl;
186 
187 }
188 
189 }
190 
191 return 0;
192 
193 }

结果输出：

posted @ 2024-01-20 17:25  棒打鲜橙不加冰  阅读(13)  评论(0)  编辑  收藏  举报