RSA加密算法实现

一、实验目的

深度理解RSA算法的工作原理，查阅欧几里得扩展算法计算模运算的逆元，并编程序实现。学会生成不同大小的素数，体会模指数运算的困难性和模指数运算的快速算法。

二、实验器材

pycharm+python3.11

三、实验内容

1.实验要求：自己配置python环境，编写RSA算法实现程序，运行RSA程序，演示RSA加密与解密的过程。

RSA加密过程：

（1）编写程序调用gmpy.2的大素数生成算法，生成不同的素数。

程序代码：

import gmpy2
from gmpy2 import mpz
def gen_prime(rs):
    """生成二进制位数为1024的随机素数"""
    p = gmpy2.mpz_urandomb(rs, 1024)
    while not gmpy2.is_prime(p):
        p = p + 1
    return p

（2）编写RSA程序，在程序中调用大素数生成算法生成需要的素数。

程序代码：

import gmpy2
from gmpy2 import mpz
import binascii


def gen_prime(rs):
    """生成二进制位数为1024的随机素数"""
    p = gmpy2.mpz_urandomb(rs, 1024)
    while not gmpy2.is_prime(p):
        p = p + 1
    return p


def gen_key():
    """生成密钥"""
    rs = gmpy2.random_state()
    p = gen_prime(rs)
    q = gen_prime(rs)
    return p, q


def encrypt(e, n, message):
    """将输入消息转换成16进制数字并加密，支持utf-8字符串"""
    M = mpz(binascii.hexlify(message.encode('utf-8')), 16)
    C = gmpy2.powmod(M, e, n)
    return C


def decrypt(d, n, C):
    """对输入的密文进行解密并解码"""
    M = gmpy2.powmod(C, d, n)
    return binascii.unhexlify(format(M, 'x')).decode('utf-8')


def main():
    # 密钥生成
    p, q = gen_key()
    n = p * q
    phi = (p - 1) * (q - 1)
    e = 3674911
    d = gmpy2.invert(e, phi)

    # 输入消息
    message = input('输入待加密的消息：\n')

    # 加密
    C = encrypt(e, n, message)
    print('16进制密文：', hex(C))

    # 解密
    print('解密后的消息：', decrypt(d, n, C))


if __name__ == '__main__':
    main()

运行结果：

（3）用较小的x<1,000,000,000尝试采用传统方法计算模指数，即a^x+1 mod n = [ (a^x mod n) ×  a] mod n 的方法。

程序代码：

from math import sqrt

def Cnotrol():
d = 0
x = int(input('请输入你的选择的功能::RSA加密为0，RSA解密为1，分解查找P与Q为2,退出请按9:'))
qt = 1
while qt:
if x == 0:
print('----------------加密----------------')
print('---------请输入P,Q,E,M(明文)---------')
p = int(input('输入P:'))
q = int(input('输入Q:'))
e = int(input('输入E:'))
Flag = apnjudg(p, q, e)
if Flag == 0:
m = int(input('请输入M:'))
encryption(m, e, p * q)
Cnotrol()
else:
break
elif x == 1:
print('----------------解密----------------')
print('---------请输入P,Q,E,C(密文)---------')
p = int(input('输入P:'))
q = int(input('输入Q:'))
e = int(input('输入E:'))
fi = (p - 1) * (q - 1)
for i in range(fi): # 求逆元d
if e * i % fi == 1:
d = i
break
print("逆元d的值为：", d)
apnjudg(p, q, d)
c = int(input('请输入C:'))
decode(c, d, p * q)
Cnotrol()

elif x == 2:
print('----------------拆解素数乘积----------------')
n = int(input('输入乘积N:'))
broken(n)
Cnotrol()

else:
print("感谢您的使用")
break
qt = 0
def encryption(m, e, n)://传统方法计算模指数
s = m % n
for i in range(1, e):
s = (s * (m % n)) % n
print('你所加密的密文是：', s)
# 解密
def decode(c, d, n):
s = c % n
for i in range(1, d):
s = (s * (c % n)) % n
print('你所解密的明文是：', s)
# p,q,e质数判断
def apnjudg(p, q, e):
Li = [p, q, e]
flag = 0
for x in range(0, 3):
if int(Li[x]) > 2:
# 查看因子
# sqrt()平方根函数减小计算周期
for i in range(2, int(sqrt(Li[x]))+1):
if (int(Li[x]) % i) == 0:
print(int(Li[x]), "不是质数")
print(i, "乘于", int(Li[x]) // i, "是", int(Li[x]))
flag += 1
break
else:
continue
if flag == 0:
print(int(Li[x]), "是质数")
else:
print("QAQ您的输入有误(存在非质数)，程序退出QAQ")
break
# 如果输入的数字小于或等于 2，不是质数
else:
print(int(Li[x]), "不是质数")
flag += 1
continue
return flag
# 拆解获得素数p,q
def broken(n):
if n < 10000000:
for i in range(1, 10000):
for t in range(1, 10000):
if n == i * t:
print(i, t)
break
if __name__ == '__main__':
Cnotrol()

运行结果：

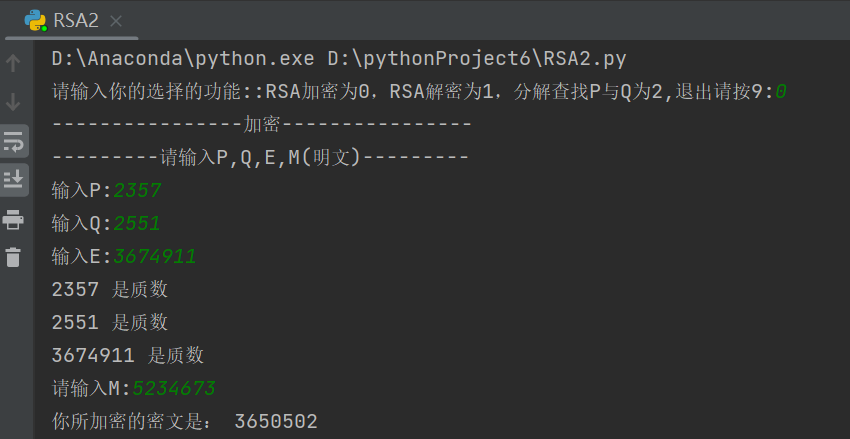
(4)尝试用模运算的快速算法计算模指数(称为重复平方相乘法)，即将指数写成二进制的形式，如果b=35，可以写成b=1000011，则

a^b mod n = (a³²)¹*(a¹⁶)⁰*(a⁸)⁰*(a⁴)⁰*(a²)⁰*(a¹)¹*(a⁰)¹ mod n

算法原理：

程序代码：

def fastExpMod(b,n,m):
'''
return : b^n mod m
'''
result = 1
while n != 0:
if (n & 1) == 1: #按位与&操作
result = (result * b) % m
b = (b*b) % m
n = n >> 1 #位数右移>>操作
return result

(5)利用快速模指数运算法实现RSA加密与解密算法

程序代码：

'''
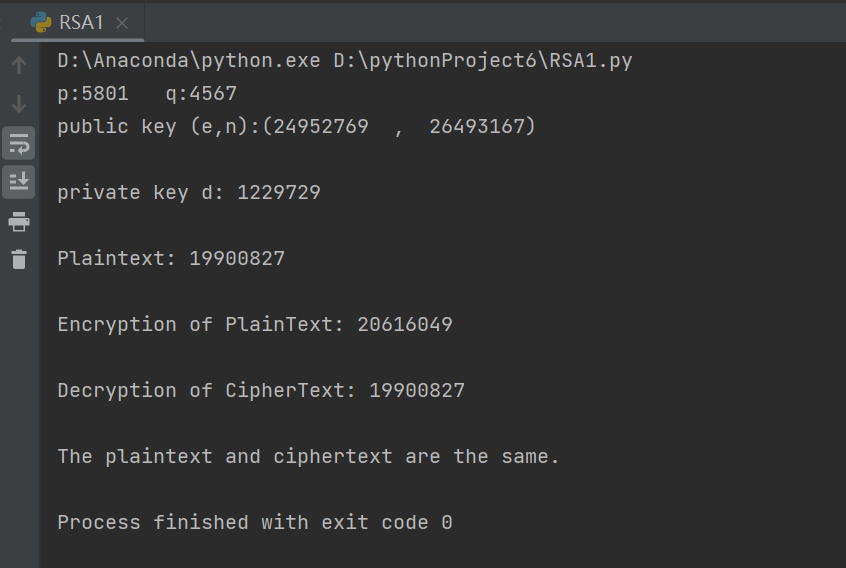
RSA加解密算法
2023.11.11
1.模平方算法 2.欧几里得算法 3.费马素性检测算法
'''
import random


def fastExpMod(b, n, m):
'''
return : b^n mod m
'''
result = 1
while n != 0:
if (n & 1) == 1: # 按位与操作
result = (result * b) % m
b = (b * b) % m
n = n >> 1 # 位数右移操作
return result


def Euclid(a,b):
'''
欧几里得算法 ax + by = gcd(a,b)
Return : [x , y , gcd(a,b)]
'''
X = [1,0,a]
Y = [0,1,b]
while Y[2] !=0 :
Q = X[2]//Y[2]
NEW_Y = [i*Q for i in Y]
T = list(map(lambda x: x[0]-x[1], zip(X, NEW_Y)))
X = Y.copy()
Y = T.copy()
return X


def fermatPrimeTest(m, k):
'''
费马素性检验算法
m : 给定整数
k : 安全参数，重复K次
'''
if m % 2 == 0:
return False
for i in range(k):
a = random.randint(2, m - 2)
g = Euclid(a, m)
if g[2] == 1:
r = fastExpMod(a, m - 1, m)
if r == 1:
continue
else:
return False
else:
return False
return True
def findPrime(lower, upper):
'''
return : 一个位于upper和lower之间的素数
'''
while True:
n = random.randint(lower, upper)
if fermatPrimeTest(n, 6) == True:
return n


def selectE(fn):
'''
fn : euler function
Return : e
'''
while True:
e = random.randint(1, fn)
temp = Euclid(e, fn)
if temp[2] == 1:
return e


def keyGenerate(lower, upper):
'''
给定两个素数p和q生成的区间
return : e,n,d
'''
p = findPrime(lower, upper)
q = findPrime(lower, upper)
print("p:" + str(p) + " q:" + str(q))
# print("q:"+str(q))
n = p * q
fn = (p - 1) * (q - 1)
e = selectE(fn)
temp = Euclid(e, fn) # 欧几里得算法求逆元
d = temp[0]
if d < 0: # 由于e和fn互素故一定存在逆元
d = d + fn # 保证d为正数
return e, n, d


def start():
e, n, d = keyGenerate(1000, 10000) # 密钥生成
# 更改keyGenerate函数的两个参数，可以改变生成素数的位数大小。
print("public key (e,n):", end="")
print("(" + str(e) + " , " + str(n) + ")\n")
print("private key d: " + str(d) + "\n")
m = random.randint(1, n) # m < n m为明文
print("Plaintext: " + str(m))
c = fastExpMod(m, e, n) # 加密 c为密文 m^e mod n
print("\nEncryption of PlainText: " + str(c))
x = fastExpMod(c, d, n) # 解密 c^d mod n
print("\nDecryption of CipherText: " + str(x))
if x == m:
print("\nThe plaintext and ciphertext are the same.")


if __name__ == "__main__":
start()

运行结果：