动态规划——最长公共子序列问题

动态规划 ——[蓝桥杯 2016 省 A] 密码脱落

在补题解的时候找到一篇回文字符串的题目，思考过后发现是一道动态规划中的最长公共子序列的题目。记录一下，以后遇见这类题，就可以做了
题解：首先拿到字符串，因为是找不同的数，我们可以反转字符串，找公共子序列，然后用总长度减去公共子序列的长度即可。
这里需要明白一个概念就是最长公共子序列的算法，如果找到相同的值就拿它左上角的数的值加1，否则找它上面的数或者左边的数之中取最大值赋值给当前的数

题目如下：

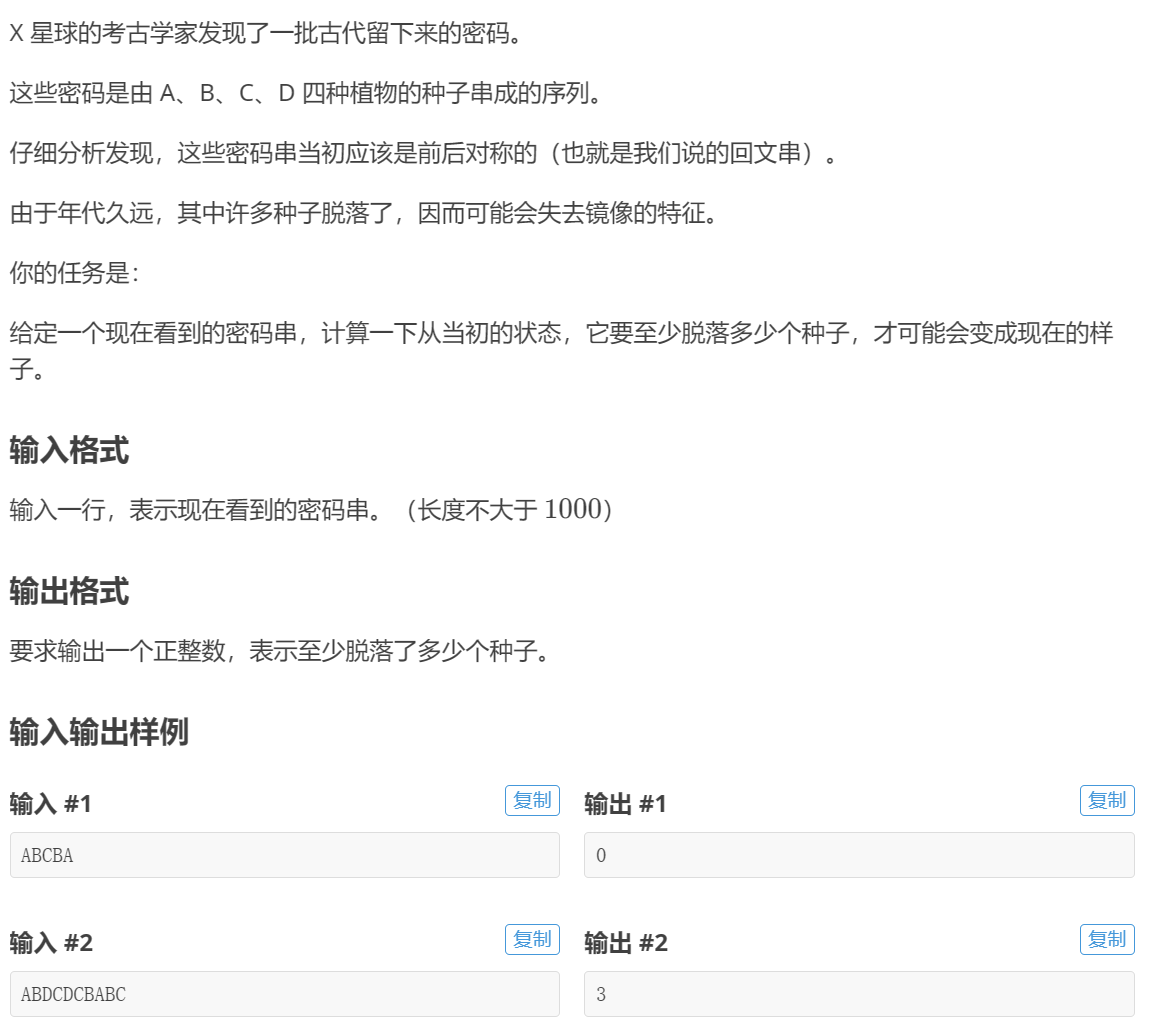
代码如下：

点击查看代码

#include <bits/stdc++.h>
using namespace std;
int f[1005][1005];//二维存储
int main ()
{
	//求最长公共子序列的长度，动态规划
	int ans = 0;
	string s;
	cin>>s;
	string s2 =s;
	int l =s.length();
    reverse(s.begin(),s.end());
	for(int i=1;i<=l;++i)			
		for(int j=1;j<=l;++j)
			if(s[i-1]==s2[j-1])	f[i][j]=f[i-1][j-1]+1;
               //如果找到一样的值就从它的左上角的值加一> > 
	else	f[i][j]=max(f[i][j-1],f[i-1][j]);
               //如果没有找到的话，就从它的左边或者是上边的值中的最大一个存储进当前的点
	cout<<l-f[l][l];
	return 0;
	cout<<ans;
}
//还有一个求最长公共字串，也是动态规划，可以进一步了解

最长公共子序列的模板代码

点击查看代码

for(int i=1;i<=lens;i++)//模板
		for(int j=1;j<=lens;j++)
			if(s1[i]!=s2[j]) f[i][j]=max(f[i-1][j],f[i][j-1]);
			else f[i][j]=f[i-1][j-1]+1;
	cout << lens-f[lens][lens];//输出