P3275 [SCOI2011]糖果 题解
一道差分约束的模板题。
题意：n个人每个人至少一个糖果，另外要满足k个不等式，求最少糖果数。
差分约束系统
给定一组不等式 $ x[i]-x[j]<=c[k] $ (或 $ x[i]-x[j]>=c[k] $ )，需要求出满足所有不等式的一组解 $ (x[1],x[2],…,x[n]) $ 。这类问题是线性规划的一类简单问题。
形式：通常表示为 $ AX<=C(或AX>=C) $ ，其中系数矩阵 $ A $ 的每一行里有一个 $ 1 $ 和一个 $ -1 $ ，其余元素都为 $ 0 $。若 $ A $ 为 $ m* n $的矩阵，则 $ X $ 为 $ n* 1 $ 的矩阵，$ C $ 为 $ m* 1 $ 的矩阵，对应有 $ m $ 个不等式，$ n $ 个未知数，即该系统为一个有 $ n $ 个未知数、$ m $ 个约束条件的系统，这就是差分约束系统。
求解差分约束系统，可以转化成图论的单源最短路径问题
$ x[j]-x[i]<=b[k] $ ，类似最短路中的三角不等式 $ d[j] <= d[i] + w[i,j] $ ，即 $ d[j] - d[i] <= w[i,j] $
以每个变量 $ x[i] $ 为结点，对于约束条件 $ x[j]-x[i]<=b[k] $ ，连接一条边 $ E(i,j) $ ，边权为 $ b[k] $
增加一个源点S与所有其他点相连，边权均为 $ 0 $ ， $ x[i]-x[0]<=0 $
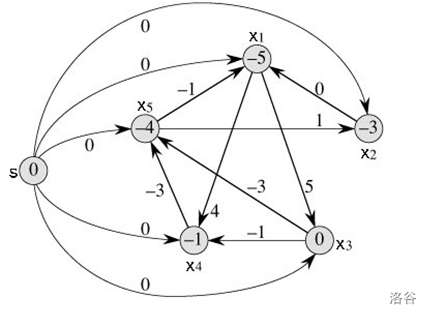
则引例中的不等式可以转化为如下有向图:
x1-x2<=0
x1-x5<=-1
x2-x5<=1
x3-x1<=5
x4-x1<=-1
x4-x3<=-1
x5-x3<=-3
x5-x4<=-3
最短路和最长路的区分
若求最大的解，那么初始时把 $ d[] $ 设为无穷大，用最短路求解。即 $ if(d[v]>d[u]+w(u,v)) $ 进行更新，而建图的时候也要用小于等于。
若求最小的解，那么初始时把 $ d[] $ 设为无穷小，用最长路求解。即 if $ (d[v]<d[u]+w(u,v)) $ 进行更新，而建图的时候也要用大于等于。
以求解最大的为例（最小解同理）$ d[s] $ 一开始为无穷大，图最短路更新的条件为： $ if(d[v]>d[u]+w(u,v))d[v]=d[u]+w(u,v) $ ; 通过不断的松弛，使得d的值不断变小，直到满足所有条件，也就是说满足条件的时候就是最大的了。
那么这题我们可以分情况讨论
1.当 $ x=1 $ 建边 $ w[i,j]=0 \ w[j,i]=0 $
2.当 $ x=2 $ 建边 $ w[i,j]=1( $ 如果 $ i=j $ 输出 $ -1 $
3.当 $ x=3 $ 建边 $ w[j,i]=0 $ 可以取等就取等
4.当 $ x=4 $ 建边 $ w[j,i]=1( $ 如果 $ i=j $ 输出 $ -1 $
5.当 $ x=5 $ 建边 $ w[i,j]=0 $ 可以取等就取等
最后从 $ 0 $ 号节点向各个节点连一条长度为 $ 1 $ 的边（至少一个糖果，跑spfa最长路即可。
对于环特判，spfa一个点进入队列的次数大于等于n次，则说明存在环
最后统计每个点的糖果数即可
注意
$ ans $ 开 $ long \ long $ 十年 $ OI $ 一场空，不开$ long \ long $见祖宗
从 $ 0 $ 号节点建图倒过来枚举（出题人卡 $ spfa $ 丧心病狂， $ spfa $ 的效率与建图有关所以反过来就起飞
代码
#include<bits/stdc++.h>
using namespace std;
const int size=200010;
int tot,head[size],ver[size*2],Next[2*size],edge[2*size];
int v[size],d[size],to[size],n,k;
bool flag=1;
long long ans;
queue<int>q;
void add(int x,int y,int z){
ver[++tot]=y;edge[tot]=z;Next[tot]=head[x];head[x]=tot;
}
void spfa(){
memset(d,0,sizeof(d));
memset(v,0,sizeof(v));
v[0]=1;d[0]=0;
q.push(0);
while(q.size()){
int x=q.front();
q.pop();v[x]=0;
if(to[x]==n-1){
printf("-1");
exit(0);
}to[x]++;
for(int i=head[x];i;i=Next[i]){
int y=ver[i],z=edge[i];
if(d[y]<d[x]+z){
d[y]=d[x]+z;
if(!v[y]) q.push(y),v[y]=1;
}
}
}
}
int main(){
scanf("%d %d",&n,&k);
while(k--){
int x,a,b;
scanf("%d %d %d",&x,&a,&b);
if(x==1){
add(a,b,0);add(b,a,0);
}else if(x==2){
if(a==b) flag=0;
add(a,b,1);
}else if(x==3){
add(b,a,0);
}else if(x==4){
if(a==b) flag=0;
add(b,a,1);
}else{
add(a,b,0);
}
if(!flag){
printf("-1");
return 0;
}
}
for(int i=n;i;--i) add(0,i,1);
spfa();
for(int i=1;i<=n;++i) ans+=d[i];
printf("%lld",ans);
return 0;
}
