hdu 5418 题解
第一眼看到这题,哇,这不是我刚做完的题吗?大水题!然后




这题表面很水,实际上有点坑。
题意
求经过 1−n(不能遗漏) 并且回到 1 的最短路。
在看这题之前我们可以来看下这题
最短Hamilton路
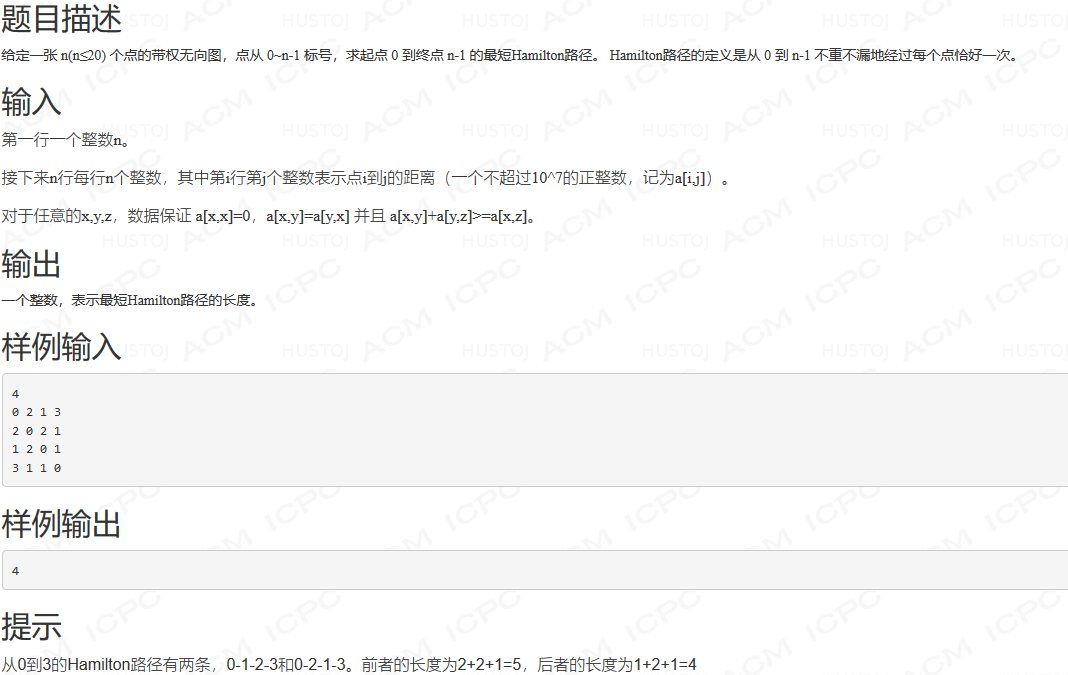
这道题的要求是我们要让每个点不重不漏的经过并且最终到达 n−1 我们看数据范围,就可以直接状压dp,枚举状态。
由于题目已经给出最短路,便可以直接计算
#include<bits/stdc++.h>
using namespace std;
int n,a[30][30];
int f[1100000][30];
int main(){
scanf("%d",&n);
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
scanf("%d",&a[i][j]);
}
}
memset(f,0x3f,sizeof(f));
f[1][0]=0;
for(int i=1;i<(1<<n);++i){//状态
for(int j=0;j<n;++j){//终点
if((i>>j)&1){
for(int k=0;k<n;++k){//起点
if(((i>>k)&1)&&a[j][k]){//保证有路相通
f[i][j]=min(f[i][j],f[i^(1<<j)][k]+a[k][j]);//找没能达到j的
}
}
}
}
}
printf("%d",f[(1<<n)-1][n-1]);//最后在n-1
return 0;
}
那么我们回到这题,它给出每个点的边,最后都要经过,并且返回,仔细一想,不就是多了个最短路吗?直接跑一遍 floyd 枚举终点返回不就好了?
然后我就写下了这个代码
#include<bits/stdc++.h>
using namespace std;
const int INF=1<<30;
int n,m,T,dis[20][20];
int f[(1<<20)][20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
if(n==1){
printf("0\n");
continue;
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(i==j) dis[i][j]=0;
else dis[i][j]=INF;
}
}
for(int i=1;i<=m;++i){
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
dis[x][y]=min(dis[x][y],z);
dis[y][x]=dis[x][y];
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
memset(f,0x3f,sizeof(f));
f[1][1]=0;
for(int i=1;i<(1<<n);++i){
for(int j=1;j<=n;++j){
if((i>>(j-1))&1){
for(int k=1;k<=n;++k){
if(((i>>(k-1))&1)&&(dis[j][k]!=INF)){
f[i][j]=min(f[i][j],f[i^(1<<(j-1))][k]+dis[j][k]);
}
}
}
}
}
int ans=1<<30;
for(int i=1;i<=n;++i){
ans=min(ans,f[(1<<n)-1][i]+dis[i][1]);
}printf("%d\n",ans);
}
return 0;
}
然后RE,后面问了乐老师,发现这个题会出现自环
if(n==1){
printf("0\n");
continue;
}
这个就是问题的关键所在,不能直接 continue 因为后面还有边没读进来,会导致RE。
然后我就这样写了一下
#include<bits/stdc++.h>
using namespace std;
const int INF=1<<30;
int n,m,T,dis[20][20];
int f[(1<<20)][20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
for(int i=0;i<=n;++i){
for(int j=0;j<=n;++j){
if(i==j) dis[i][j]=0;
else dis[i][j]=INF;
}
}
for(int i=1;i<=m;++i){
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
dis[x][y]=min(dis[x][y],z);
dis[y][x]=dis[x][y];
}
if(n==1){
printf("0");
continue;
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
memset(f,0x3f,sizeof(f));
f[1][1]=0;
for(int i=1;i<(1<<n);++i){
for(int j=1;j<=n;++j){
if((i>>(j-1))&1){
for(int k=1;k<=n;++k){
if(((i>>(k-1))&1)&&(dis[k][j]!=INF)){
f[i][j]=min(f[i][j],f[i^(1<<(j-1))][k]+dis[k][j]);
}
}
}
}
}
int ans=1<<30;
for(int i=1;i<=n;++i){
ans=min(ans,f[(1<<n)-1][i]+dis[i][1]);
}printf("%d\n",ans);
}
return 0;
}
听取 wa 声一片,后面自己看了下题解,觉得思路没问题,看着它把最大值都定义为 0x3f3f3f3f 我就一改,然后它过了??
原因是两个最大值不一样导致 dp 过程中会出现错误,最后我改成了
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int n,m,T,dis[20][20];
int f[(1<<20)][20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d %d",&n,&m);
for(int i=0;i<=n;++i){
for(int j=0;j<=n;++j){
if(i==j) dis[i][j]=0;
else dis[i][j]=INF;
}
}
for(int i=1;i<=m;++i){
int x,y,z;
scanf("%d %d %d",&x,&y,&z);
dis[x][y]=min(dis[x][y],z);
dis[y][x]=dis[x][y];
}
if(n==1){
printf("0\n");
continue;
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
if(dis[i][j]>dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
}
}
}
memset(f,0x3f,sizeof(f));
f[1][1]=0;
for(int i=1;i<(1<<n);++i){
for(int j=1;j<=n;++j){
if((i>>(j-1))&1){
for(int k=1;k<=n;++k){
if(((i>>(k-1))&1)&&(dis[k][j]!=INF)){
f[i][j]=min(f[i][j],f[i^(1<<(j-1))][k]+dis[k][j]);
}
}
}
}
}
int ans=INF;
for(int i=1;i<=n;++i){
ans=min(ans,f[(1<<n)-1][i]+dis[i][1]);
}printf("%d\n",ans);
}
return 0;
}
然后终于 AC,其实这道题本身不难,主要是在一些细节上的处理,在多组数据下暴露的很明显,平时写题细节方面还是要多多注意。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 智能桌面机器人:用.NET IoT库控制舵机并多方法播放表情
· Linux glibc自带哈希表的用例及性能测试
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 手把手教你在本地部署DeepSeek R1,搭建web-ui ,建议收藏!
· 新年开篇:在本地部署DeepSeek大模型实现联网增强的AI应用
· Janus Pro:DeepSeek 开源革新,多模态 AI 的未来
· 互联网不景气了那就玩玩嵌入式吧,用纯.NET开发并制作一个智能桌面机器人(三):用.NET IoT库
· 【非技术】说说2024年我都干了些啥