2019.8.18小结
T1 邮递员送信 100/100
题意
有一个邮递员要送东西,邮局在结点1。他总共要送N-1样东西,其目的地分别是2~N。由于这个城市的交通比较繁忙,因此所有的道路都是单行的,共有M条道路,通过每条道路需要一定的时间。这个邮递员每次只能带一样东西。求送完这N-1样东西并且最终回到邮局最少需要多少时间。
很容易发现我们要求 \(\sum_{j=1}^n\) dis[1][ j ]+dis[ j ][1],可以想到跑spfa,对于dis[1][ j ]可以一遍spfa解决但是对于 dis[ j ][1]却不好解决,如果跑n遍spfa明显超时,但我们可以换个思路,建立反图,对节点1跑spfa,那么1节点到别的点的距离就是别的点到1节点的距离。
代码
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
const int N=1010,M=100010;
int head[N][2],ver[M][2],edge[M][2],Next[M][2],d[N][2];
int n,m,tot1,tot2;
long long ans;
bool v[N];
queue<int> q;
void add(int x,int y,int z){
ver[++tot1][0]=y;edge[tot1][0]=z;Next[tot1][0]=head[x][0],head[x][0]=tot1;
}
void add1(int x,int y,int z){
ver[++tot2][1]=y;edge[tot2][1]=z;Next[tot2][1]=head[x][1],head[x][1]=tot2;
}
void spfa(){
memset(d,0x3f,sizeof(d));
d[1][0]=0,v[1]=1;
q.push(1);
while(q.size()){
int x=q.front();q.pop();
v[x]=0;
for(int i=head[x][0];i;i=Next[i][0]){
int y=ver[i][0],z=edge[i][0];
if(d[y][0]>d[x][0]+z){
d[y][0]=d[x][0]+z;
if(!v[y]) q.push(y),v[y]=1;
}
}
}
while(!q.empty()) q.pop();
memset(v,0,sizeof(v));
d[1][1]=0,v[1]=1;
q.push(1);
while(q.size()){
int x=q.front();q.pop();
v[x]=0;
for(int i=head[x][1];i;i=Next[i][1]){
int y=ver[i][1],z=edge[i][1];
if(d[y][1]>d[x][1]+z){
d[y][1]=d[x][1]+z;
if(!v[y]) q.push(y),v[y]=1;
}
}
}
}
int main(){
n=read();m=read();
for(int i=1;i<=m;++i){
int x,y,z;
x=read();y=read();z=read();
add(x,y,z);
add1(y,x,z);
}
spfa();
for(int i=1;i<=n;++i){
ans+=d[i][0]+d[i][1];
}
printf("%lld",ans);
return 0;
}
T2 敲砖块 70/100
题意
在一个凹槽中放置了N层砖块,最上面的一层油N块砖,从上到下每层一次减少一块砖。每块砖都有一个分值,敲掉这块砖就能得到相应的分值,如图所示。
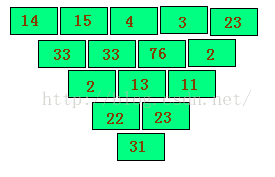
如果你想敲掉第i层的第j块砖的话,若i=1,你可以直接敲掉它;若i>1,则你必须先敲掉第i-1层的第j和第j+1块砖。
你现在可以敲掉最多M块砖,求得分最多能有多少。
一道dp题,一开始想到的是一行一行dp然而发现,选[ i , j ]就要选[ i-1 , j+1]和[ i ,j ]上面所有的方块,似乎不满足无后效性,那怎么办呢?
我们发现输入文件时这样的
4 5
2 2 3 4
8 2 7
2 3
49
我们可以去思考是不是可以一列一列dp,从n列向1列dp这样就没有后效性了,我们可以定义状态f[i][j][k]表示当前在第i列选了j个,总共选了k个,状态转移方程为
f[i][j][k]=max(f[i+1][t][k-j]+s[i][j],f[i][j][k])
t>=j-1&&t<=n-i
s[i][j]表示第j列前i个的和
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,ans,f[55][55][3000],a[55][55],s[55][55];
int main(){
scanf("%d %d",&n,&m);
memset(f,-0x3f,sizeof(f));
f[n+1][0][0]=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=n-i+1;++j){
scanf("%d",&a[i][j]);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n-i+1;++j){
s[j][i]=s[j][i-1]+a[i][j];
}
}
for(int i=n;i>=1;--i){
for(int j=0;j<=n-i+1;++j){
for(int k=j;k<=m;++k){
for(int t=max(j-1,0);t<=n-i;++t){
f[i][j][k]=max(f[i+1][t][k-j]+s[i][j],f[i][j][k]);
}
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n-i+1;++j){
ans=max(ans,f[i][j][m]);
}
}
printf("%d",ans);
return 0;
}
T3 等价表达式 30/0
题意
给一个表达式然后再给n个表达式,判断是否等价
一道大模拟题,将a带为数,并且取模防止溢出
#include<bits/stdc++.h>
using namespace std;
const int mod=10007;
char w[55],c[55];
int a[100],t1,t2,x,n;
long long ans[5],c1[55],c2[55],c3[55];
int power(int x,int y){
int tmp=1;
while(y){
if(y&1) tmp=(tmp*x)%mod;
x=(x*x)%mod;
y>>=1;
}
return tmp%mod;
}
void clu(){
int m1=c1[t2],n1=c1[t2-1],m2=c2[t2],n2=c2[t2-1],m3=c3[t2],n3=c3[--t2];
switch(w[t1--]){
case '+':c1[t2]=(n1+m1+mod)%mod; c2[t2]=(n2+m2+mod)%mod; c3[t2]=(n3+m3+mod)%mod; break;
case '-':c1[t2]=(n1-m1+mod)%mod; c2[t2]=(n2-m2+mod)%mod; c3[t2]=(n3-m3+mod)%mod; break;
case '*':c1[t2]=(n1*m1+mod)%mod; c2[t2]=(n2*m2+mod)%mod; c3[t2]=(n3*m3+mod)%mod; break;
case '^':c1[t2]=power(n1,m1); c2[t2]=power(n2,m2); c3[t2]=power(n3,m3); break;
}
}
void js(){
x=0;
for(int i=0;i<strlen(c);i++){
if(c[i]=='a') {c1[++t2]=3;c2[t2]=7;c3[t2]=13;}
else if(isdigit(c[i])) x=x*10+c[i]-'0';
else{
if(x!=0){c1[++t2]=x;c2[t2]=x;c3[t2]=x;x=0;}
if(a[c[i]]==0)continue;
if(c[i]=='('||t1==0&&c[i]!=')') w[++t1]=c[i];
else{
if(a[c[i]]<a[w[t1]]){
if(c[i]!=')') w[++t1]=c[i];
else{
while(w[t1]!='('&&t1) clu();
if(w[t1]=='(')t1--;
}
}
else{
while(a[c[i]]>=a[w[t1]]&&t1) clu();
if(c[i]!=')') w[++t1]=c[i];
}
}
}
}
if(x!=0){c1[++t2]=x;c2[t2]=x;c3[t2]=x;x=0;}
while (t1)clu();
}
int main(){
a['(']=5;a[')']=1;a['^']=2;a['*']=a['/']=3;a['+']=a['-']=4;
gets(c);
scanf("%d",&n);
js();
gets(c);
ans[1]=c1[1];ans[2]=c2[1];ans[3]=c3[1];
for(int i=1;i<=n;++i){
t1=t2=0;gets(c);js();
if(ans[1]==c1[1]%mod&&ans[2]==c2[1]%mod&&ans[3]==c3[1]%mod)
printf("%c",i+64);
}
return 0;
}
T4 扩散 100/100
题意
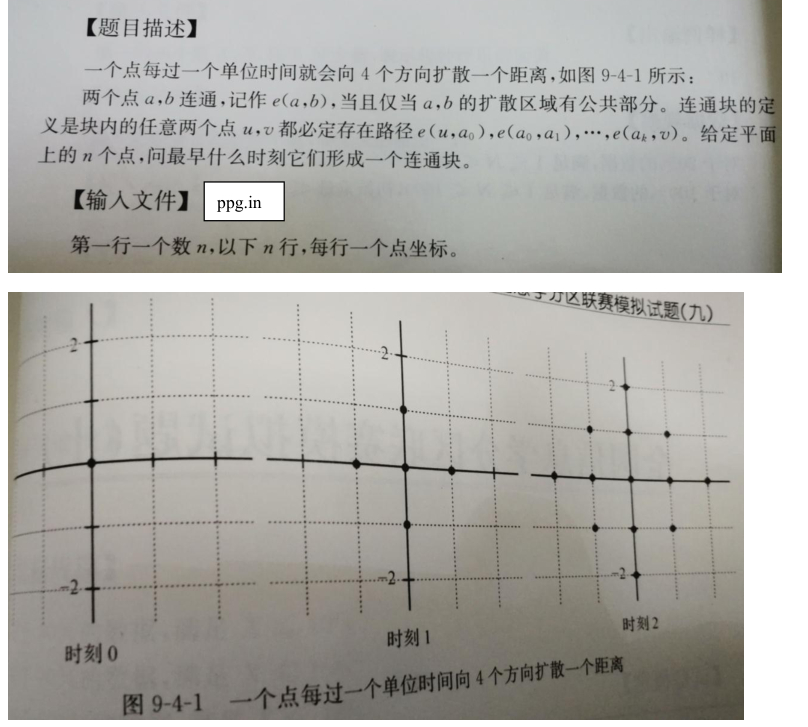
先讲一下一种容易陷入误区错误思路
要使时间最小,就去找相对于每个点的最短曼哈顿距离,然后取最大值,时间就是(maxn+1)/2。
代码
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<iostream>
#define ll long long
#define MX 55
using namespace std;
int d[MX][MX];
int x[MX],y[MX];
int ans=0;
int man=1<<30;
int n;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d %d",&x[i],&y[i]);
}
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
d[i][j]=d[j][i]=(abs(x[i]-x[j])+abs(y[i]-y[j]));
}
}
for(int i=1;i<=n;++i){
man=1<<30;
for(int j=1;j<=n;++j){
if(i==j) continue;
man=min(d[i][j],man);
}
ans=max(ans,man);
}
printf("%d",(ans+1)/2);
return 0;
}
这样做只有20分,为什么错了?
因为每次取最小的会使你遗漏边,有些边是一定要选的却没选,不选的话会导致联通块不连通,举个例子吧
如果按照上面的方法就只会选到红边,但黑边至少要选一条,这就会导致联通块不连通,所以错误了。
正解
一种比较巧妙的方法,可以看作在最长距离中找一个最短的曼哈顿距离便可以二分,判断联通可以用并查集或者bfs。
代码
#include<bits/stdc++.h>
using namespace std;
int n,ans,l,r,cnt,fa[60],zx[60],zy[60];
int find(int x){
if(x==fa[x]) return x;
else return fa[x]=find(fa[x]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d %d",&zx[i],&zy[i]);
}
l=0,r=1e9;
while(l<=r){
int mid=(l+r)>>1;
for(int i=1;i<=n;++i){
fa[i]=i;
}
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
int dis=abs(zx[i]-zx[j])+abs(zy[i]-zy[j]);
if(dis<=mid*2){
int fa1=find(i);
int fa2=find(j);
if(fa1!=fa2) fa[fa1]=fa2;
}
}
}
cnt=0;
for(int i=1;i<=n;++i){
if(fa[i]==i) cnt++;
}
if(cnt==1) r=mid-1;
else l=mid+1;
}
printf("%d",l);
return 0;
}
另外这道题还可以计算出任意两点间联通的时间,然后求最小生成树(MST),则MST的最大边就是答案。因为MST的性质之一就是满足任意两点间的最大边权最小。
总结,今天考试总体还行,等价表达式调了好久,不知道getline怎么用。。。对于模拟还是不熟,练的太少了,代码能力不强,要多写点这种题。


