洛谷 P4206 [NOI2005]聪聪与可可 题解

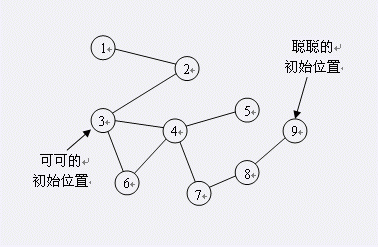
题面

输入

数据的第1行为两个整数N和E，以空格分隔，分别表示森林中的景点数和连接相邻景点的路的条数。 第2行包含两个整数C和M，以空格分隔，分别表示初始时聪聪和可可所在的景点的编号。 接下来E行，每行两个整数，第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。 所有的路都是无向的，即：如果能从A走到B，就可以从B走到A。 输入保证任何两个景点之间不会有多于一条路直接相连，且聪聪和可可之间必有路直接或间接的相连。

输出

输出1个实数，四舍五入保留三位小数，表示平均多少个时间单位后聪聪会把可可吃掉。

样例输入

4 3
1 4
1 2
2 3
3 4

样例输出

1.500

样例说明

开始时，聪聪和可可分别在景点1和景点4。

第一个时刻，聪聪先走，她向更靠近可可(景点4)的景点走动，走到景点2，然后走到景点3；假定忽略走路所花时间。

可可后走，有两种可能：

第一种是走到景点3，这样聪聪和可可到达同一个景点，可可被吃掉，步数为1，概率为 。

第二种是停在景点4，不被吃掉。概率为 。

到第二个时刻，聪聪向更靠近可可(景点4)的景点走动，只需要走一步即和可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。

所以平均的步数是1* +2* =1.5步。

分析题目，这道题有两个难点。

一.猫走一步和两步它所付出的代价是相同的，但怎么去判它何时走一步何时走两步？

我们bfs预处理求得每一个点对的距离即可

二.状态怎么去定义

由于猫走的步数与猫的位置以及老鼠位置有关，所以我们可以去定义f[i][j]表示当猫在i,老鼠在j时的期望值。

我们可以得到边界条件

如果猫和老鼠在同一处即(i=j)那么猫的步数显然为0,f[i][j]=0;

由于猫走一步与两步的代价是相同的那么f[i][j]=1;

其余情况f[i][j]=\(\sum\)(f[two][k]/p[j]+1) +1

two是猫走两步能到达的点,k表示老鼠所能去的点,p[j]表示该节点的出度(+1表示包括该节点,)求和之后再加一表示步数增加一步。最后的答案就是f[c][m]

代码

#include<bits/stdc++.h> 
using namespace std;
int n,e,c,m,u,v;
int head[1005],Next[2005],ver[2005],tot,degree[1005];
int x[1005][1005],dis[1005][1005];
double f[1005][1005];
void add(int x,int y){
	ver[++tot]=y;Next[tot]=head[x];head[x]=tot,++degree[x];
}
void bfs(){
	for(int i=1;i<=n;++i){
		queue<int> q;
		q.push(i);
		dis[i][i]=0;
		while(!q.empty()){
			int from=q.front();
			q.pop();
			for(int j=head[from];j;j=Next[j]){
				int y=ver[j];
				if(dis[i][y]==-1){
					dis[i][y]=dis[i][from]+1;
					q.push(y);
				}
			}
		}
	}
}
double dp(int i,int j){
	if(f[i][j]!=-1.0) return f[i][j];
	if(i==j) return f[i][j]=0.0;
	if(x[i][j]==j) return f[i][j]=1.0;
	if(x[x[i][j]][j]==j) return f[i][j]=1.0;
	f[i][j]=0.0;
	for(int k=head[j];k;k=Next[k]){
		int y=ver[k];
		f[i][j]+=dp(x[x[i][j]][j],y);
	}
	f[i][j]=(f[i][j]+dp(x[x[i][j]][j],j))/(double)(degree[j]+1)+1;
	return f[i][j];
}
int main(){
	scanf("%d %d %d %d",&n,&e,&c,&m);
	while(e--){
		scanf("%d %d",&u,&v);
		add(u,v);
		add(v,u);
	}
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			f[i][j]=-1.0;
		}
	}
	memset(dis,-1,sizeof(dis));
	bfs();
	memset(x,0x3f,sizeof(x));
	for(int from=1;from<=n;++from){
		for(int i=head[from];i;i=Next[i]){
			int y=ver[i];
			for(int j=1;j<=n;++j){
				if(dis[from][j]==dis[y][j]+1 && x[from][j]>y){
					x[from][j]=y;
				}
			}
		}
	}
	printf("%.3lf",dp(c,m));
	return 0;
}