原码、反码、补码、移码

原码、反码、补码、移码

背景：为了解决计算机中减法计算的问题，因为计算机中只有加法器，减法的计算是要转换成加法才能进行。

原码

二进制首位为标志位

正数 标志位为0

0	x	x	x	x	x	x	x

负数 标志位为1

1	x	x	x	x	x	x	x

示例：

14 = 00001110

-21 = 10010101

反码

正数：原码、反码、补码相同，为原码本身。

负数：原码 -> 反码：标志位（也就是符号位）不变，其他取反

14 ： 0000 1110

-21： 1110 1010 计算方法如下

-21原码：10010101
取反：   11101010

补码

补码在反码的基础上加1，符号位保持不变

补码 = 反码 + 1

-21 = 1110 1011

移码

我们都知道正数的原码、反码、补码相同，为原码本身，但是移码是在补码的基础上符号位取反的。

负数的移码是在其补码的基础上符号位取反的来的。

移码 = 补码符号位取反

总的来说，移码是在补码的基础上，符号位取反得来的。

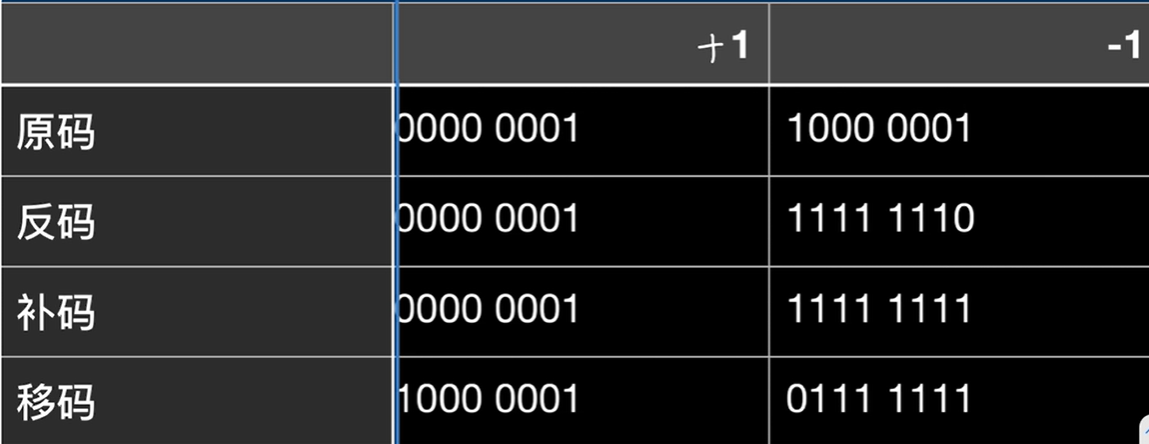
示例：

-21的移码：

-21 = 0110 1011

计算机内计算方式

示例1：

14 + (-21) = -7 （11111011就是-7的补码）

采用的是 补码 + 补码 的方式

最后将 补码 -> 反码 -> 原码

示例2：

14-（-21）= 14 + 21 = 35

知识点补充与总结

(1)8位二进制数能表示的十进制数范围为-128到+127

(2)如果数小于-128或大于127,则会溢出，溢出只能用两个字节，16位二进制数表示了
(3)0的补码为00000000,-128的补码为10000000:
(4)计算机中有符号数用补码表示
(5)原码首位为标志位，1表示负数，0表示正数:
(6)反码 = 原码的标志位不变，其他取反
(7)补码=反码 + 1;
(8)正整数的原码、反码、补码相同