计算机中的基本运算

二进制的算术运算

1.二进制的加法运算

示例：

0+0=0  0+1=1 1+0=1  1+1=10

1011+1001=10100

2，二进制的减法运算

示例：

1-1=0 1-0=1 0-0=0 0-1=1(解释一下这个，可以看作是向前借 1，看作 2-1)

1101-1010=0011(当然前面的0 是可以省略的)

3.二进制的乘法运算

示例:

101X11=1111

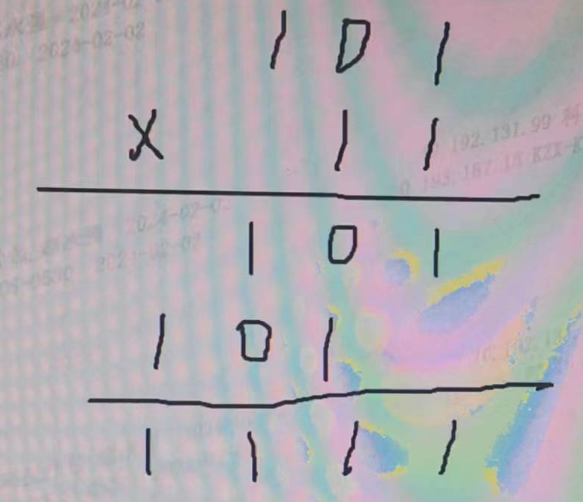
4.二进制的除法运算

示例:

11001/101=101

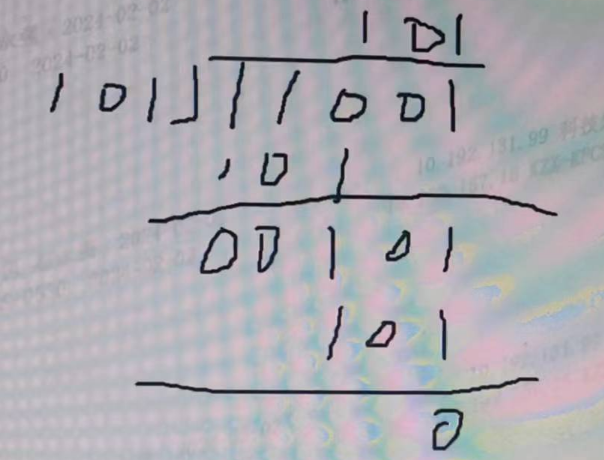
二进制的逻辑运算

1.逻辑与运算 (And )

1&1=1 0&1=0
1&0=0 0&0=0
同时为 1，结果为 1，任意一方为 0，则结果为0
1010&1101=1000

2.逻辑或运算 (or)

I if(AllB)
1&1=1 0&1=1
1&0=1 0&0=0
任意一方为 1，则结果为 1,双方都为 0，则结果为 0.
1010&1101=1111

3.逻辑非运算

! 1=0 ! 0=1
! 1001=0110

4.异或运算(XOR)

^ XOR
相同癖矿为 0，不同为1
1010^1110=0100

5.同或运算 (XNOR)

XNOR
相同为 1，不同为0

1010 XNOR 1110=1011

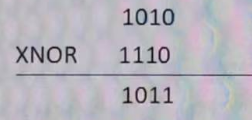
程序中一般没有同或运算符，两个数的异或结果再次异或 1，即可得到两个数的同或结果1010 XNOR 1110 = 1011

移位运算

移位运算:在数的二进制形式的基础上进行位移。
在很多计算机语言中都有移位运算。例如 c语言、Java
移位运算符:
<<左移运算

>>有符号右移 >>>无符号右移

下面举例子讲解:

1.左移运算

左移运算:相当于是乘法运算，m<<n=m*2^n

-26<<1
负数在计算机中以补码的形式存储

-26 原码=10011010

-26 补码=11100110
将他的补码左移一位为(相当于将前面的 1 给移没了) :

将其转换成原码=10110100 就是十进制的-52，由此-26<<1=-52

2.有符号右移

26>>1=13
13>>1=6
正数右移:左侧补 0 负数右移: 左侧补 1
左移运算:相当于除法运算
m>>n = m /2^n
注意: 结果有小数的时候，小数部分会被舍弃
例如: -26>>1=-13

3.无符号右移

26>>>1
正数右移:左侧补 0
负数右移:左侧补0
27>>1
正数右移:左侧补 0
负数右移:左侧补 1