机器学习常见模型以及代码实现

1.性能度量

1.1 简介

一个机器学习模型需要一些性能度量指标来判断它的好坏，了解各种评估的方法优点和缺点，在实际应用中选择正确的评估方法是十分重要的。

对于分类模型的各种性能度量的算法，如准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值等，接下来我们将详细的说明这些行性能度量算法。

1.2 代码示例

from sklearn.metrics import precision_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
y_true=[1,0,1,1,0] #样本实际值
y_pred=[1,0,1,0,0] #模型预测值
res=precision_score(y_true,y_pred,average=None) #准确率
#[0.66666667    1. ] 分别是正例和反例的预测准确率，2/3与2/2
print(res)
res=confusion_matrix(y_true,y_pred) # 混淆矩阵
print(res)
# [[2 0]
#  [1 2]]
res=classification_report(y_true,y_pred) #分类报告，获取更多详细的内容
print(res)

#k折交叉验证法
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris #导入鸢尾花数据集
from sklearn.svm import SVC
iris=load_iris()
clf=SVC(kernel='linear',C=1) #构建支持向量机模型
scores=cross_val_score(clf,iris.data,iris.target,cv=5)
print(scores)

2.线性回归—波士顿房价

1.1 概念

机器学习中的两个常见的问题：回归任务和分类任务。那什么是回归任务和分类任务呢？简单的来说，在监督学习中（也就是有标签的数据中），标签值为连续值时是回归任务，标志值是离散值时是分类任务。而线性回归模型就是处理回归任务的最基础的模型。

线性：两个变量之间的关系是一次函数关系的——图象是直线，叫做线性；

非线性：两个变量之间的关系不是一次函数关系的——图象不是直线，叫做非线性。

回归：人们在测量事物的时候因为客观条件所限，求得的都是测量值，而不是事物真实的值，为了能够得到真实值，无限次的进行测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来。

1.2 解决的问题

对大量的观测数据进行处理，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在，从而就可以模拟出结果，也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如：对房价的预测、判断信用评价、电影票房预估等。

1.3 基本形式

在只有一个变量的情况下，线性回归可以用方程：y = ax+b 表示。而如果有多个变量，也就是n元线性回归的形式如下：

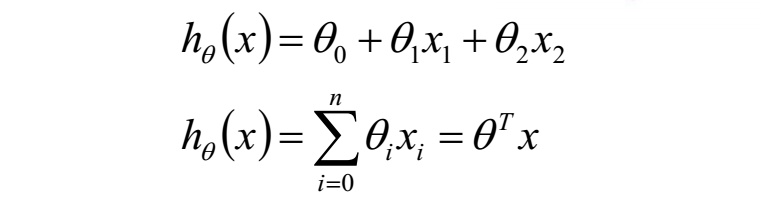
1.4 回归分析代码实现

from sklearn.linear_model import LinearRegression

clf=LinearRegression()
clf.fit([[0,0],[1,1],[2,2]],[0,1,2]) #模型训练
'''
y=0.5*x1+0.5*x2
'''
pre=clf.predict([[3,3]]) #模型预测
clf.coef_
clf.intercept_
print(pre)

1.5 波士顿房价回归分析

#波士顿房价数据回归分析
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
bosten=load_boston() #实例化
x=bosten.data[:,5:6]

clf=LinearRegression()
clf.fit(x,bosten.target) #模型训练
clf.coef_ #回归系数
y_pre=clf.predict(x) #模型输出值

plt.scatter(x,bosten.target) #样本实际分布
plt.plot(x,y_pre,color='red') #绘制拟合曲线
plt.show()

1.6 研究生录取概率预测

import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

data=pd.read_csv('LogisticRegression.csv')
data_tr,data_te,label_tr,label_te=train_test_split(data.iloc[:,1:],data['admit'],test_size=0.2)
clf=LogisticRegression()
clf.fit(data_tr,label_tr)
pre=clf.predict(data_te)
res=classification_report(label_te,pre)
print(res)

3.决策树—泰坦尼克号生还预测

3.1 泰坦尼克号生还预测

泰坦尼克号沉没是历史上最臭名昭着的沉船之⼀。 1912年4⽉ 15⽇，在她的处⼥航中，泰坦尼克号在与冰⼭相撞后沉没，在2224名乘客和机组⼈员中造成1502⼈死亡。这场耸⼈听闻的悲剧震惊了国际社会，并为船舶制定了更好的安全规定。造成海难失事的原因之⼀是乘客和机组⼈员没有⾜够的救⽣艇。尽管幸存下沉有⼀些运⽓因素，但有些⼈⽐其他⼈更容易⽣存，例如妇⼥，⼉童和上流社会。在这个案例中，我们要求您完成对哪些⼈可能存活的分析。特别是，我们要求您运⽤机器学习⼯具来预测哪些乘客幸免于悲剧。

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
data=pd.read_csv('titanic_data.csv')
print(data)
data.drop('PassengerId',axis=1,inplace=True) #删除PassengerId列

data.loc[data['Sex']=='male','Sex']=1
data.loc[data['Sex']=='female','Sex']=0 #用数值1来代替male 用数值0来代替female

data.fillna(data['Age'].mean(),inplace=True) #用均值来填充缺失值

Dtc=DecisionTreeClassifier(max_depth=5,random_state=8) #构建决策树模型
Dtc.fit(data.iloc[:,1:],data['Survived']) #模型训练
pre=Dtc.predict(data.iloc[:,1:]) #模型预测
pre==data['Survived'] #比较模型预测值与样本实际值是否一致
classification_report(data['Survived'],pre) #模型分类报告
print(classification_report(data['Survived'],pre) )

4.朴素贝叶斯—鸢尾花分类

朴素贝叶斯算法（Naive Bayesian algorithm) 是应用最为广泛的分类算法之一。

朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化，即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重，也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果，但是在实际的应用场景中，极大地简化了贝叶斯方法的复杂性。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB

X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
acc=sum(y_pred==y_test)/len(y_pred)
print(acc)

5.聚类算法—鸢尾花分类

聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

5.1 K-Means聚类数据

from sklearn.datasets import load_iris
import numpy as np

iris = load_iris()
data = iris.data
n = len(data)
k = 2
dist = np.zeros([n, k+1])
# 1、选中心
center = data[:k, :]
center_new = np.zeros([k, data.shape[1]])
while True:
    # 2、求距离
    for i in range(n):
        for j in range(k):
            dist[i, j] = np.sqrt(sum((data[i, :] - center[j, :])**2))
        dist[i, k] = np.argmin(dist[i, :k])   # 3、归类

    for i in range(k):   # 4、求新类中心
        index = dist[:, k] == i
        center_new[i, :] = data[index, :].mean(axis=0)

    if np.all(center == center_new):   # 5、判定结束
        break
    center = center_new

5.2 调用sklearn实现聚类分析

from sklearn.datasets import load_iris
from sklearn.cluster import KMeans

iris = load_iris()

model = KMeans(n_clusters=3).fit(iris.data)

print(model.labels_)

6.最近邻算法—鸢尾花分类

kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数数以一个类型别，则该样本也属于这个类别，并具有该类别上样本的特征。该方法在确定分类决策上，只依据最近邻的一个或者几个样本的类别来决定待分样本所属的类别。

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

iris=load_iris()
data_tr,data_te,label_tr,label_te=train_test_split(iris.data,iris.target,test_size=0.2) #拆分专家样本集


model=KNeighborsClassifier(n_neighbors=50) #构建模型
model.fit(data_tr,label_tr) #模型训练
pre=model.predict(data_te) #模型预测
acc=model.score(data_te,label_te) #模型在测试集上的精度
print(acc)

7.支持向量机—鸢尾花分类

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

from sklearn.datasets import load_iris
from sklearn.svm import LinearSVC
from sklearn.model_selection import train_test_split

iris = load_iris()

data_tr, data_te, label_tr, label_te = train_test_split(iris.data, iris.target, test_size=0.2)
model = LinearSVC(dual=False).fit(data_tr, label_tr)
pre = model.predict(data_te)
acc_te = sum(pre == label_te)/len(pre)

8.人工神经网络

人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。它是在现代神经科学研究成果的基础上提出的，试图通过模拟大脑神经网络处理、记忆信息的方式进行信息处理。

8.1 运用sklearn库构建人工神经网络

from sklearn.neural_network import MLPRegressor
import pandas as pd
import numpy as np

#调用sklearn实现神经网络算法
data_tr=pd.read_csv('BPdata_tr.txt') #训练集样本
data_te=pd.read_csv('BPdata_te.txt') #测试集样本

print(data_tr.iloc[:,:2])

model=MLPRegressor(hidden_layer_sizes=(10,),random_state=10,max_iter=800,learning_rate_init=0.3) #构建模型
model.fit(data_tr.iloc[:,:2],data_tr.iloc[:,2]) #模型训练
pre=model.predict(data_te.iloc[:,:2]) #模型预测
err=np.abs(pre-data_te.iloc[:,2]).mean() #模型预测误差
print(err)

8.2 不掉库构建人工神经网络

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x): #网络激活函数
    return 1/(1+np.exp(-x))

data_tr=pd.read_csv('BPdata_tr.txt') #训练集样本
data_te=pd.read_csv('BPdata_te.txt') #测试集样本

yita=0.85
#网络结构搭建
out_in=np.array([0.0,0,0,0,-1]) # 输出层的输入


w_mid=np.zeros([3,4]) #隐层神经元的权值&阈值
w_out=np.zeros([5]) #输出层神经元的权值&阈值

delta_w_out=np.zeros([5]) #输出层权值&阈值的修正量
delta_w_mid=np.zeros([3,4]) #中间层权值&阈值的修正量
#便于绘制误差变化
err=[]

for j in range(1000): #控制训练轮数
    error=[]
    for it in range(500):
        net_in = np.array([data_tr.iloc[it,0],data_tr.iloc[it,1], -1])  # 网络输入
        real = data_tr.iloc[it,2]
        for i in range(4):
            out_in[i]=sigmoid(sum(net_in*w_mid[:,i])) #从输入到隐层的传输过程

        res=sigmoid(sum(out_in*w_out)) #模型预测值
        error.append(abs(real-res))

        print(it,'个样本训练的模型输出',res,'real',real)

        delta_w_out=yita*res*(1-res)*(real-res)*out_in #输出层权值的修正量
        delta_w_out[4]=-yita*res*(1-res)*(real-res) #输出层阈值的修正量
        w_out=w_out+delta_w_out

        for i in range(4):
            delta_w_mid[:,i]=yita*out_in[i]*(1-out_in[i])*w_out[i]*res*(1-res)*(real-res)*net_in #中间层神经元的权值修正量
            delta_w_mid[2, i] = -yita * out_in[i] * (1 - out_in[i]) * w_out[i] * res * (1 - res) * (real - res) #中间层神经元的阈值修正量
        w_mid=w_mid+delta_w_mid #更新
    err.append(np.mean(error))
plt.plot(err) #绘制误差变化线
plt.show()
plt.close()

#将测试集样本放入训练好的网络中去
error_te = []
for it in range(len(data_te)):
    net_in = np.array([data_te.iloc[it, 0], data_te.iloc[it, 1], -1])  # 网络输入
    real = data_te.iloc[it, 2]
    for i in range(4):
        out_in[i] = sigmoid(sum(net_in * w_mid[:, i]))  # 从输入到隐层的传输过程

    res = sigmoid(sum(out_in * w_out))  # 模型预测值
    error_te.append(abs(real - res))
plt.plot(error_te) #绘制误差变化线
plt.show()