数据结构——查找
1 查找
根据给定的值,在查找表中确定一个其关键字等于给定值的数据元素
查找表:由同一类数据元素构成的集合
静态查找表:只做查找操作的查找表
动态查找表:在查找过程中,还可以进行插入或删除操作的查找表
关键字:数据元素中某个数据项的值
主关键字:可以唯一标识一个记录的关键字
次关键字:可以标识多个记录的关键字
2 循序查找表
从表的第一个数据元素开始,逐个将数据元素的关键值与给定值相比较,若相等则表示查找到了,若不相等则表示没有找到;
/* 查找数组a中,与key值相等的元素,并返回数组元素的下标 */ int seqSearch(int a[],int n,int key) { for(int i=0;i<n;i++) { if(a[i]==key) return i; } return -1; }
3 折半查找表
被查找的表的数据元素必须是升序或者降序的有序表;取中间数据元素的关键字与给定值比较;若相等则表示查找到了;若给定值大,则在中间到最后元素这一半中再取中间元素的关键字与给定值比较;若给定值小,则在第一个到中间元素这一半中再取中间元素的关键字与给定值比较;依次类推,直到找到或者没找着;
/* 查找数组a中,与key值相等的元素,并返回数组元素 */ int binSearch(int a[],int n,int key) { int low=0; int high=n-1; int mid; while(low<=high) { mid=(low+high)/2; if(a[mid]==key) return mid; else if(a[mid]<key) low=mid+1; else high=mid-1; } return -1; }
4 插值查找
是对折半查找法的改进;主要应用于关键字分布比较均匀的有序表,而对不均匀的表不适用
/* 查找数组a中,与key值相等的元素,并返回数组元素 */ int binSearch(int a[],int n,int key) { int low=0; int high=n-1; int mid; while(low<=high) { mid=low+(key-a[low])/(a[high]-a[low])*(high-low); if(a[mid]==key) return mid; else if(a[mid]<key) low=mid+1; else high=mid-1; } return -1; }
5 斐波那契查找
是对折半查找法的改进;利用黄金分割点进行数据的分割;
/* 查找数组a中,与key值相等的元素,并返回数组元素 */ int fib[10]={1,1,2,3,5,8,13,21,34,55}; int fibSearch(int a[],int n,int key) { int low=0; int high=n-1; int k=0; while(n>fib[k]-1) k++; while(low<=high) { mid=low+fib[k-1]-1; if(a[mid]==key) { if(mid<n) return mid; else return n-1; } else if(a[mid]<key) { low=mid+1; k=k-2; } else { high=mid-1; k=k-1; } } return -1; } void main() { int a[]={7,18,23,39,46,55,62,71,84,98}; fibSearch(a,10,23); }
6 线性索引查找
索引是指将关键字从数据元素中独立出来,形成查找表;索引的作用是加快查找速度;索引由若干个索引项(由关键字和其对应记录的存储位置构成的一种数据结构)构成;
索引分类;
线性索引、树形索引、多级索引
线性索引:索引项是线性表的索引,包括稠密索引、分块索引、倒排索引
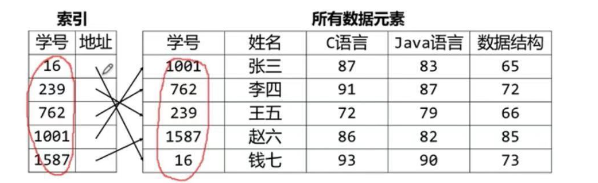
稠密索引:
索引项由关键字和地址构成;索引项的关键字是有序的,索引项的关键字可以使一个数据元素中的任何一项;当需要在所有数据元素中查找某一个时,可以使用有序查找法在索引项中通过关键字查找找到该数据元素。
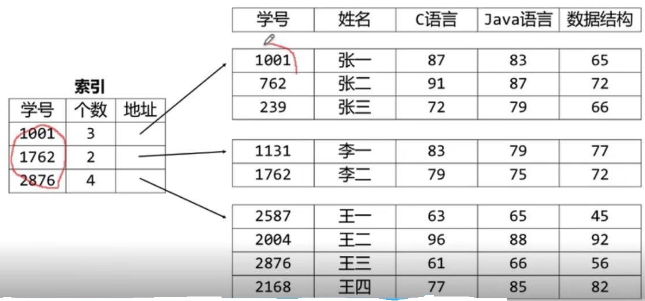
分块索引:
索引项由块中最大关键字、块中元素个数和块首地址构成;索引项中的关键字是有序的,块中数据元素不要求有序;索引项中的关键字可以使数据元素中的任何一项;当需要在所有元素中查找某一个时,首先使用有序查找法在索引项中通过关键字查找到该元素所在的块,然后使用其它查找法在块中找到该数据元素。
倒排索引:
索引项由次关键字、记录号构成;索引项中的次关键字是有序的;
| 1 | we should live by our own principles |
| 2 | they will live forver in our hearts |
| 3 | he hated to live a lie |
| 次关键字 | 记录号 |
| we | 1 |
| should | 1 |
| live | 1、2、3 |
| by | 1 |
| our | 1、2 |
| own | 1 |
| principles | 1 |
| they | 2 |
| will | 2 |
| forver | 2 |
| in | 2 |
| heart | 2 |
| he | 3 |
| hated | 3 |
| to | 3 |
| a | 3 |
| lie | 3 |
7 二叉排序树
可以使一棵空树;若左子树存在,则左子树的所有结点的值均小于根结点的值;若右子树存在,则右子树的所有结点的值均大于根结点的值;左右子树也是一棵二叉排序树;
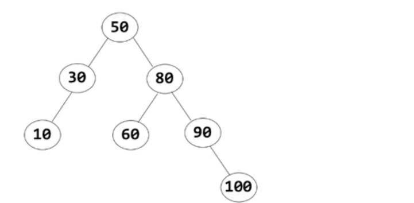
typedef int DataType; typedef struct BiTNode { DataType data; struct BiTNode *left,*right; }BiTNode;
7.1 插入操作
void biTInsert(BiTNode **root,DataType data) { if(*root==NULL) { BiTNode *p=(BiTNode *)malloc(sizeof(BiTNode)); p->data=data; p->left=p->right=NULL; *root=p; } else if((*root)->data<data) biTInsert(&((*root)->right),data); else biTInsert(&((*root)->left),data); }
7.2 删除操作
1 void biTDelete(BiTNode **root,DataType data) 2 { 3 if(*root==NULL) 4 return; 5 else if((*root)->data==data) 6 { 7 BiTNode *p=*root; 8 if((*root)->left==NULL) 9 *root=(*root)->right; 10 else if((*root)->right==NULL) 11 *root=(*root)->left; 12 else 13 { 14 BiTNode *q=p->left; 15 while(q->right) 16 { 17 p=q; 18 q=q->right; 19 (*root)->data=q->data; 20 if(*root==p) 21 p->left=q->left; 22 else 23 p->right=q->left; 24 p=q; 25 } 26 free(p); 27 } 28 else if((*root)->data<data) 29 biTInsert(&((*root)->right),data); 30 else 31 biTInsert(&((*root)->left),data); 32 } 33 }
7.3 遍历操作
BiTNode *biTTraverse(BiTNode *root,void(*visitFunc)(DataType data)) { biTTraverse(root->left); visitFunc(root->data); biTTraverse(root->right); }
7.4 创建操作
BiTNode *biTCreate() { BiTNode *root; int data; do { printf("输入树中一个结点:"); scanf("%d",&data); biTInsert(&root,data); }while(data != -1); return root; }

