数据结构——图

1 图的定义

多对多的数据结构，由顶点的非空集合和顶点之间的边的集合组成；

1.1 图的概念

数据元素

在线性表中称为元素；在树中称为结点、在图中称为顶点

数据元素集合

在线性表中可以没有元素称为空表；在树中可以没有结点称为空树；在图中不能没有顶点，即顶点集合不能为空

数据元素之间的关系

在线性表中称为线性关系；在树中称为层次关系；在图中称为边的关系，边的集合可以为空；

1.2 图的种类

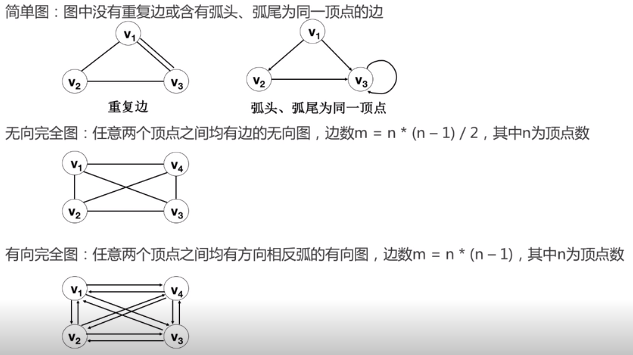
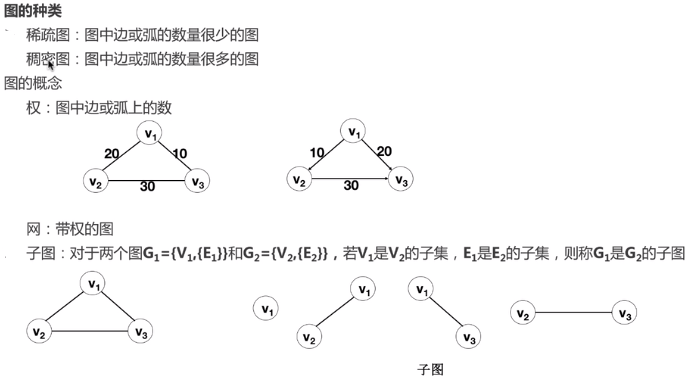
1.3 图的概念

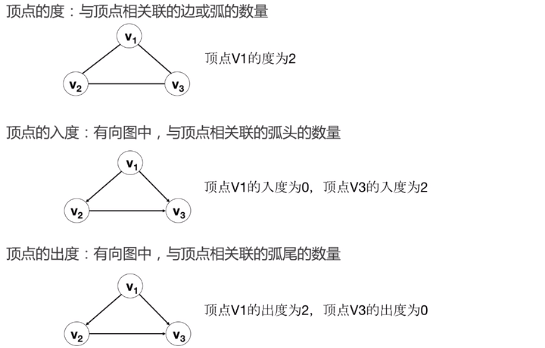
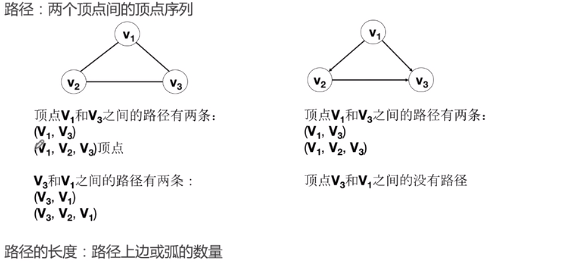
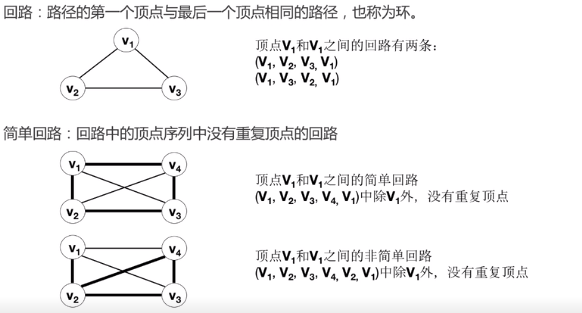
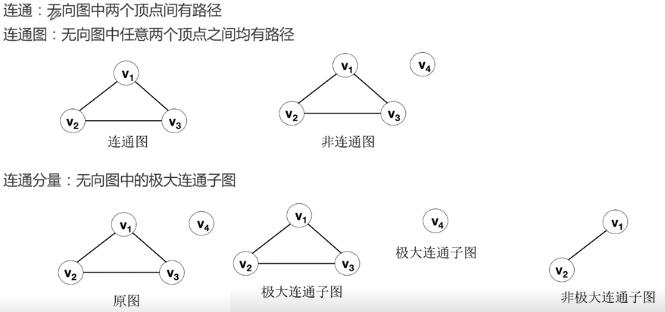
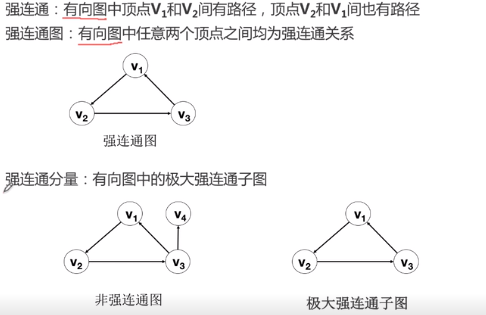
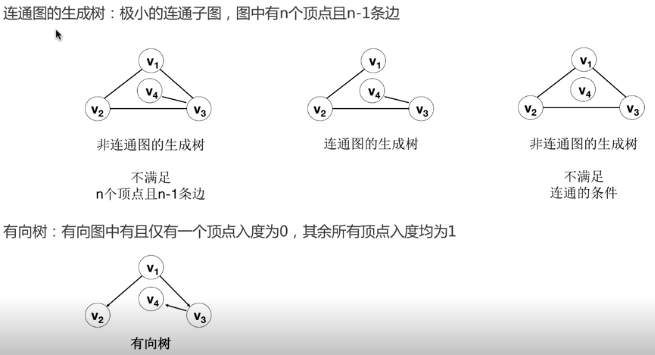
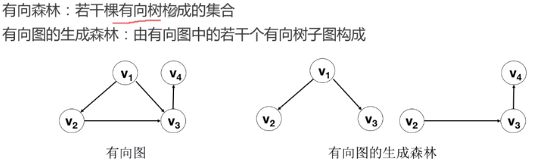
2 图的抽象数据类型

ADT图

data：顶点的非空又穷集合和边的有限集合

operation
  creatGraph(G,V,VR) //按照顶点集合V和边的集合VR构建图G
  destroyGraph(G) //销毁图G
  locateGraph(G,V)//若图G中存在顶点V，则返回V在图中的位置
  getVex(G,V)//返回图G中,顶点V的值
  putVex(G,V,x)//将图G中顶点V赋值为x
  firstAdjVex(G,V)//获取图G中顶点V的一个邻接顶点
  nextAdjVex(G,V,W)//获取图G中顶点V相对于顶点W的下一个邻接顶点
  insertVex(G,V)//在图G中添加一个顶点V
  deleteVex(G,V)//删除图G中的顶点V，及相关的边
  insertArc(G,V,W)//在图G中添加弧<V,W>
  deleteArc(G,V,W)//在图G中删除弧<V,W>
  DFSTraverse(G)//图G的先深搜索
  HFSTraverse(G)//图G的先广搜索
endADT

3 图的存储结构

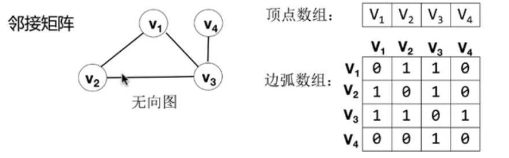
3.1 邻接矩阵

由两个数组表示图；一个是存储顶点的数组，一维数组；一个是存储边或弧的数组，二维数组；

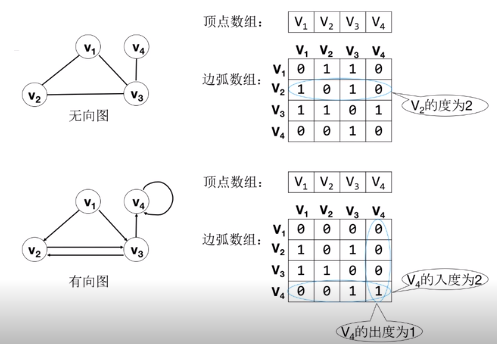
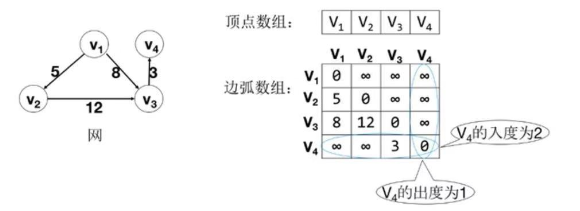
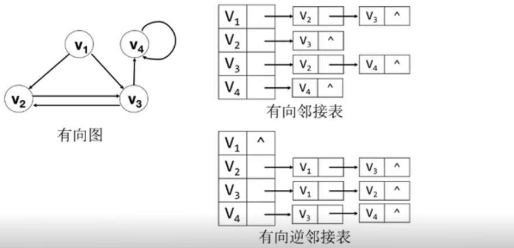
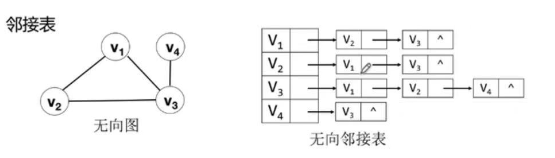
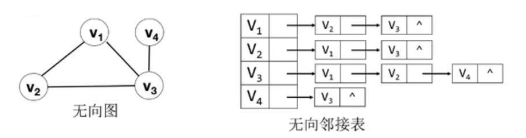
3.2 邻接表

由数组和链表表示图；一个是存储顶点的数组，每个数组元素由顶点、第一条边指针组成；还有一个存储边或弧的链表；

结点结构

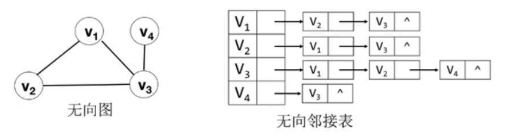
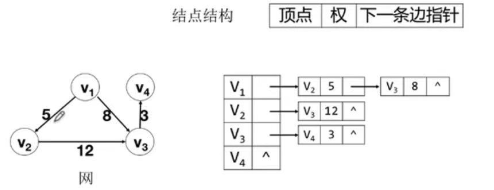
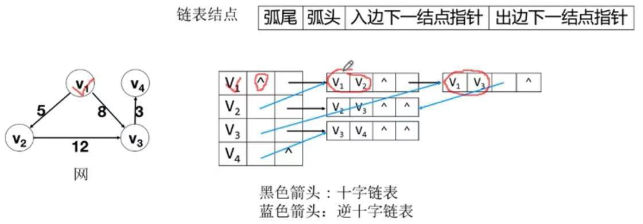
3.3 十字链表

由一维数组和链表表示图；一个是存储顶点的一维数组，每个数组元素由顶点、入边结点指针、出边结点指针组成；还有一个存储边或弧的十字链表；

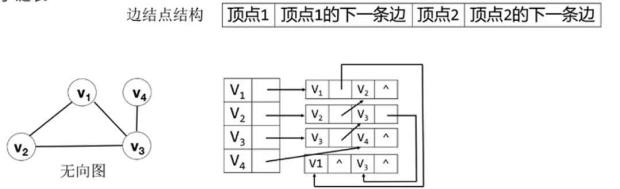
3.4 邻接多重表

由数组和链表表示图；一个存储顶点的数组；还有一个是存储边的十字链表

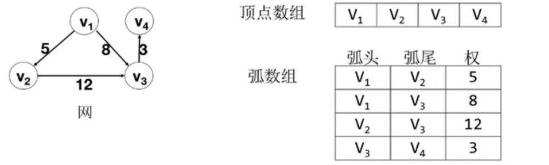
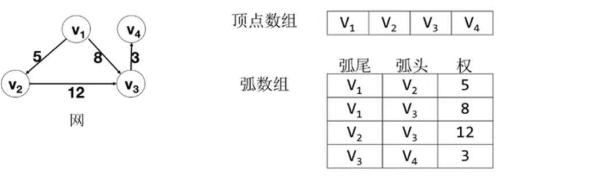
3.5 边集数组

由二个一维数组表示图；一个是存储顶点的数组；另一个是存储边或弧的数组，每个数组元素由弧头、弧尾、权组成；

4 图的遍历

从图中某一顶点出发，使图中其余顶点都被访问到，且仅被访问一次的方法

具体方法是通过定义一个数组visited[n],其中：

n：表示图中顶点的个数

visited[i]的值，(n>i>=0)

值为0表示该顶点未被访问过；

值为1表示该顶点已被访问过；

图的遍历方法

深度优先搜索

广度优先搜索

4.1 深度优先搜索

4.1.1 邻接矩阵

typedef int VType;  //顶点的数据类型
typedef int EType;  //边的数据类型
#define VSIZE 100;  //最大顶点数
typedef struct AdjMGraph  
{
  VType vex[VSIZE];  //顶点数组
  EType arc[VSIZE][VSIZE];  //边弧数组
  int VNum;
  int ENum;
}AdjMGraph;

/*
创建邻接矩阵
*/
void creatAdjMGraph(AdjMGraph *g)
{
  printf("输入顶点个数:");
  scanf("%d",&g->VNum);
  printf("输入顶点间的边数:");
  scanf("%d",&g->ENum);
  for(int i=0;i<g->VNum;i++)
    scanf("%d",&g->vexs[i]);
  for(int i=0;i<g->VNum;i++)
    for(int j=0;j<g->VNum;j++)
      g->arc[i][j]=0;
  for(int k=0;k<g->ENum;k++)
  {
    printf("输入边(vi,vj)的下标i,j");
    int i,j;
    scanf("%d %d",&i,&j);
    g->arc[i][j]=g->arc[j][i]=1;
  }
}

int visited[VSIZE];
void (*visitFunc)(VType t);

void print(VType t)
{
  printf("%d\n",t);
}

void DFS(AdjMGraph g,int i)
{
  visited[i]=1;
  visitFunc(g.vexs[i]);
  for(int j=0;j<g.VNum;j++)
  {
    if(g.arc[i][j]==1 && visited[j]==0)
    {
      DFS(g,j);
    }
  }
}

void DFSTraverse(AdjMGraph g,void (*vf)(VType t))
{
  visitFunc=vf;
  for(int i=0;i<g.VNum;i++)
  {
    visited[i]=0;
  }
  for(int i=0;i<g.VNum;i++)
  {
    if(visited[j]==0)
    {
      DFS(g,j);
    }
  }
}

void main()
{
  AdjMGraph g;  //定义邻接矩阵图
  creatAdjMGraph(&g);  //创建邻接矩阵图
  DFSTraverse(g,print); //遍历邻接矩阵图
}

4.1.2 邻接表

typedef int VType;  //顶点的数据类型
typedef int EType;  //边的数据类型
#define VSIZE 100;  //最大顶点数
typedef struct ENode  //边链表结点
{
  int v; //顶点下标
  struct ENode *next; //下一个顶点的指针
}ENode;

typedef struct VNode //顶点表结点
{
  VType data; //顶点中的数据
  struct VNode *first; //第一个边链表结点的指针
}VNode;

typedef struct AdjMGraph
{
  VType vex[VSIZE];  //顶点数组
  int VNum; //顶点数
  int ENum; //边数
}AdjMGraph;

/*
创建邻接表
*/
void creatAdjMGraph(AdjMGraph *g)
{
  printf("输入顶点个数:");
  scanf("%d",&g->VNum);
  printf("输入顶点间的边数:");
  scanf("%d",&g->ENum);
  for(int i=0;i<g->VNum;i++)
  {
    printf("输入顶点%d的数据:",i);
    scanf("%d",&g->vexs[i].data);
    g->vexs[i].first=NULL;
  }
  for(int k=0;k<g->ENum;k++)
  {
    printf("输入边(vi,vj)的下标i,j");
    int i,j;
    scanf("%d %d",&i,&j);
    ENode *p=(ENode*)malloc(sizeof(ENode));
    p->v=j;
    p->next=g->vexs[i].first;
    g->vexs[i].first=p;
    p=(ENode*)malloc(sizeof(ENode));
    p->v=i;
    p->next=g->vexs[i].first;
    g->vexs[i].first=p;
  }
}

int visited[VSIZE];
void (*visitFunc)(VType t);

void print(VType t)
{
  printf("%d\n",t);
}

void DFS(AdjMGraph g,int i)
{
  visited[i]=1;
  visitFunc(g.vexs[i].data);
  ENode *p=g.vexs[i].first;
  while(p)
  {
    if(visited[p->v]==0)
      DFS(g,p->v);
    p=p->next;
  }
}

void DFSTraverse(AdjMGraph g,void (*vf)(VType t))
{
  visitFunc=vf;
  for(int i=0;i<g.VNum;i++)
  {
    visited[i]=0;
  }
  for(int i=0;i<g.VNum;i++)
  {
    if(visited[j]==0)
    {
      DFS(g,j);
    }
  }
}

void main()
{
  AdjMGraph g;  //定义邻接矩阵图
  creatAdjMGraph(&g);  //创建邻接矩阵图
  DFSTraverse(g,print); //遍历邻接矩阵图
}

4.2 广度优先搜索

4.2.1 邻接矩阵

typedef int VType;  //顶点的数据类型
typedef int EType;  //边的数据类型
#define VSIZE 100;  //最大顶点数
typedef struct AdjMGraph  
{
  VType vex[VSIZE];  //顶点数组
  EType arc[VSIZE][VSIZE];  //边弧数组
  int VNum; //顶点个数
  int ENum;  //边弧的个数
}AdjMGraph;

/*
创建邻接矩阵
*/
void creatAdjMGraph(AdjMGraph *g)
{
  printf("输入顶点个数:");
  scanf("%d",&g->VNum);
  printf("输入顶点间的边数:");
  scanf("%d",&g->ENum);
  for(int i=0;i<g->VNum;i++)
    scanf("%d",&g->vexs[i]);
  for(int i=0;i<g->VNum;i++)
    for(int j=0;j<g->VNum;j++)
      g->arc[i][j]=0;
  for(int k=0;k<g->ENum;k++)
  {
    printf("输入边(vi,vj)的下标i,j");
    int i,j;
    scanf("%d %d",&i,&j);
    g->arc[i][j]=g->arc[j][i]=1;
  }
}

void print(VType t)
{
  printf("%d\n",t);
}

void BFSTraverse(AdjMGraph g,void(*visitFunc)(VType t))
{
  int visited[VSIZE];
  for(int i=0;i<g.VNum;i++)
  {
    visited[i]=0;
  }
  Queue q;
  initQueue(&q);
  for(int i=0;i<g.VNum;i++)
  {
    if(visited[i]==0)
    {
      visited[i]=1;
      visitFunc(g.vexs[i]);
      enQueue(&q,i);
      while(QueueEmpty(q)==0)
      {
        deQueue(&q,&i);
        for(int j=0;j<g.VNum;j++)
        {
          if(g.arc[i][j]==1 && visited[j]==0)
          {
            visited[j]==1;
            visitFunc(g.vexs[j]);
            enQueue(&q,j);
          }
        }
      }
    }
  }
}

4.2.2 邻接表

typedef int VType;  //顶点的数据类型
typedef int EType;  //边的数据类型
#define VSIZE 100;  //最大顶点数
typedef struct ENode  //边链表结点
{
  int v; //顶点下标
  struct ENode *next; //下一个顶点的指针
}ENode;

typedef struct VNode //顶点表结点
{
  VType data; //顶点中的数据
  struct VNode *first; //第一个边链表结点的指针
}VNode;

typedef struct AdjMGraph
{
  VType vex[VSIZE];  //顶点数组
  int VNum; //顶点数
  int ENum; //边数
}AdjMGraph;

/*
创建邻接表
*/
void creatAdjMGraph(AdjMGraph *g)
{
  printf("输入顶点个数:");
  scanf("%d",&g->VNum);
  printf("输入顶点间的边数:");
  scanf("%d",&g->ENum);
  for(int i=0;i<g->VNum;i++)
  {
    printf("输入顶点%d的数据:",i);
    scanf("%d",&g->vexs[i].data);
    g->vexs[i].first=NULL;
  }
  for(int k=0;k<g->ENum;k++)
  {
    printf("输入边(vi,vj)的下标i,j");
    int i,j;
    scanf("%d %d",&i,&j);
    ENode *p=(ENode*)malloc(sizeof(ENode));
    p->v=j;
    p->next=g->vexs[i].first;
    g->vexs[i].first=p;
    p=(ENode*)malloc(sizeof(ENode));
    p->v=i;
    p->next=g->vexs[i].first;
    g->vexs[i].first=p;
  }
}

void print(VType t)
{
  printf("%d\n",t);
}

void DFSTraverse(AdjMGraph g,void(*visitFunc)(VType t))
{
  int visited[VSIZE];
  for(int i=0;i<g.VNum;i++)
  {
    visited[i]=0;
  }
  Queue q;
  initQueue(&q);
  for(int i=0;i<g.VNum;i++)
  {
    if(visited[i]==0)
    {
      visited[i]=1;
      visitFunc(g.vexs[i].data);
      enQueue(&q,i);
      while(QueueEmpty(q)==0)
      {
        deQueue(&q,&i);
        ENode *p=g.vexs[i].first;
        while(p)
        {
          if(visited[p->v]==0)
          {
            visited[p->v]==1;
            visitFunc(g.vexs[p->v].data);
            enQueue(&q,p->v);
          }
          p=p->next;
        }
      }
    }
  }
}

void main()
{
  AdjMGraph g;  //定义邻接矩阵图
  creatAdjMGraph(&g);  //创建邻接矩阵图
  DFSTraverse(g,print); //遍历邻接矩阵图
}

posted @ 2019-04-22 16:15 dongry 阅读(830) 评论(0) 编辑收藏举报

刷新页面返回顶部

dongry

数据结构——图

公告