蒙特卡洛树搜索:
MCTS使用蒙特卡洛模拟来估计每个节点的价值. 其默认策略为贪婪算法, 即每次选择价值最高的节点进行模拟, 在每次模拟得到结果后, 将结果反馈回每个上级节点, 更新节点价值. 通常来讲, 每个访问到的节点都会加入到树中, 实际上为了节省内存每次只加入一个子节点, 可以通过对旧节点剪枝或多次模拟后再加入新节点来进一步节省内存.
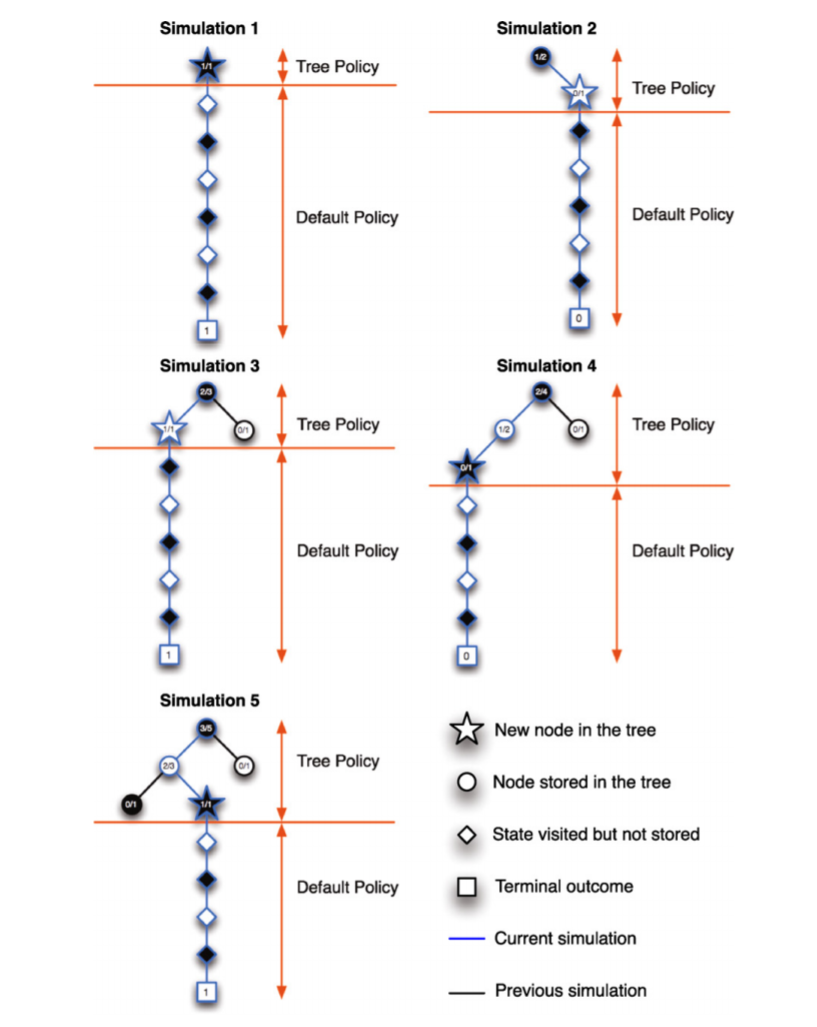
贪婪算法的缺点在于对于一个节点, 如果产生了一次或几次不利的结果后, 搜索树就会避开访问这个节点, 这意味着搜索树的广度会降低, 可能会忽略更好的选择. 这时应该选择UCB1算法(Upper Confidence Bound), 对应节点产生的价值为:
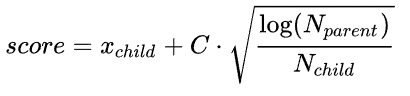
其中C为搜索规模常数, 当C取值越大, 树越偏向广度搜索, 越小就越偏向深度搜索.
AMAF(all moves as first) 算法的核心思想是每一步落子有一个恒定的价值, 不管是什么时候落下的.
当给定状态s, 模拟出期望结果z, 选取a作为后续落子, AMAF value计算为:
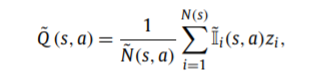
当第i次模拟时, 动作a被执行, 得到状态s时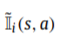
返回1, 否则则返回0
RAVE(rapid action value estimation) RAVE算法融合了蒙特卡洛树搜索和AMAF算法, 它不计算蒙特卡洛价值, 而是计算AMAF价值. 其核心思想是归纳整个子树, 即动作a的价值在状态s下, 或者在子树中其他状态下都一样, 即a的价值是在所有情况下估计得到而不是执行动作时候得到.
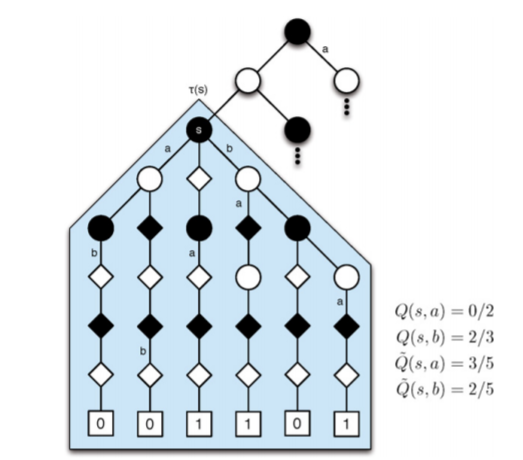
如图, 当使用蒙特卡洛价值估计时, 在s状态下, 如果走a, 会导致两次失败, 价值为0/2, 如果走b, 会有两次成功一次失败, 价值为2/3, 则会选择走b. 当使用AMAF算法价值估计时, 在s状态下, 如果走a, 会有三次成功和两次失败包含动作a, 价值为3/5, 如果走b, 会有两次成功和三次失败包含动作b, 价值为2/5.
RAVE和AMAF算法得到价值会有一定误差但是运行速度较快.
