机器学习实战笔记(1)——k-近邻算法

1. 写在前面

近来感觉机器学习，深度学习神马的是越来越火了，从AlphaGo到Master，所谓的人工智能越来越NB，而我又是一个热爱新潮事物的人，于是也来凑个热闹学习学习。最近在看《Machine Learning IN ACTION》（作者：Peter Harrington）这本书，感觉非常不错。该书不是单纯的进行理论讲解，而是结合了许多小例子深度浅出地进行实战介绍。本博文作为学习笔记，用来记录书中重点内容和稍微地进行知识点的补充，也希望给看到的人带来一些帮助。

目前只看到了第2章，由于是刚开始，因此难度不大。在数学知识上，该章节主要涉及到了初级的线性代数（矩阵的运算）和概率论知识。书中的代码都是用Python 2.7写的，主要用的是NumPy库。本章介绍的是k-Nearest Neighbors（kNN，k-近邻）算法，通过以下3个例子进行说明。

2. kNN简介

对于一个能够采用kNN算法求解的问题的前提通常是：首先需要有一些关于该问题的样本数据集，称为训练集合；然后每条数据都有对应的标签，即我们知道每条数据所属的分类。该类问题的提法通常是：当给定一条未知标签的数据时，我们能够根据样本数据分析出该数据的标签。kNN算法的做法是：将未知标签的数据和样本数据集中的数据相比较，把和未知标签数据最“相近”的一些数据的标签作为未知标签数据的标签。由于“相近”的一些数据的标签可能各自都不相同，因此通常选取k个最为“相近”的标签，统计各标签出现的次数，选取频数最高者。这里“相近”的定义还需要给出。

下面结合3个实战例子进行讲解。

3. 爱情片还是动作片

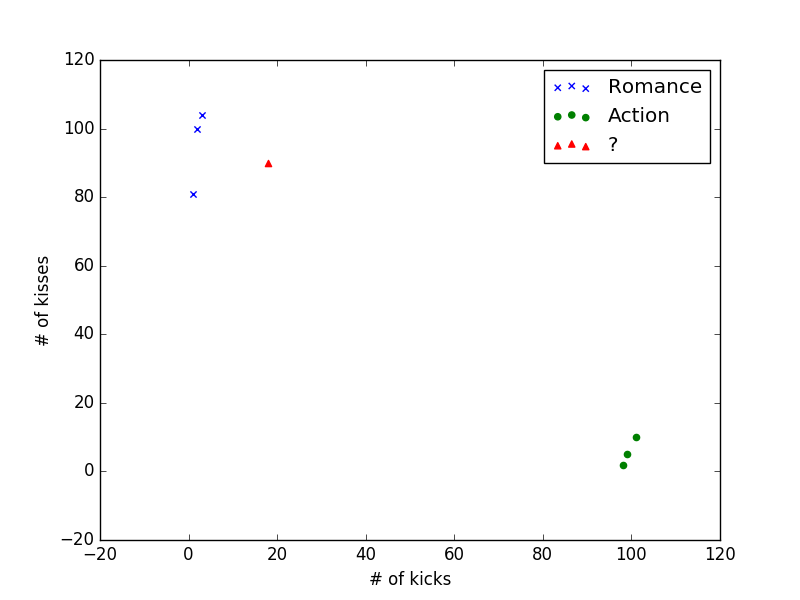
第一个例子是如何判断一部我们还没有看过的电影是爱情片还是动作片。直觉告诉我们，爱情片的亲吻镜头较多，而动作片的打斗镜头较多。为此我们统计了几部爱情片和动作片的亲吻和打斗的镜头数，同时也对待判断的电影（记为电影X）做了统计，我们希望借助于kNN算法判别出电影X是爱情片还是动作片。

如下是统计结果：

电影名称	打斗镜头数	亲吻镜头数	电影类型
California Man	3	104	爱情
He’s Not Really into Dudes	2	100	爱情
Beautiful Woman	1	81	爱情
Kevin Longblade	101	10	动作
Robo Slayer 3000	99	5	动作
Amped II	98	2	动作
X	18	90	?

根据kNN算法，我们需要计算出电影X与其他电影的“距离”，以此作为“相近”的标准。最简单的是采用欧式距离，即我们通常采用的计算平面直角坐标系中两点距离的方法。为此，我们将每部电影的打斗镜头数和亲吻镜头数组成一个平面向量：（打斗镜头数, 亲吻镜头数），对应坐标系中的一点，如下图：

距离计算公式是

\[d = \sqrt{(x - x_0)^2 + (y - y_0)^2} \]

可以求得各部电影与电影X的距离如下表：

电影名称	与电影X的距离
California Man	20.5
He’s Not Really into Dudes	18.7
Beautiful Woman	19.2
Kevin Longblade	115.3
Robo Slayer 3000	117.4
Amped II	118.9

根据kNN算法，假定k=3，即选择3个“最近”的电影，He’s Not Really into Dudes、Beautiful Woman 、California Man，统计其中电影类型出现的频数，爱情片：3；动作片：0。因此我们有理由相信电影X是爱情片。

下面用Python来实现以上的计算过程：

from numpy import *
import operator

def classify(input, train_set, labels, k):
    data_size = train_set.shape[0]
    diff_mat = tile(input, (data_size, 1)) - train_set
    square_diff_mat = diff_mat ** 2
    square_distances = square_diff_mat.sum(axis=1)
    distances = square_distances ** 0.5
    sorted_distances = distances.argsort()
    class_count = {}
    for i in range(k):
        label = labels[sorted_distances[i]]
        class_count[label] = class_count.get(label, 0) + 1
    sorted_class_count = sorted(class_count.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sorted_class_count[0][0]

代码中首先导入了NumPy库，因此需要提前安装（Windows安装可能会出现问题）：

pip install numpy

代码不难，主要是调用了Numpy的一些api。其中array.shape属性是二维元组，正如shape的意思“形状”一样，第一维是行数，第二维是列数。tile函数是将一个数组按行或按列进行复制。sum(axis=1)函数是将数组每行的数据的所有列相加这样得到一个新数组。argsort函数是对数组进行排序，但是得到的排序数组是由数组元素的下标组成的。

下面进行测试：

def test():
  data_set = array([[3, 104], [2, 100], [1, 81], [101, 10], [99, 5], [98, 2]])
  labels = ['Romance', 'Romance', 'Romance', 'Action', 'Action', 'Action']

  print classify([18, 90], data_set, labels, 3)

最终打印Romance，符合我们的预期。

4. 约不约

小明是一个善于交际的人，Ta每年都会结识大量的朋友。Ta将结识的朋友按魅力程度分为了三类: 令人厌恶的人、普通的人、极具魅力的人。根据Ta多年的交际经验，Ta发现一个人的魅力程度可能与那个人的以下3个特征有关：

1. 每年获得的飞行常客的里程数
2. 玩游戏所消耗的时间百分比
3. 每周消费的冰淇淋公升数

于是Ta统计了自己的1000个朋友的上述3个特征的值，按如下格式记录在datingTestSet.txt文件中：

40920	8.326976	0.953952	3
14488	7.153469	1.673904	2
26052	1.441871	0.805124	1
...

数据集中的一行代表一个人的相关数据，前3列是以上所说的3种特征的值，第4列代表魅力程度，值越大表示越具有魅力。

小明希望通过以上的样本数据和一个陌生人的以上3个特征的值来估计这个人的魅力程度，以便让Ta交到更具魅力的朋友。我们可以借助kNN算法来帮助小明结交更具魅力的朋友。

首先我们需要从文件中读入数据：

def read(filename):
    fr = open(filename)
    line = len(fr.readlines())
    data_set = zeros((line, 3))
    labels = []
    fr = open(filename)
    index = 0
    for line in fr.readlines():
        line_list = line.strip().split('\t')
        data_set[index, :] = line_list[0:3]
        labels.append(int(line_list[-1]))
        index += 1;
    return data_set, labels

和之前的例子一样，我们同样用欧式距离来定义“相近”概念，只是本例中多了一个维度。还值得注意的问题是，在上例中，我们直接采用数据的绝对量来计算欧氏距离，那是因为上例中各维度的数据的数量级相同，而在该例中，显然飞行常客里程数远大于另外两个变量的数据，直接计算导致的后果是另外两个变量对距离的影响微乎其微，因此必须统一各变量的数量级。统一的方式是采用如下公式，即转化为相对量：

\[new = \frac{old - min}{max - min} \]

用format函数来完成这件事：

def format(data_set):
    min = data_set.min(0)
    max = data_set.max(0)
    step = max - min
    new_data_set = zeros(shape(data_set))
    line = data_set.shape[0]
    new_data_set = data_set - tile(min, (line, 1))
    new_data_set /= tile(step, (line, 1))
    return new_data_set

接下来需要分类，即计算距离，这步我们直接复用第一个例子的classfy函数。

最后可以进行测试了。一共统计了1000条数据，我们将90%的数据作为样本数据集，剩余10%的数据用来做测试。下面是测试的代码：

def test():
    test_radio = 0.1
    data_set, labels = read('datingTestSet.txt')
    data_set = format(data_set)
    data_count = data_set.shape[0]
    test_count = int(test_radio * data_count)
    train_set = data_set[test_count:, :]
    label_set = labels[test_count:]
    error_count = 0
    for i in range(test_count):
        test_list = data_set[i, :]
        label = classify(test_list, train_set, label_set, 3)
        if not label == labels[i]:
            error_count += 1
    return error_count / float(test_count)

通过以上测试得出错误率是5%，还算不错。因此我们可以使用judge函数来判断一个人的魅力程度，其中x1，x2，x3分别表示飞行常客里程数、玩游戏所耗时间百分比、每周消费冰淇淋升数：

def judge(x1, x2, x3):
    data_set, labels = read('datingTestSet.txt')
    min = data_set.min(0)
    max = data_set.max(0)
    input = (array([x1, x2, x3]) - min) / (max - min)
    return classify(input, format(data_set), labels, 3)

5. 手写识别

第3个例子是采用kNN算法来识别手写数字。手写数字图片已经经过去噪、二值化处理，现储存在文本文件中，比如一张数字0的图片，存储格式如下：

00000000000001100000000000000000
00000000000011111100000000000000
00000000000111111111000000000000
00000000011111111111000000000000
00000001111111111111100000000000
00000000111111100011110000000000
00000001111110000001110000000000
00000001111110000001110000000000
00000011111100000001110000000000
00000011111100000001111000000000
00000011111100000000011100000000
00000011111100000000011100000000
00000011111000000000001110000000
00000011111000000000001110000000
00000001111100000000000111000000
00000001111100000000000111000000
00000001111100000000000111000000
00000011111000000000000111000000
00000011111000000000000111000000
00000000111100000000000011100000
00000000111100000000000111100000
00000000111100000000000111100000
00000000111100000000001111100000
00000000011110000000000111110000
00000000011111000000001111100000
00000000011111000000011111100000
00000000011111000000111111000000
00000000011111100011111111000000
00000000000111111111111110000000
00000000000111111111111100000000
00000000000011111111110000000000
00000000000000111110000000000000

直接看可能看的不是太清楚，我们可以将1替换为空格，并且调整字符的间距，这样可能清楚一些：

我们的样本数据集共有1934条数据，测试数据集共有946条数据，每条数据对应一个文本文件，文本内容格式如上。每个文件的命名方式是：数字_索引.txt。如第一张数字0的图片对应文件的名称是0_1.txt，第3张数字2的图片对应的名称是2_3.txt，因此我们可以通过文件名来知道图片的“标准答案”。

每张图片可以看成一个32x32的矩阵，为了能够满足kNN算法的前提条件，我们需要将每张图片的所有行连接起来，变为1行，这样就变成了1024列；而其对应的标签就是对应的数字。我们用如下read函数去做以上的工作：

def read(train_dir):
    pic_list = os.listdir(train_dir)
    train_set = zeros((len(pic_list), 1024))
    labels = []
    for index, img in enumerate(pic_list):
        train_set[index, :] = read_img(os.path.join(train_dir, img))
        labels.append(int(img[0]))
    return train_set, labels

read函数有调用了read_img函数，它用来读取一张图片，并把该图片转换为一个1x1024的向量。

下面是测试函数：

def test(test_dir):
    train_set, labels = read('trainingDigits')
    pic_list = os.listdir(test_dir)
    error_count = 0
    for index, img in enumerate(pic_list):
        vector = read_img(os.path.join(test_dir, img))
        label = classify(vector, train_set, labels, 3)
        if not label == int(img[0]): error_count += 1
    return error_count / float(len(pic_list))

最后的测试结果为错误率是0.0126849894292，还算不错。

6. 总结

通过以上的3个例子，我们可以感觉到kNN算法具有简单，编程较容易，精确度还比较高的等特点，并且可以想象它对异常值不敏感的；但它的缺点也很明显，比如它的数据应用范围有限，时间以及空间的复杂度都比较高（在第3个例子中明显感觉到）。