语言基础2 矩阵和数组
矩阵和数组是matlab中信息和数据的基本表示形式
可以创建常用的数组和网格 合并现有的数组 操作数组的形状和内容 以及使用索引访问数组元素
用到的函数列表如下
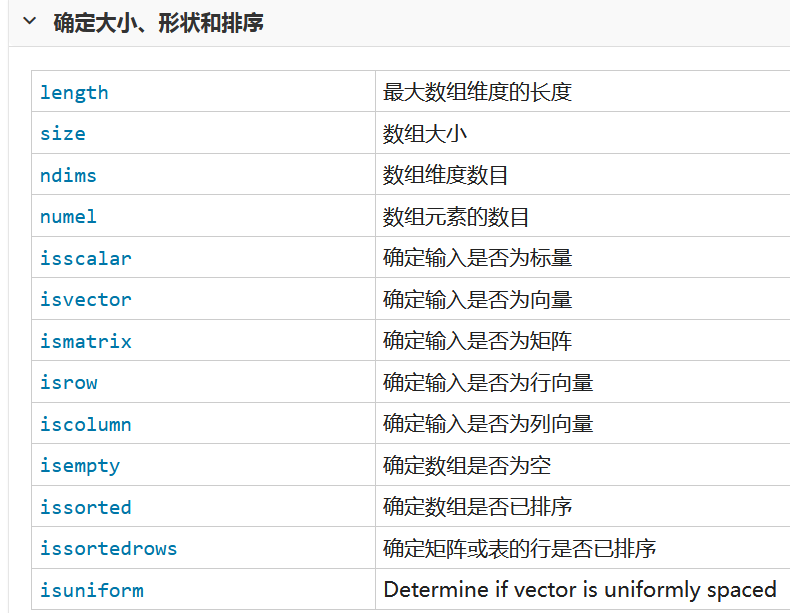
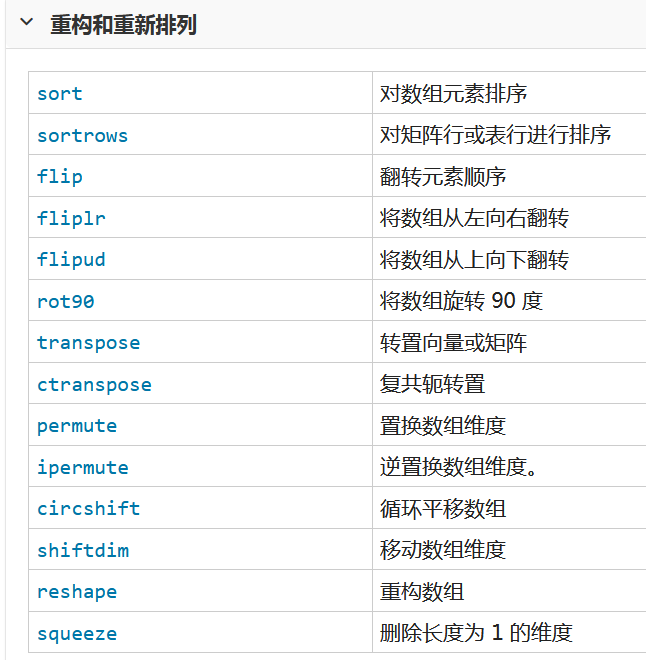
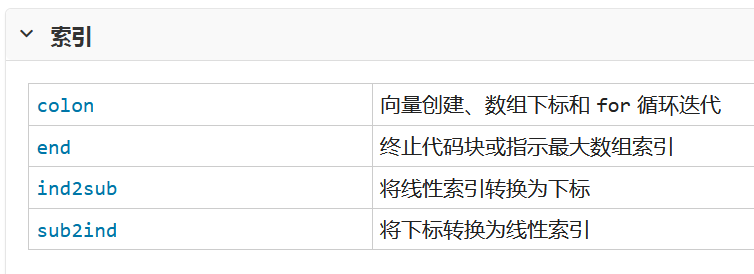
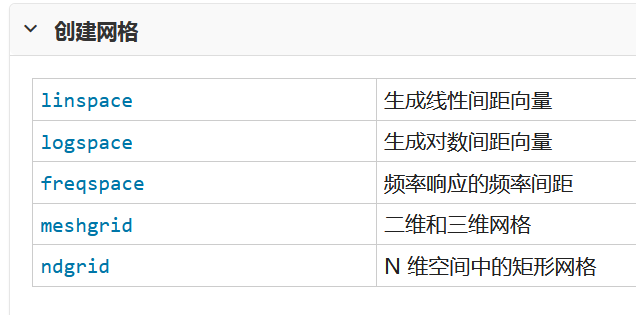
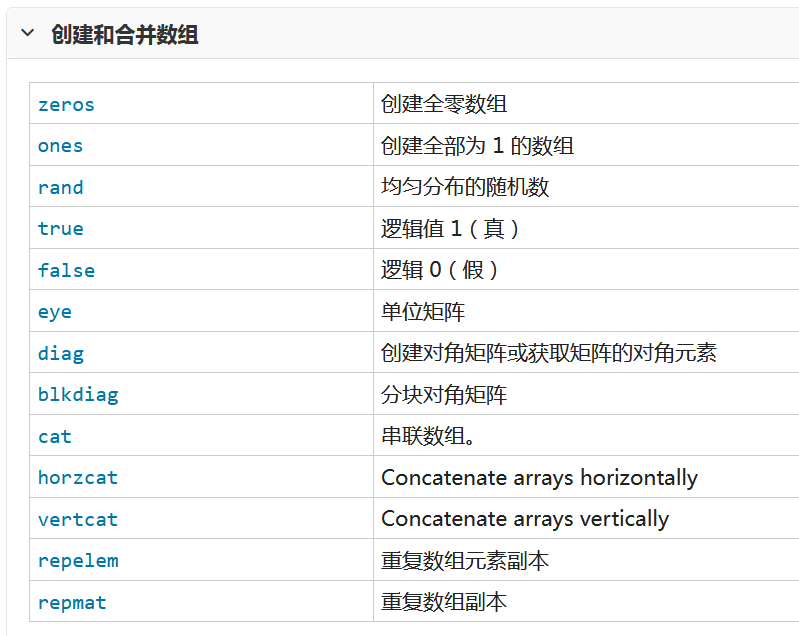
一 创建 串联和扩展矩阵
矩阵时按行和列排列的数据元素的二维数据元素的二维矩形数组。
元素可以是数字、逻辑值、日期时间、字符串、categorical、或其他matlab数据类型
>> A=100; >> whos A Name Size Bytes Class Attributes A 1x1 8 double
构建数据矩阵
>> A=[12 62 93 -8] A = 12 62 93 -8 >> whos A Name Size Bytes Class Attributes A 1x4 32 double
>> A=[12 62;93 -8]
A =
12 62
93 -8
专用矩阵函数
zeros(n1,n2) n1行数 n2列数
ones(n1,n2)
>> zeros(2,3) ans = 0 0 0 0 0 0 >> ones(2,4) ans = 1 1 1 1 1 1 1 1
diag函数将输入元素放在矩阵的对角线上
>> A = [12 62 93 -8]; B = diag(A) B = 12 0 0 0 0 62 0 0 0 0 93 0 0 0 0 -8
串联矩阵
使用方括号来追加现有矩阵 此方法称为串联
>> A=ones(1,4); >> B=zeros(1,4); >> C=[A B] C = 1 1 1 1 0 0 0 0
串联多个矩阵 必须具有兼容的大小,水平串联矩阵时 行数必须相同,垂直串联矩阵,列数必须相同。
串联兼容矩阵的另一种方法时使用串联函数
horzcat vertcat cat
使用horzcat将第二个矩阵水平追加到第一个矩阵
>> D=horzcat(A,B) D = 1 1 1 1 0 0 0 0
使用vertcat将两个矩阵垂直连接
>> E=vertcat(A,B) E = 1 1 1 1 0 0 0 0
生成数值序列
colon 创建由连续且等间距元素组成的矩阵的便捷方式。例如创建一个行向量 其元素是从1到10的整数
>> A=1:10 默认增量为1 A = 1 2 3 4 5 6 7 8 9 10 >> A=-2.5:2.5 A = -2.5000 -1.5000 -0.5000 0.5000 1.5000 2.5000 >> A=0:2:10 指定增量为2 A = 0 2 4 6 8 10 >> A=6:-1:0 增量为负值 则递减 A = 6 5 4 3 2 1 0 >> A=1:0.2:2.1 增量为非整形值 如果增量值不能平均分指定的范围 则会在超出范围之前在可以达到的最后一个值处自动结束序列 此处最后为2 A = 1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
扩展矩阵
通过想一个或多个元素置于现有行和列索引边界之外,可以将他们添加到矩阵中 matlab会自动用0填充矩阵,使其保持为举行
例如创建一个2x3矩阵 然后在(3,4)的位置插入一个元素 使矩阵增加一行一列
>> A=[10 20 30;60 70 80] %A 为2x3 A = 10 20 30 60 70 80 >> A(3,4)=1 此时(1,3)(2,3) 两个位置为0 此时A为3x4 A = 10 20 30 0 60 70 80 0 0 0 0 1
还可以通过现有索引范围之外插入新矩阵来扩展其大小
>> A(4:5,5:6)=[2 3;4 5] 执行完成后 A为5x6 矩阵 未赋值的索引位置填0 A = 10 20 30 0 0 0 60 70 80 0 0 0 0 0 0 1 0 0 0 0 0 0 2 3 0 0 0 0 4 5
上例中 A(4,5)=2 A(4,6)=3 A(5,5)=4 A(5,6)=5
如果重复扩展矩阵的大小 例如在for循环中,最好要为预计创建的最大矩阵预分配空间,matlab必须在每次大小增加时分配内存,所以时间开销较大。
可以预先生成一个大的全0矩阵
zeros(10000,10000) 行和列都是10000的矩阵
A=zeros(10000,10000) 如再大 需要再矩阵所以范围之外指定元素或将另一个预分配的矩阵与A串联来进行扩展
空数组
指至少有一个维度的长度等于零的数组 空数组可用于以编程方式表示“无”的概念
案例:
>> A=[1 2 3 4]; >> ind=find(A<0) ind = 空的 1×0 double 行向量
许多算法都包含可以返回空数组的函数调用 允许将空数组作为函数参数传递 而不是作为特殊情况处理。
需要自定义空数组的处理方式 可以使用isempty 函数来检查它们
TF=isempty(ind)
TF=logical
1 返回真值
数组索引
根据元素在数组中的位置(索引)访问数组元素的方法主要有三种:按位置索引、线性索引和逻辑索引。
按元素的位置进行索引
指定向量中的单个元素 : A(3,2) 行列式的方式 先给行号 再给列号
指定向量中的多个元素:A()
A = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16] a1=A(3,2) %3行2列 索引对应的值 a2=A(2,[1 3]) %A(2,1) A(2,3) a3=A(1:3,2:4) % 访问第一到第三行、第二到第四列中的元素 a4=A(1:3,2:end) %end为最后一列 a5=A(:,3)%:表示所有行或所有列 此处表示所有行的第3列 全部数据 输出: A = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 a1 = 10 a2 = 5 7 a3 = 2 3 4 6 7 8 10 11 12 a4 = 2 3 4 6 7 8 10 11 12 a5 = 3 7 11 15
通过索引来访问matlab中任何数组的元素 而不管其数据类型或维度如何 例如 直接访问datetime数组的列
datetime数组
>> datetime(2018,1:5,1) %详情参考 datetime()函数详情 ans = 1×5 datetime 数组 2018-01-01 2018-02-01 2018-03-01 2018-04-01 2018-05-01 >> datetime(2018,1,1:5) ans = 1×5 datetime 数组 2018-01-01 2018-01-02 2018-01-03 2018-01-04 2018-01-05
使用单个索引进行索引
线性索引 实际上数据实际的存储方式都是按内存列式存储
>> A=[12 36 91;45 29 48;33 25 11] A = 12 36 91 45 29 48 33 25 11 >> Alinear=A(:) %显示全部 Alinear = 12 45 33 36 29 25 91 48 11 >> A(6) 按列序 定值 ans = 25 >> A(3,2) 按二维数组坐标索引定值 ans = 25
>> s=sum(A(:))
s =
330
sub2ind 和 ind2sub 函数可用于在数组的原始索引和线性索引之间进行转换 例如计算A的第3,2个元素的线性索引。
>> linearidx=sub2ind(size(A),3,2) % 将行,列的形式转换为线性索引单列的形式 所以(3,2)对应单列为6 返回值为6 linearidx = 6 >> [row,col]=ind2sub(size(A),6) % 将单列的线性索引形式转换为行,列定位的形式 返回2个输出的变量 row = 3 col = 2
使用逻辑值进行索引
使用true和false 逻辑指示符也可以对数组进行索引 在处理条件语句时尤其便利。
例如 假设想知道A中的元素是否小于另一个矩阵B中的对应元素
当A中的元素小于B中的对应元素时,小于号运算符返回元素为1的逻辑数组。
>> A=[1 2 6;4 3 6] A = 1 2 6 4 3 6 >> B=[0 3 7;3 7 5] B = 0 3 7 3 7 5 >> ind=A<B %判断A和B的各个对应元素 是否满足小于关系 是为1 否为0 ind = 2×3 logical 数组 0 1 1 0 1 0
上例中得到了满足条件的元素的位置;
已经可以使用ind作为索引数组来检查各个值
matlab 将ind中值1的位置与A和B中的对应元素进行匹配,并在列向量中列出它们的值。
>> Avals=A(ind) 列出A中的值 Avals = 2 3 6 >> Bvals=B(ind) 列出B中的值 Bvals = 3 7 7
is函数还返回逻辑数组 指示输入中的哪些元素满足特定条件。
ismissing函数检查string向量中的哪些元素时缺失值。
>> str=["A" "B" missing "D" "E" missing]; >> ind=ismissing(str) 返回一个索引数组 对应值为1的索引位置的字符缺失 原字符数组中包含missing的索引位置为1 其余为0 ind = 1×6 logical 数组 0 0 1 0 0 1
假设要查找非缺失值元素的值 将~运算符和索引向量ind结合使用即可实现此目的
>> strvals=str(~ind) % strvals = 1×4 string 数组 "A" "B" "D" "E"
查找符合条件的数组元素
通过对数组应用条件来过滤数组元素。
检查矩阵中的偶数元素、查找多维数组中所有0值的位置,或者替换数据中的NaN值。
通过组合使用关系运算符和逻辑运算符来执行这些任务。
> < <= == ~= 逻辑运算符 and or not 分别用& | ~表示 从而应用多个条件。
应用单个条件
rng default 创建一个5x5矩阵 元素为位于1和15之间的随机整数 A=randi(15,5) randi(imax,n) 返回5x5矩阵 其中包含从区间[1,imax]的均匀离散分布中得到的伪随机整数
A =
13 2 3 3 10 14 5 15 7 1 2 9 15 14 13 14 15 8 12 15 10 15 13 15 11
>> B=A<9 使用小于号关系运算符 确定A中的哪些元素小于9 将结果存储在B中 B = 5×5 logical 数组 0 1 1 1 0 0 1 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 B为逻辑矩阵 每个值都表示为逻辑值的状态 符合的元素索引位置为1 否则为0 假
>> A(B) B中不会指出这些元素的具体值是多少 但是可以使用B创建A的索引 从而得出满足条件的值 ans = 以列的形式展示出来 2 2 5 3 8 3 7 1
由于B为逻辑矩阵 所以上面的运算称为逻辑索引
有时某些问题需要符合条件的数组元素的位置信息 而非其实际值。
案例可以使用find函数来查找A中小于9的所有元素
>> I=find(A<9) I = 3 6 7 11 14 16 17 22 返回的是一个由线型索引组成的列向量 每个索引描述A中一个小于9的元素的位置 因此实际上A(I)与A(B)返回的结果相同
差别为A(B) 使用逻辑索引 而A(I)使用线性索引
应用多个条件
使用and or not 运算符将任意多个条件应用于一个数组;条件的数量并不局限于一个或两个。
首先,使用逻辑and运算符 由&表示 指定两个条件:元素必须小于9且大于2 将这些条件指定为逻辑索引 以查看符合两个条件的元素。
>> A(A<9 & A>2) ans = 5 3 8 3 7
结果为A中同时符合这两个条件的元素的列表。
务必使用单独的语句指定每个条件,并用逻辑运算符连接起来。
例如:
不能通过A(2<A<9)指定以上条件,因为其计算结果为A(2<A|A<9).
接下来,查找A中小于9且为偶数的元素。
>> A(A<9&~mod(A,2)) ans = 2 2 8 线型排序 列向 显示A中小于9的所有偶数元素的列表 使用逻辑NOT运算符~将矩阵mod(A,2)转换为逻辑矩阵
并在可被2整除的元素位置防止逻辑值1 true
案例2:
查找A中小于9 为偶数且不等于2的元素
>> A(A<9&~mod(A,2)&A~=2) 返回具体的值 ans = 8
>> find(A<9&~mod(A,2)&A~=2) 返回元素所在的位置 索引 线性索引 ans = 14 即A(14)=8
替换符合条件的值
同时更改多个现有数组元素的值会很有用。将逻辑索引与简单的赋值语句一起使用,可替换数组中符合条件的值。
将A中所有大于10的所有值替换为数值10
>> A(A>10)=10 A = 10 2 3 3 10 10 5 10 7 1 2 9 10 10 10 10 10 8 10 10 10 10 10 10 10 >>
>> A(A~=10)=NaN %将A中不等于10的所有值替换为NaN值 A = 10 NaN NaN NaN 10 10 NaN 10 NaN NaN NaN NaN 10 10 10 10 10 NaN 10 10 10 10 10 10 10 >> A(isnan(A))=0; 将A中所有NaN值替换为0 并应用逻辑NOT运算符 ~A >> C=~A
C =
5×5 logical 数组
0 1 1 1 0
0 1 0 1 1
1 1 0 0 0
0 0 1 0 0
0 0 0 0 0
生成矩阵用逻辑值1 替代NaN值 用逻辑值0取代10 逻辑NOT运算~A将数值数组转换为逻辑数组,因此A&C返回逻辑值0 的矩阵 A|C返回逻辑值1的矩阵。



