expectation-maximization algorithm ---- PRML读书笔记
An elegant and powerful method for finding maximum likelihood solutions for models with latent variables is called the expectation-maximization algorithm, or EM algorithm.
If we assume that the data points are drawn independently from the distribution, then the log of the likelihood function is given by
lnp(X|π,μ,Σ)=Σnln{ΣkπkN(xn|μk,Σk)}
EM for Gaussian Mixtures
Given a Gaussian mixture model, the goal is to maximize the likelihood function with respect to the parameters(comprising the means and covariances of the components
and the mixing coefficients).
1.Initialize the means μk, covariances Σk and mixing coefficients πk, and evaluate the initial value of the log likelihood.
2.E step. Evaluate the responsibilities using the current parameter values
3.M step. Re-estimate the parameters using the current responsibilities.
4.Evaluate the log likelihood
lnp(X|π,μ,Σ)=Σnln{ΣkπkN(xn|μk,Σk)}
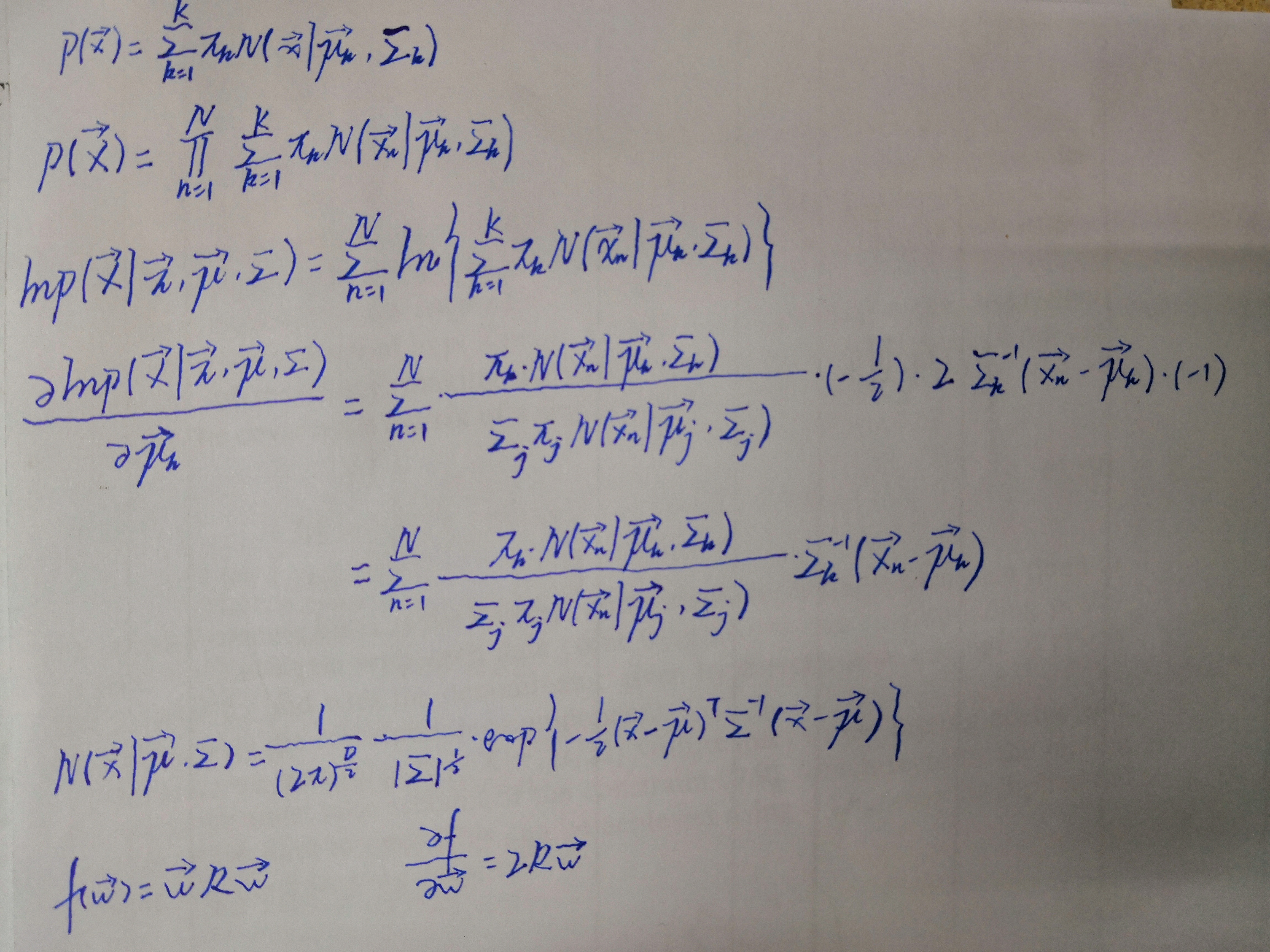




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 25岁的心里话
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现