前缀和

一维前缀和

• 作用：快速查询数组a[l]~a[r]的和，时间复杂度为o(1)。
• 求法：例如数组a[]，用一个数组sum[]来记录它的前n项和，例如sum[n]表示a[1]+a[2]+...+a[n]。

• int sum[1000];
  void init()
  {
      for(int i=1; i<=n; i++)
          sum[i]=sum[i-1]+a[i];
  }
  int query(int l, int r)
  {
      return sum[r]-sum[l-1]; 
  }

加一道前缀和的骚题。。。

这道题居然可以用前缀和来解决，没想到。。。

我们可以枚举自然数段的长度为i

当i为2时，有 12 23 45 67

为i3时有123 234 345 456

为i4时有1234 2345 3456 4567

我们可以发现这些串就可以表示任意一段的区间的和了， 然后奇妙的事发生了， 当要表示长度为i的区间的和时只需要用到第一列的数据和，然后在它的基础上加上k倍的i即可表示

即设前缀和为a[n], 设要表示的数据和为n，如果存在一个区间和能表示这个数， 那么对应存在一个k满足n=sum[i]+k*i;然后上代码。

#include<cstdio>
long long a[2000005];
int main()
{
    int n;
    scanf("%d", &n);
    for(int i=1; i<=2000000; i++)
    {
        a[i]=a[i-1]+i;
    }
    for(int i=2000000; i>=2; i--)
    {
        if(n>=a[i] && (n-a[i])%i==0)
        {
            printf("%d %d\n", 1+(n-a[i])/i, (n-a[i])/i+i);
        }
    }
}

 

二维前缀和

• 作用：快速查询数组a[][]任意二维区间的和
• 求法：用一个数组sum[n][m]表示所有a[n'][m']的和（1<=n'<=n，1<=m'<=m）。
• 下面代码的例图。
• 

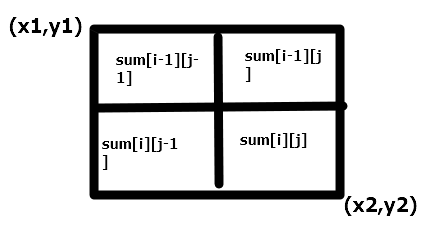
• int sum[1000][1000];
  void init()
  {
      for(int i=1; i<=n; i++)
          for(int j=1; j<=m; j++)
              sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+a[i][j];
  }
  int query(int x1, int y1, int x2, int y2)
  {
      return sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1];
  }

   

 一维差分

• 作用：设数组为a[],对多次a数组上的区间[l,r]实现加减val的操作（将对区间的的操作转化为对两个端点的操作）。
• 做法：

  int a[n];
  int d[n];
  int c[n];
  void init(int l, int r, int val)
  {
      d[l]+=val;d[r+1]-=val;
  }
  for(int    i=1; i<=n; i++)
  {
      c[i]=c[i-1]+d[i];
  }
  for(int i=1; i<=n; i++)
  {
      a[i]+=c[i];
  }

二维差分

• void init(int x1, int y1, int x2, int y2, int val)
  {
      sum[x1][y1] += val;
      sum[x1][y2 + 1] -= val;
      sum[x2 + 1][y1] -= val;
      sum[x2 + 1][y2 + 1] += val;
  }
  
  void get()
  {
      for(int i = 1; i <= n; i++)
          for(int j = 1; j <= n; j++)
              sum[i][j] += sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1];
  }