线段树的收获
关于线段树的理解, 在自己需要时翻看。
什么是线段树?
- 线段树的本质是一棵二叉树,不同于其它二叉树,线段树的每一个节点记录的是一段区间的信息
线段树的功能?
- 更新点,查询区间
-
更新区间,查询点
- 更新区间,查询区间
线段树的优势?
一个长度为N的一维数组(a[1]~a[N])
我们每次对该数组有一些操作:
1、修改数组中某个元素的值
【1,5,4,1,6】---(a[2]=3)---> 【1,3,4,1,6】
2、询问数组中某段区间的最大值
【1,5,4,1,6】---(max(1,4)=?)---> 5
3、询问数组中某段区间的和
【1,5,4,1,6】---(sum(3,5)=?)---> 11
如果只有一次询问?
-
枚举相应区间内的元素,输出答案 O(N)
更多的询问?
-
Q次询问,O(NQ) That's too SLOW!
线段树——在O(log2N)的时间内完成每次操作 O(Qlog2N)
怎么去构造一个线段树?
- e.g. 对于长度为5的数组a[1]~a[5]
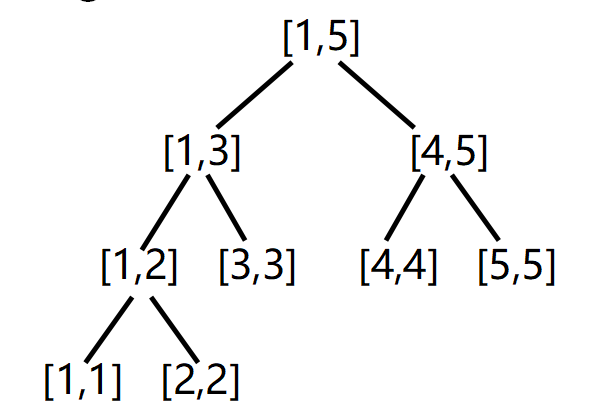
- 对于任一非叶子节点,若该区间为[L,R],则 左儿子为[L,(L+R)/2] 右儿子为[(L+R)/2+1,R]
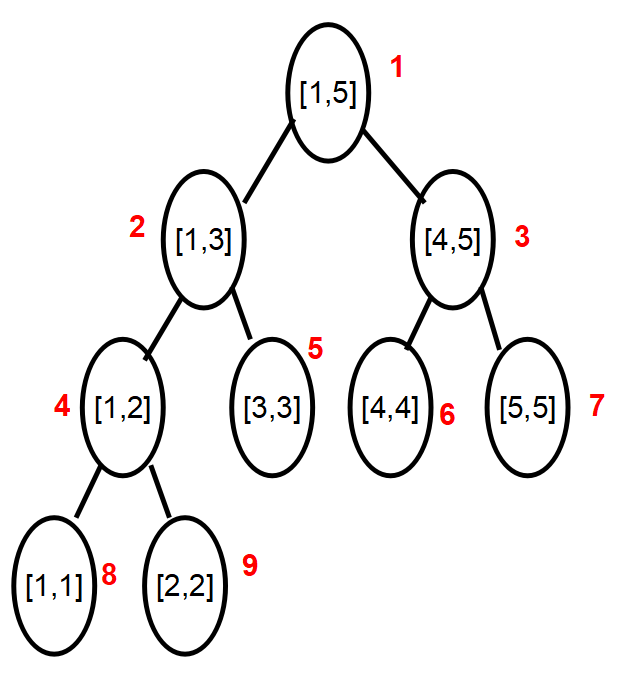
-
我们用一个数组tree记录节点,且根节点的下标为1, 对于任一节点tree[k], 它的左儿子为tree[2*k] 它的右儿子为 tree[2*k+1]
- 这里我习惯用结构体数组, 感觉比较好理解.(也可以只使用一维数组记录最后叶结点的信息, 只不过在函数多加两个参数L,R即可)
-
struct Tree
-
{
-
int left,right; //区间的端点
-
int max,sum; //视题目要求而定
-
};
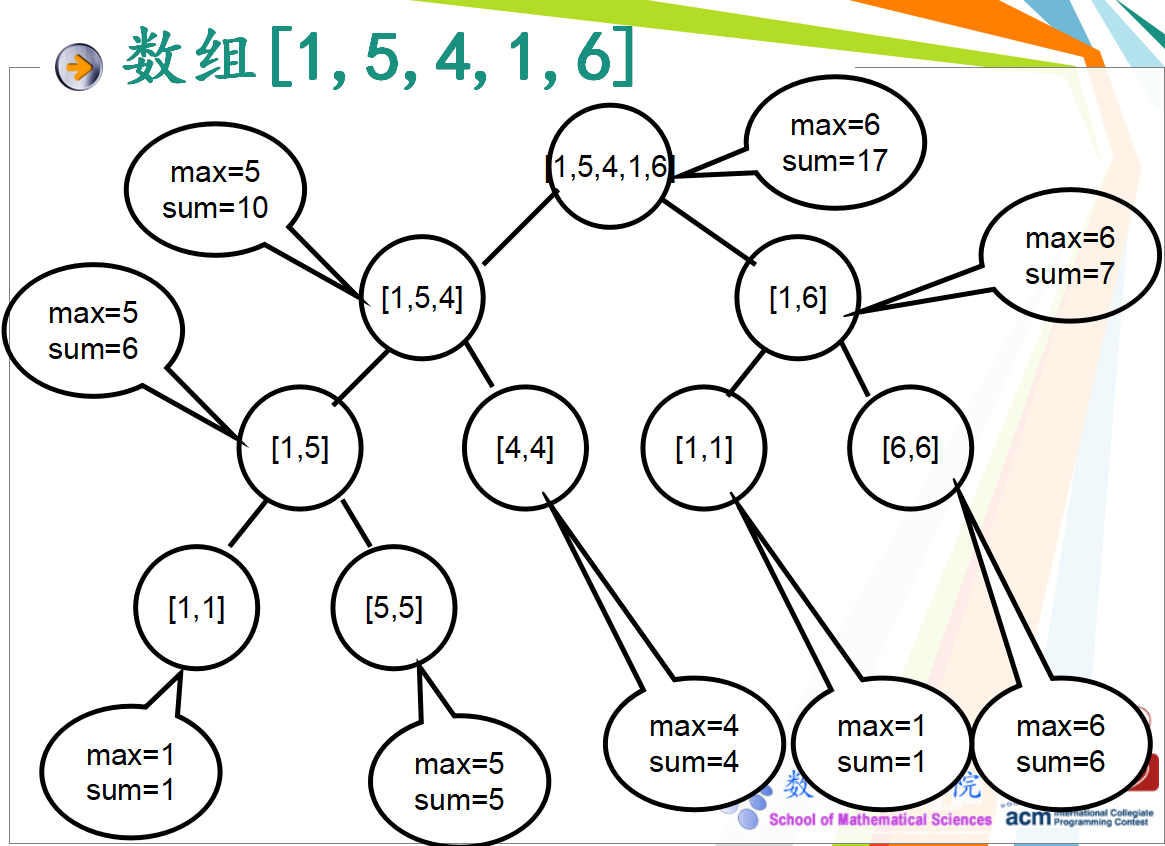
-
如图,就是我们要在线段树中存五个数字所实现的效果。其中, 每个父节点储存了左儿子和右儿子的信息,最后的叶节点储存了数组的信息。
线段树——代码实现(建树)
1 void pushup(int id) 2 { 3 tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum; 4 } 5 void build(int id, int l, int r) 6 { 7 tree[id].left=l;tree[id].right=r; 8 if(l==r) 9 tree[id].maxx=tree[id].sum=a[l]; 10 else 11 { 12 int mid=(l+r)/2; 13 build(id<<1, l, mid); 14 build(id<<1|1, mid+1, r); 15 pushup(id); 16 } 17 }
线段树——代码实现(查询)
1 int query(int id, int l, int r) 2 { 3 if(l<=tree[id].left && tree[id].right<=r) 4 return tree[id].sum; 5 else 6 { 7 int ans; 8 int mid=(tree[id].left+tree[id].right)/2; 9 if(l<=mid) ans+=query(id<<1, l, r); 10 if(r>mid) ans+=query(id<<1|1, l, r); 11 return ans; 12 } 13 }
线段树——代码实现(单点更新)
1 void update(int id, int pos, int val) 2 { 3 if(tree[id].left==tree[id].right) 4 tree[id].sum=tree[id].maxx=val; 5 else 6 { 7 int mid=(tree[id].left+tree[id].right)/2; 8 if(pos<=mid) update(id<<1, pos, val); 9 else update(id<<1|1, pos, val); 10 pushup(id); 11 } 12 }
下面是上面的完全版代码

1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 const int maxn=1e5+5; 5 int a[maxn]; 6 struct note 7 { 8 int left, right, maxx, sum; 9 }tree[maxn*4]; 10 void pushup(int id) 11 { 12 tree[id].sum=tree[id<<1].sum+tree[id<<1|1].sum; 13 } 14 void build(int id, int l, int r) 15 { 16 tree[id].left=l;tree[id].right=r; 17 if(l==r) 18 tree[id].maxx=tree[id].sum=a[l]; 19 else 20 { 21 int mid=(l+r)/2; 22 build(id<<1, l, mid); 23 build(id<<1|1, mid+1, r); 24 pushup(id); 25 } 26 } 27 int query(int id, int l, int r) 28 { 29 if(l<=tree[id].left && tree[id].right<=r) 30 return tree[id].sum; 31 else 32 { 33 int ans; 34 int mid=(tree[id].left+tree[id].right)/2; 35 if(l<=mid) ans+=query(id<<1, l, r); 36 if(r>mid) ans+=query(id<<1|1, l, r); 37 return ans; 38 } 39 } 40 void update(int id, int pos, int val) 41 { 42 if(tree[id].left==tree[id].right) 43 tree[id].sum=tree[id].maxx=val; 44 else 45 { 46 int mid=(tree[id].left+tree[id].right)/2; 47 if(pos<=mid) update(id<<1, pos, val); 48 else update(id<<1|1, pos, val); 49 pushup(id); 50 } 51 } 52 int main() 53 { 54 int n, q, i; 55 cin>>n>>q; 56 for(i=1; i<=n; i++) 57 cin>>a[i]; 58 build(1, 1, n); 59 while(q--) 60 { 61 int op; 62 cin>>op; 63 if(op==1) 64 { 65 int l, r; 66 cin>>l>>r; 67 cout<<query(1, l, r); 68 } 69 else 70 { 71 int pos, val; 72 cin>>pos>>val; 73 update(1, pos, val); 74 } 75 76 } 77 78 }
然后在贴一个线段树区间更新的代码, 也就是在数组中多加了一个懒标记,很好理解.

#include<bits/stdc++.h> using namespace std; const int maxn=1e5+10; int a[maxn]; struct note { int left,right,maxx,lazy; void up(int val) { maxx+=val; lazy+=val; } } tree[maxn*4]; void pushup(int id) { tree[id].maxx=max(tree[id<<1].maxx,tree[id<<1|1].maxx); } void pushdown(int id) { if(tree[id].lazy) { tree[id<<1].up(tree[id].lazy); tree[id<<1|1].up(tree[id].lazy); tree[id].lazy=0; } } void build(int id,int l,int r) { tree[id].left=l; tree[id].right=r; if(l==r) tree[id].maxx=a[l]; else { int mid=(l+r)/2; build(id<<1,l,mid); build(id<<1|1,mid+1,r); pushup(id); } } int query(int id,int l,int r) { if(l<=tree[id].left&&tree[id].right<=r) return tree[id].maxx; pushdown(id); int mid=(tree[id].left+tree[id].right)/2; int ans=-0x3f3f3f3f; if(l<=mid) ans=max(ans,query(id<<1,l,r)); if(r>mid) ans=max(ans,query(id<<1|1,l,r)); return ans; } void update(int id,int l,int r,int val) { if(l<=tree[id].left&&tree[id].right<=r) { tree[id].up(val); return; } pushdown(id); int mid=(tree[id].left+tree[id].right)/2; if(l<=mid) update(id<<1,l,r,val); if(r>mid) update(id<<1|1,l,r,val); pushup(id); } int main() { int n,q; scanf("%d%d",&n,&q); for(int i=1; i<=n; i++) scanf("%d",&a[i]); build(1,1,n); while(q--) { int op; cin>>op; if(op==1) { int l, r; cin>>l>>r; cout<<query(1, l, r)<<endl; } else { int l, r, val; cin>>l>>r>>val; update(1, l, r, val); } } }




