GCN-GAN:对加权动态网络的非线性时间链路预测模型
A Non-linear Temporal Link Prediction Model for Weighted Dynamic Networks GCN-GAN
一、传统方法存在的问题
- 大多数的方法考虑的只是无权网络(但是权重带着重要的信息,链路权重可能包含一些关于网络系统的延迟、流量、信号强度或距离的有用信息);
- 大多数网络的生成过程复杂是非线性的(线性数据表示不能捕捉网络背后不同的潜在变化因素)。
二、我们提出的方法(基于深度学习的加权动态网络时间链路预测模型):
我们结合GCN、LSTM、GAN的长处来加强网络数据的表示学习,在下一次切片中生成高质量的图形快照。
- 首先利用GCN捕获隐藏在每个图快照中的拓扑结构特征;
- 将学习到的网络表示输入到LSTM网络中,以捕获具有多个连续时间片的加权动态网络的演化模式;
- 应用GAN生成具有对抗性训练的高质量和可信的图快照。
在对抗过程中,我们训练生成模型G来根据历史数据顺序预测下一次切片中的加权链路。一个判别模型D也被训练到将生成的链接列表与实际记录区分开来。G和D与极小极大两人游戏联合优化,使模型能够生成高质量的加权链接。
三、问题定义:
G = {G1, G2,…, Gt},Gt = (V, Et, Wt), 时间片tÎ{1,2,t},节点集V,边集Et,权重集Wt ;
无向加权图且节点集不变;
对时间片t,用AtÎR|V|´|V|去描述对应的静态拓扑结构,权重Wt(i, j),其中(At)ij = (At)ji = Wt(i, j)(无边权重为0)
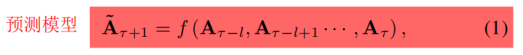
四、方法详细介绍
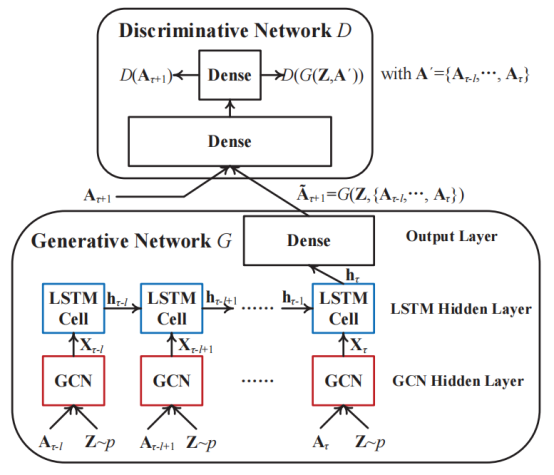
1、总体结构模型
- 首先利用GCN捕获隐藏在每个图快照中的拓扑结构特征;
- 将学习到的网络表示输入到LSTM网络中,以捕获具有多个连续时间片的加权动态网络的演化模式;
- 应用GAN生成具有对抗性训练的高质量和可信的图快照。
2、GCN
我们利用GCN去建模动态网络每个单一快照的本地拓扑结构,GCN是卷积神经网络的一个变体,它可以直接对图进行操作。
我们假设有N个节点,每个节点有M个特征,拓扑结构用矩阵![]() 来表示,节点属性用特征矩阵
来表示,节点属性用特征矩阵![]() 来表示
来表示
具体GCN单元的总体运行可以简要定义如下:
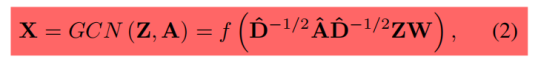
![]() 是近似图的卷积滤波器,
是近似图的卷积滤波器,![]() (IN是一个N维单位矩阵),
(IN是一个N维单位矩阵),![]() ;W代表权重矩阵;f(.)是激活函数;X代表GCN单元给的输出。我们模型中Z被设置为生成网络的噪声输入(根据一定的概率p分布(例如均匀分布))。
;W代表权重矩阵;f(.)是激活函数;X代表GCN单元给的输出。我们模型中Z被设置为生成网络的噪声输入(根据一定的概率p分布(例如均匀分布))。
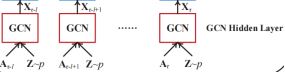
GCN-GAN模型对每个快照输入![]() 都会有
都会有![]() 。基于输入
。基于输入![]() ,GCN层的生成网络会输出一系列数据记作
,GCN层的生成网络会输出一系列数据记作![]() 。
。
3、LSTM
![]() 被输入LSTM层,LSTM它有强大的能力来学习顺序数据的长期依赖关系、时间信息的能力,捕捉加权动态网络的演变模式。
被输入LSTM层,LSTM它有强大的能力来学习顺序数据的长期依赖关系、时间信息的能力,捕捉加权动态网络的演变模式。

最终,我们将最后一个隐藏状态hτ+1作为历史快照的分布式表示,并将其馈送到一个全连接层中,以生成˜Aτ+1的预测结果。
由于学习序列数据的时间信息的能力,可以直接使用LSTM框架(具有多个输入和单个输出)来处理时间链路预测任务。 然而,对加权动态网络的预测仍存在一些局限性。尤其是,为了学习动态网络的时间信息,LSTM通常使用均方误差(MSE)损失函数进行训练。然而,均方误差MSE损失不能反映实际网络系统中链路权值的稀疏性和宽值范围,这在第五节中对进行了实证证明。
4、GAN
为了处理动态网络边权重的稀疏性和宽值范围问题,我们用GAN框架去加强LSTM的生成能力。GAN由一个生成模型G和一个区分模型D构成。首先,D试着区分训练集中的真实数据和G生成的数据;另一方面,G尝试愚弄D并生成高质量的样本(数据)。形式上,这个过程可以描述维如下:
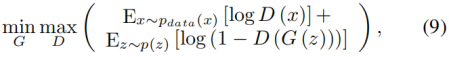
其中x是训练集的输入数据,z表示通过一定概率分布p(Z)产生的噪声(例如均匀分布)。
与上述标准的GAN框架一样,我们的模型还优化了两个神经网络(即生成网络G和判别网络D)。在模型中,D试图将训练数据中的真实图形快照与G生成的快照区分开来,而G最大限度地提高了D犯错误的概率。希望这种对抗性过程最终可以调整G以生成可信和高质量的加权链接。下面我们进一步详细说明这两个神经网络。
(网上对GAN的介绍:在训练过程中,D会接收真数据和G产生的假数据,它的任务是判断图片是属于真数据的还是假数据的。对于最后输出的结果,可以同时对两方的参数进行调优。如果D判断正确,那就需要调整G的参数从而使得生成的假数据更为逼真;如果D判断错误,则需调节D的参数,避免下次类似判断出错。训练会一直持续到两者进入到一个均衡和谐的状态。)
4.1、判别网络
我们通过一个具有一个隐藏层和一个输出层的全连通前馈神经网络来实现了判别模型D。在训练过程中,D也可以将G的输出˜Aτ+1或地面真值Aτ+1作为输入。因为全连接神经网络的每个输入数据通常被表示为一个向量(不是矩阵),因此当将矩阵输入D时,我们将矩阵输入(即˜Aτ+1或Aτ+1)重塑为相应的行长向量。此外,我们使用Wasserstein GAN (WGAN)框架去训练模型,我们把输出层设置为一个线性层,它可以不经过一个非线性激活函数直接生成输出。简单地说,鉴别网络D的细节可以表述如下:
![]()
其中![]() ,a’是其对应的重塑行长向量;分别是隐藏层和输出层的参数;s(.)代表隐藏层的激活函数。
,a’是其对应的重塑行长向量;分别是隐藏层和输出层的参数;s(.)代表隐藏层的激活函数。
因为所给网络快照也许有一个大范围的值(例如[0,2000]),当选择At+1作为D的输入时,我们把At+1的值规范化到[0,1]。G给出的原始预测结果˜Aτ+1被定义在[0,1]的范围内,因此可以直接用作D的输入。
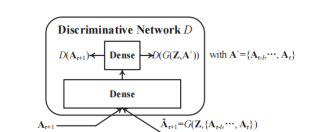
4.2、生成网络
G由一个GCN层和LSTM层和一个全连接输出层构成。GCN层采用图快照序列和噪声Z作为输入,输出用![]() 表示,随后会被喂进LSTM层。需要注意的是每个邻接矩阵输入At在被输入进GCN层时都应该被归一化到[0,1]。另外,我们采用sigmoid作为所有GCN单元的激活函数并且让噪声输入服从[0, 1]的均匀分布。
表示,随后会被喂进LSTM层。需要注意的是每个邻接矩阵输入At在被输入进GCN层时都应该被归一化到[0,1]。另外,我们采用sigmoid作为所有GCN单元的激活函数并且让噪声输入服从[0, 1]的均匀分布。
LSTM层用由GCN给的表示序列![]() 作为输入,输出隐层状态
作为输入,输出隐层状态 。注意每个矩阵输入Xt在被喂进LSTM时都应该被重塑为一个行长向量。最后,最后一个状态ht被喂进输出层去生成下个时间片图快照(它也是对应的行长向量形式)。特别地,生成结果的元素都在[0,1]的范围内。通过进行归一化的反过程,可以得到具有正确的动态网络的值范围的最终预测快照。
。注意每个矩阵输入Xt在被喂进LSTM时都应该被重塑为一个行长向量。最后,最后一个状态ht被喂进输出层去生成下个时间片图快照(它也是对应的行长向量形式)。特别地,生成结果的元素都在[0,1]的范围内。通过进行归一化的反过程,可以得到具有正确的动态网络的值范围的最终预测快照。
生成网络G可以简化为下面的形式
![]()

4.3、模型优化
因为动态网络总是随时间变化,因此GCN-GAN模型应该不断的更新它的参数去适应网络的进化。另外,人们通常认为接近下一次切片(τ+1)的网络快照可以被认为具有与真实值更相似的特性,而不是那些远离它的。基于这样一个合理的假设,我们用下面的优化策略。当涉及到一个新的时间切片τ时,模型首先利用先前的网络图序列![]() 作为输入,当前快照Aτ作为真实值。为当前时间片t训练完模型后,我们指导这个预测过程去用序列作为输入生成下一个图快照
作为输入,当前快照Aτ作为真实值。为当前时间片t训练完模型后,我们指导这个预测过程去用序列作为输入生成下一个图快照![]() 。训练细节和预测过程下面详细阐述。
。训练细节和预测过程下面详细阐述。
对时间链路预测任务来说,直接用标准的对抗训练过程是不合适的,因为G也许会生成一个合理的网络快照去成功的糊弄D,但是它和下一个图快照并不是一致的。事实上,我们希望预测结果应该尽可能靠近真实值At+1。为了去处理这个问题,我们介绍了另一个具有以下损失函数的G的预训练过程:
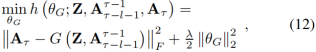
ΘG代表G的参数,l控制L2正则化的系数。上式中,G尝试通过和Z去重新构造当前快照At。这个过程可以帮助G去捕获动态网络最新的时间信息,它被认为是与Aτ+1的真实快照最相似的特性。
在预训练过程之后,G有了生成预测结果的初始能力。这个对抗训练过程可以进一步的发展去加强G的生成能力去处理加权动态网络的稀疏性和宽值范围问题。特别地,我们用Wasserstein GAN (WGAN)框架,它已经被证明比标准的GAN有一个更值得信赖的性能。
【 Wasserstein GAN (WGAN)框架改进后相比原始GAN的算法实现流程却只改了四点:
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行

】
在这个过程中,我们通过固定的(fixed)G的参数通过下面的损失函数用梯度下降法去更新D的参数(记作θD):
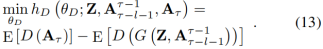
在更新完D的参数后,他们的值应该进一步被剪到预定义的范围[c,-c]。然后我们通过固定的D的参数通过下面的损失函数更新G的参数(记作θG):
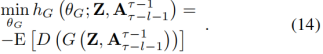
在这个实验中,我们采用RMSProp算法去更新参数θG和θD,直到收敛。
完成训练过程后,G利用![]() 和Z可以生成预测结果
和Z可以生成预测结果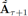 。注意初始的预测结果
。注意初始的预测结果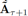 在[0,1]范围内,另一个反归一化过程需要把它的值恢复到网络边权重的真实范围。此外,一些技巧可以用来进一步细化预测结果,其表述如下:
在[0,1]范围内,另一个反归一化过程需要把它的值恢复到网络边权重的真实范围。此外,一些技巧可以用来进一步细化预测结果,其表述如下:

首先我们用(15)去使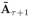 对称,因为我们只考虑无向网络的情况。然后,通过(16)我们设置
对称,因为我们只考虑无向网络的情况。然后,通过(16)我们设置![]() 对角元素的值为0去消除自身链接边的影响。最后,值小于小阈值ε的元素可以设置为0,以反映边缘权重的稀疏性。
对角元素的值为0去消除自身链接边的影响。最后,值小于小阈值ε的元素可以设置为0,以反映边缘权重的稀疏性。
我们在表I中总结了GCN-GAN模型的总体训练和预测过程(当网络系统出现新的时间切片τ时)

五、实验评估
A、数据集
我们对不同网络系统的三个真实数据集和一个仿真数据集进行了实验。
N、T和Max表示一个数据集经过必要的预处理后的节点数、时间切片数和最大边缘权重值。
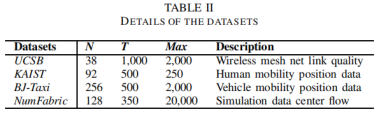
对于UCSB 和 NumFabric,网络系统中的主机可以被描述为动态网络中的节点。此外,在特定时间段中的链路质量或流可以直接表示为在特定快照中对应的主机对之间的链路权重。
对于KAIST 和BJ-Taxi, 我们将每个用户(人或车辆)作为抽象动态网络中的一个节点,并计算了所有时间切片的每一对节点之间的距离。特别地,我们为一个特定的时间切片t构造了一个距离矩阵Dt,用(Dt)ij的=(Dt)ji表示节点i和j之间的距离。在人类移动和车辆移动的实际网络系统中,与相对较大距离的用户相比,一对彼此接近的用户应该得到更多的兴趣或关注。
![]() 特别是,δ是某一网络的最大边权。
特别是,δ是某一网络的最大边权。
此外,我们还对上述四个网络的链路权重的稀疏性和分布进行了统计分析。
连接权重的稀疏性:大多数图的快照都是相对稀疏的,这意味着在一定的时间片的邻接矩阵中有一个不可忽略的零部分。例如,UCSB、KASIT、BJ-Taxi和NumFabric的所有邻接矩阵中零元素的平均部分分别为0.52、0.92、0.94和0.50。(the average por tions of zero elements in all the adjacency matrices)
对于加权时间链路预测任务,(At)ij=0意味着节点i和j之间没有边缘。 另一方面,(At)ij具有较小的值,这意味着这对节点之间仍然有一个边缘,但权重很小。这两种情况完全不同,但对大多数传统的时间链路预测方法来说,区分它们(小边权值和零值)仍然是一个具有挑战性的问题。
事实上,对于大多数网络系统来说,预测模型不能区分小边权值和零值的错误是相对严重的。它可能会错误地引导系统(i)预分配不存在链路的关键资源或(ii)不为存在链路分配资源,导致系统开销的浪费比现有链路权重的正常预测误差更多。
边权值分布:为了确保模型的学习能力,大多数链路预测方法将输入的链路权重归一化到一定的小范围(例如。 [0,1])。然而,当恢复预测快照的值时,非常轻微的误差(在0到1之间)仍然可能导致最终结果中的大误差与均方误差评估度量。

如图所示。 在网络中,很大比例的边缘具有较小的权重。 然而,用于训练和评估时间链路预测模型的常规均方误差(MSE)度量只对具有较大权重的边缘敏感。它不能反映大多数具有小权重的边缘的动态变化,使得加权网络的时间链路预测成为一个具有挑战性的问题。
B、评估指标
为了定量评价我们的时间链路预测模型,我们遵循以前的工作[6],[12]使用均方误差(MSE)分数进行比较,其定义为:
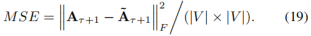
此外,为了进一步评估我们的模型处理上述稀疏性和宽值范围问题的能力,我们引入了两个额外的度量(the edge-wise KL-divergence and the mismatch rate)。
a) The Edge-wise KL-Divergence:
对于一些动态网络,快照的边缘权重可能具有很宽的值范围(例如,[0,2,000]),其中大多数边缘具有相对较小的权重。然而,MSE评分可能只对大的边缘权重敏感,并且难以区分对小权重很重要的大小差异。例如,2和1之间的大小差异应该远远大于2000和1990之间的差异,即使后者的情况会导致更大的MSE误差。为了缓解上述问题,我们引入了edge-wise KL-divergence,以进一步考虑链路权重的大小差异。
首先,我们推导出两个辅助矩阵P和Q来分别表示地真值图快照Aτ+1的标准化值和预测结果的˜Aτ+1的标准化值。我们制定的P和Q标准如下:

然后,将the edge-wise KL-divergence定义为:

其中如果Pij>0并且Qij>0,![]() ,否则。请注意,当Pij=0或Qij=0时,我们只需将它们的KL-散度设置为0,因为零值可能导致NaN或Inf异常,我们在下面的失配率定义中考虑了这种特殊情况。
,否则。请注意,当Pij=0或Qij=0时,我们只需将它们的KL-散度设置为0,因为零值可能导致NaN或Inf异常,我们在下面的失配率定义中考虑了这种特殊情况。
b) The Mismatch Rate:
根据我们对数据集的观察,加权动态网络中边缘权重的稀疏性问题也很重要,需要特别讨论。 我们考虑以下两种情况:

特别是,这两种情况意味着预测结果不正当地确定了边缘(i,j)的存在,这应该被认为是加权动态网络的时间链路预测的严重错误。因此,我们使用the mismatch rate,它表示在某个图快照中这些不匹配边的比例,作为一个额外的评估度量。
C、性能评价
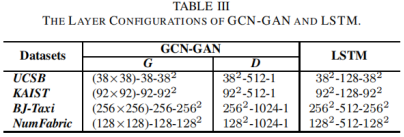
具有mi-mh-mo格式的四个数据集的层配置见表三,其中mi是每个时间步长中输入的大小,mh表示LSTM的隐藏大小,mo是输出的大小。特别是,我们使用N×N表示矩阵输入(N×N的大小),并使用N2表示(行)长向量的大小,可以重塑为N×N矩阵。
这四个数据集的参数设置情况见表四

MSE、边缘KL散度和不匹配率的评价结果分别见表V、表VI和表七,其中最佳性能值为粗体,第二大为下划线。
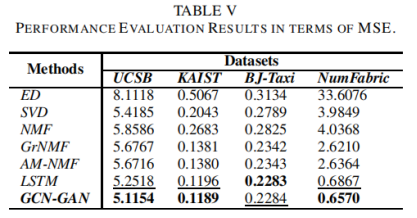

D、个案研究
我们使用从UCSB的预测结果中选择的示例性案例来演示我们的模型生成高质量加权链路的能力。通常,在邻接矩阵中,零元素和那些具有小值的元素具有完全不同的物理意义,因此,我们特别将矩阵中的所有零值设置为−200,以强调这种差异。
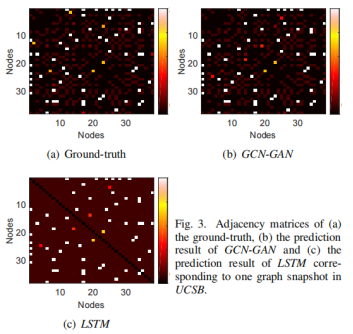
结果见图。 其中子图(A)显示地面真相,子图(B)和(C)分别显示GCN-GAN和LSTM的预测结果。 在热图中,黑色表示邻接矩阵的零值(注意,我们将所有零元素的值设为-200)。 此外,颜色深度表示边缘的权重,其中接近暗红色的颜色表示相对较小的边缘权重,而接近白色的颜色表示较大的值。
如图3所示,GCN-GAN和LSTM都能很好地适应较大的边缘重量(颜色接近白色。然而,LSTM未能区分零值(颜色为黑色)和小边缘权重(颜色接近暗红色)。另一方面,我们的GCN-GAN模型可以有效地应对这种具有挑战性的问题,反映了网络快照边缘权值的稀疏性。
六、结论
我们的模型可以有效地处理加权动态网络的具有挑战性的预测任务,因为它结合了深度神经网络(即GCN和LSTM)在学习网络的综合分布式表示方面的优势,以及GAN在生成高质量的加权链路方面的优势。
更重要的是,如何处理使用不固定节点集的具有挑战性的时间链路预测问题也是我们的下一个研究重点。


