无向网络节点重要性指标
学自书籍:《网络科学导论》高等教育出版社
1、引言:
寻找网络中的关键节点是网络科学的重要研究内容之一。
这一部分就是介绍 无向网络中节点重要性排序的几个常用指标,包括度值、介数、接近数、k-壳值和特征向量。 有向网络中 节点重要性排序的两个经典算法---HITS算法和PageRank算法都是来自WWW上的网页排序。
链路预测的基本想法就是:两个节点越是相似,那么它们之间就越有可能存在连边,这里也介绍多种基于节点相似性的预测方法。
2、无向网络节点重要性指标
2.1 度中心性
例如,一套房子的价值首先要看这套房子所在的地段。同样的在复杂网络中主要就是取决于 位置。也就是说一个节点的价值首先取决于这个节点在网络中所处的位置,位置越中心的节点其价值也越大。
度中心性就是一个节点的度越大就意味着这个节点越重要。 (一个包含N个节点的网络,所以节点最大可能的度值为N-1,度为 ki 的节点的归一化的度中心性值定义为:)
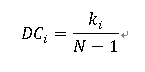 2.2 介数中心性
2.2 介数中心性
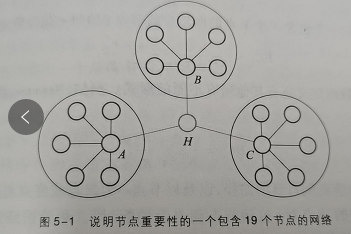
如下图,从度中心性来看,节点A、B、C都比节点H重要。现在假设有信息或者物质在节点之间沿着连边流动,对应与网络中的信息传播、互联网中的数据包发送等。如果两个节点之间存在多条最短路径,那么随机选择一条最短路径,经过相当长一段时间后,每对节点间都传送了许多包,现在问:哪个节点最繁忙,也就是经过哪个节点的包数量最多?
这种以经过某个节点的最短路径的数目刻画节点重要性的指标就称为介数中心性,简称介数(BC)
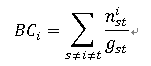
gst为节点s到节点t的最短路径的数目,nsti 为节点s到节点t的 gst条最短路径中经过节点i的最短路径的数目。
Newman给出的归一化介数:
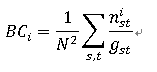
2.3 接近中心性
对于网络中的每一个节点i,可以计算该节点到网络中所有节点的距离的平均值,记为di ,即有:
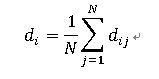
其中di 是节点i到节点j的距离。这样,就可以得到网络的评价路径长度的另一种计算公式:
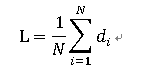
di 在一定程度上反映了节点 i 在网络中的相对重要性:di 的值越小意味着节点 i 更接近其他节点。我们把di 的倒数定义为节点i的接近中心性,简称接近数,用记号CCi 来表示:
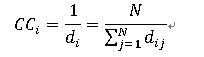
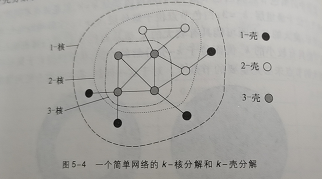
2.4 k-壳与k-核
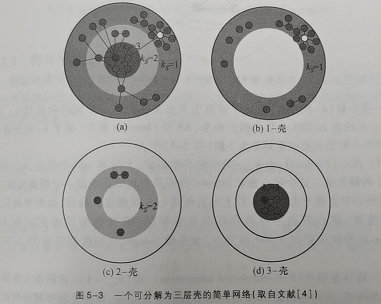
粗粒化的节点重要性分类方法, 即k-壳分解方法
1-壳:假设网络中不存在度为0的鼓励节点。如果我们把度为1的节点以及这些节点相连的边去掉,这时网络中优惠出现一些新的度为1的节点,我们继续把这些节点及其连边去掉,重复这个操作,直至网络中不再有度为1的节点为止。这个操作相当于剥去一层壳,我们就把所有这些被去除的节点以及它们之间的连边称为网络的1-壳(1-shell)。有时,网络中度为0的鼓励节点也称为0-壳。
2-壳:在1-壳的基础上继续剥出度为2的那层壳。 以此类推。
下图显示了一个可分解为三层壳的简单网络。
2.5 特征向量中心性
基本想法:一个节点的重要性既取决于其邻居节点的数量(即该节点的度),也取决于其邻居节点的重要性。记xi 为节点i的重要性度量值,则:
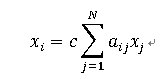
其中c为一比例常数, A=(aij )仍然是网络的邻接矩阵。记x=[x1,x2....xn]T ,则上式可以写成如下矩阵形式:
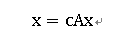
上式意味着x是矩阵A与特征值c-1对应的特征向量,故此称为特征向量中心性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号