k-means
前面理论部分转自
https://www.jianshu.com/p/fc91fed8c77b说到聚类,应先理解聚类和分类的区别,很多业务人员在日常分析时候不是很严谨,混为一谈,其实二者有本质的区别。
分类:分类其实是从特定的数据中挖掘模式,作出判断的过程。比如Gmail邮箱里有垃圾邮件分类器,一开始的时候可能什么都不过滤,在日常使用过程中,我人工对于每一封邮件点选“垃圾”或“不是垃圾”,过一段时间,Gmail就体现出一定的智能,能够自动过滤掉一些垃圾邮件了。这是因为在点选的过程中,其实是给每一条邮件打了一个“标签”,这个标签只有两个值,要么是“垃圾”,要么“不是垃圾”,Gmail就会不断研究哪些特点的邮件是垃圾,哪些特点的不是垃圾,形成一些判别的模式,这样当一封信的邮件到来,就可以自动把邮件分到“垃圾”和“不是垃圾”这两个我们人工设定的分类的其中一个。
聚类:聚类的目的也是把数据分类,但是事先我是不知道如何去分的,完全是算法自己来判断各条数据之间的相似性,相似的就放在一起。在聚类的结论出来之前,我完全不知道每一类有什么特点,一定要根据聚类的结果通过人的经验来分析,看看聚成的这一类大概有什么特点。
聚类和分类最大的不同在于:分类的目标是事先已知的,而聚类则不一样,聚类事先不知道目标变量是什么,类别没有像分类那样被预先定义出来。
K-Means
聚类算法有很多种(几十种),K-Means是聚类算法中的最常用的一种,算法最大的特点是简单,好理解,运算速度快,但是只能应用于连续型的数据,并且一定要在聚类前需要手工指定要分成几类。
下面,我们描述一下K-means算法的过程,为了尽量不用数学符号,所以描述的不是很严谨,大概就是这个意思,“物以类聚、人以群分”:
- 首先输入k的值,即我们希望将数据集经过聚类得到k个分组。
- 从数据集中随机选择k个数据点作为初始大哥(质心,Centroid)
- 对集合中每一个小弟,计算与每一个大哥的距离(距离的含义后面会讲),离哪个大哥距离近,就跟定哪个大哥。
- 这时每一个大哥手下都聚集了一票小弟,这时候召开人民代表大会,每一群选出新的大哥(其实是通过算法选出新的质心)。
- 如果新大哥和老大哥之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止。
- 如果新大哥和老大哥距离变化很大,需要迭代3~5步骤。
例:
我搞了6个点,从图上看应该分成两推儿,前三个点一堆儿,后三个点是另一堆儿。现在手工执行K-Means,体会一下过程,同时看看结果是不是和预期一致。
case
1.选择初始大哥: 我们就选P1和P2
2.计算小弟和大哥的距离: P3到P1的距离从图上也能看出来(勾股定理),是√10 = 3.16;P3到P2的距离√((3-1)^2+(1-2)^2 = √5 = 2.24,所以P3离P2更近,P3就跟P2混。同理,P4、P5、P6也这么算,如下:
round1
P3到P6都跟P2更近,所以第一次站队的结果是:
- 组A:P1
- 组B:P2、P3、P4、P5、P6
3.人民代表大会: 组A没啥可选的,大哥还是P1自己 组B有五个人,需要选新大哥,这里要注意选大哥的方法是每个人X坐标的平均值和Y坐标的平均值组成的新的点,为新大哥,也就是说这个大哥是“虚拟的”。 因此,B组选出新大哥的坐标为:P哥((1+3+8+9+10)/5,(2+1+8+10+7)/5)=(6.2,5.6)。 综合两组,新大哥为P1(0,0),P哥(6.2,5.6),而P2-P6重新成为小弟
4.再次计算小弟到大哥的距离:
round2
这时可以看到P2、P3离P1更近,P4、P5、P6离P哥更近,所以第二次站队的结果是:
- 组A:P1、P2、P3
- 组B:P4、P5、P6(虚拟大哥这时候消失)
5.第二届人民代表大会: 按照上一届大会的方法选出两个新的虚拟大哥:P哥1(1.33,1) P哥2(9,8.33),P1-P6都成为小弟
6.第三次计算小弟到大哥的距离:
round3
这时可以看到P1、P2、P3离P哥1更近,P4、P5、P6离P哥2更近,所以第二次站队的结果是:
- 组A:P1、P2、P3
- 组B:P4、P5、P6
我们发现,这次站队的结果和上次没有任何变化了,说明已经收敛,聚类结束,聚类结果和我们最开始设想的结果完全一致。
K-Means的细节问题:
-
K值怎么定?我怎么知道应该几类? 答:这个真的没有确定的做法,分几类主要取决于个人的经验与感觉,通常的做法是多尝试几个K值,看分成几类的结果更好解释,更符合分析目的等。或者可以把各种K值算出的SSE做比较,取最小的SSE的K值。
-
初始的K个质心怎么选? 答:最常用的方法是随机选,初始质心的选取对最终聚类结果有影响,因此算法一定要多执行几次,哪个结果更reasonable,就用哪个结果。 当然也有一些优化的方法,第一种是选择彼此距离最远的点,具体来说就是先选第一个点,然后选离第一个点最远的当第二个点,然后选第三个点,第三个点到第一、第二两点的距离之和最小,以此类推。第二种是先根据其他聚类算法(如层次聚类)得到聚类结果,从结果中每个分类选一个点。
-
K-Means会不会陷入一直选质心的过程,永远停不下来? 答:不会,有数学证明K-Means一定会收敛,大致思路是利用SSE的概念(也就是误差平方和),即每个点到自身所归属质心的距离的平方和,这个平方和是一个函数,然后能够证明这个函数是可以最终收敛的函数。
-
判断每个点归属哪个质心的距离怎么算? 答:这个问题必须不得不提一下数学了…… 第一种,欧几里德距离(欧几里德这位爷还是很厉害的,《几何原本》被称为古希腊数学的高峰,就是用5个公理推导出了整个平面几何的结论),这个距离就是平时我们理解的距离,如果是两个平面上的点,也就是(X1,Y1),和(X2,Y2),那这俩点距离是多少初中生都会,就是√( (x1-x2)^2+(y1-y2)^2) ,如果是三维空间中呢?√( (x1-x2)^2+(y1-y2)^2+(z1-z2)^2 ;推广到高维空间公式就以此类推。可以看出,欧几里德距离真的是数学加减乘除算出来的距离,因此这就是只能用于连续型变量的原因。 第二种,余弦相似度,余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。下图表示余弦相似度的余弦是哪个角的余弦,A,B是三维空间中的两个向量,这两个点与三维空间原点连线形成的角,如果角度越小,说明这两个向量在方向上越接近,在聚类时就归成一类:
cos
看一个例子(也许不太恰当):歌手大赛,三个评委给三个歌手打分,第一个评委的打分(10,8,9) 第二个评委的打分(4,3,2),第三个评委的打分(8,9,10) 如果采用余弦相似度来看每个评委的差异,虽然每个评委对同一个选手的评分不一样,但第一、第二两个评委对这四位歌手实力的排序是一样的,只是第二个评委对满分有更高的评判标准,说明第一、第二个评委对音乐的品味上是一致的。 因此,用余弦相似度来看,第一、第二个评委为一类人,第三个评委为另外一类。 如果采用欧氏距离, 第一和第三个评委的欧氏距离更近,就分成一类人了,但其实不太合理,因为他们对于四位选手的排名都是完全颠倒的。 总之,如果注重数值本身的差异,就应该用欧氏距离,如果注重的是上例中的这种的差异(我概括不出来到底是一种什么差异……),就要用余弦相似度来计算。 还有其他的一些计算距离的方法,但是都是欧氏距离和余弦相似度的衍生,简单罗列如下:明可夫斯基距离、切比雪夫距离、曼哈顿距离、马哈拉诺比斯距离、调整后的余弦相似度、Jaccard相似系数……
-
还有一个重要的问题是,大家的单位要一致! 比如X的单位是米,Y也是米,那么距离算出来的单位还是米,是有意义的 但是如果X是米,Y是吨,用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方,最后算出的东西没有数学意义,这就有问题了。 还有,即使X和Y单位一致,但是如果数据中X整体都比较小,比如都是1到10之间的数,Y很大,比如都是1000以上的数,那么,在计算距离的时候Y起到的作用就比X大很多,X对于距离的影响几乎可以忽略,这也有问题。 因此,如果K-Means聚类中选择欧几里德距离计算距离,数据集又出现了上面所述的情况,就一定要进行数据的标准化(normalization),即将数据按比例缩放,使之落入一个小的特定区间。去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行计算和比较。 标准化方法最常用的有两种:
- min-max标准化(离差标准化):对原始数据进行线性变换,是结果落到【0,1】区间,转换方法为 X'=(X-min)/(max-min),其中max为样本数据最大值,min为样本数据最小值。
- z-score标准化(标准差标准化):处理后的数据符合标准正态分布(均值为0,方差为1),转换公式:X减去均值,再除以标准差
-
每一轮迭代如何选出新的质心? 答:各个维度的算术平均,比如(X1,Y1,Z1)、(X2,Y2,Z2)、(X3,Y3,Z3),那就新质心就是【(X1+X2+X3)/3,(Y1+Y2+Y3)/3,(Z1,Z2,Z3)/3】,这里要注意,新质心不一定是实际的一个数据点。
-
关于离群值? 答:离群值就是远离整体的,非常异常、非常特殊的数据点,在聚类之前应该将这些“极大”“极小”之类的离群数据都去掉,否则会对于聚类的结果有影响。但是,离群值往往自身就很有分析的价值,可以把离群值单独作为一类来分析。
-
用SPSS作出的K-Means聚类结果,包含ANOVA(单因素方差分析),是什么意思? 答:答简单说就是判断用于聚类的变量是否对于聚类结果有贡献,方差分析检验结果越显著的变量,说明对聚类结果越有影响。对于不显著的变量,可以考虑从模型中剔除。
聚类分析中业务专家的作用:
业务专家的作用非常大,主要体现在聚类变量的选择和对于聚类结果的解读:
- 比如要对于现有的客户分群,那么就要根据最终分群的目的选择不同的变量来分群,这就需要业务专家经验支持。如果要优化客户服务的渠道,那么就应选择与渠道相关的数据;如果要推广一个新产品,那就应该选用用户目前的使用行为的数据来归类用户的兴趣。算法是无法做到这一点的
- 欠缺经验的分析人员和经验丰富的分析人员对于结果的解读会有很大差异。其实不光是聚类分析,所有的分析都不能仅仅依赖统计学家或者数据工程师。
----------------------------------------------------------------------
上面的理论部分讲的很好,转载用来复习,下面这部分我利用Python实现了k-means算法:
看代码前线预览一下效果图
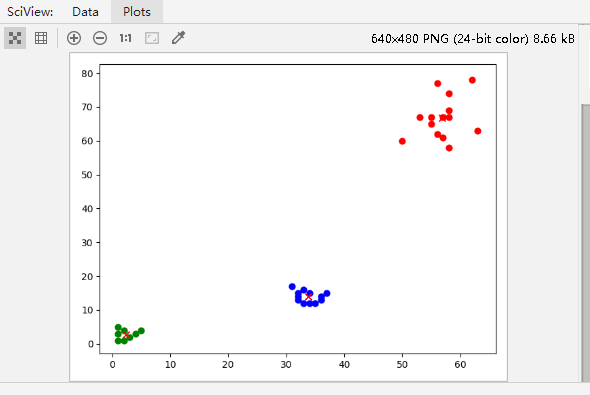
利用Python实现(不使用numpy、pandas)
import random
import matplotlib.pyplot as plt
import operator
# 创建数据集
def createDataSet():
dataset = []
for line in open("data.csv"):
x, y = line.split(",")
dataset.append([int(x), int(y)])
return dataset
# return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]
# k-means算法
def kmeans(dataSet, k):
center_cores = random.sample(dataSet, k)
# center_cores = [[1,2], [33,18], [50,70]]
print("随机质心:", center_cores)
changed, new_center_core = updateCenterCore2(dataSet, center_cores, k)
print("第1次改变量:", changed)
print("第1次新质心:", new_center_core)
c = 2
while changed != 0:
print("--------------------------------")
changed, new_center_core = updateCenterCore2(dataSet, new_center_core, k)
print(c, "改变量:", changed)
print(c, "新质心:", new_center_core)
c = c + 1
return changed, new_center_core
# 更新质心
def updateCenterCore(dataSet, centerCores, k):
# 求各点到质心的距离
calc_dis_list = calcDis(dataSet, centerCores, k)
new_center_cores = []
print(calc_dis_list)
# 求新的质心
l = len(dataSet)
'''
对个点进行分类,分到对应质点下面
比较每个点对各个质点的距离,然后把各个点分到对应的质点簇,然后进行质点更新
'''
classfiy = []
x = []
for j in range(k):
classfiy.append([])
for i in range(l):
min_val = calc_dis_list[i]
min_indx = i
t = i
for j in range(k - 1):
if min_val > calc_dis_list[t + l]:
min_val = calc_dis_list[t + l]
min_indx = t + l
t = t + l
classfiy[min_indx // l].append(dataSet[i])
print(classfiy)
print("----------------------------------")
for i in range(k):
minX = 0
minY = 0
for j in range(len(classfiy[i])):
minX = minX + classfiy[i][j][0]
minY = minY + classfiy[i][j][1]
# print(minX / len(classfiy[i]), minY / len(classfiy[i]))
if len(classfiy[i]) == 0:
new_center_cores.append(centerCores[i])
else:
new_center_cores.append([minX / len(classfiy[i]), minY / len(classfiy[i])])
print("新质心为:", new_center_cores)
changed = 0
for i in range(k):
changed = changed + (((new_center_cores[i][0] - centerCores[i][0]) ** 2 + (
new_center_cores[i][1] - centerCores[i][1]) ** 2) ** 0.5)
return changed, new_center_cores
# 更新质心
def updateCenterCore2(dataSet, centerCores, k):
# 求各点到质心的距离
calc_dis_list = calc_point2centers(dataSet, centerCores, k)
new_center_cores = []
print(calc_dis_list)
# 求新的质心
l = len(dataSet)
'''
对个点进行分类,分到对应质点下面
比较每个点对各个质点的距离,然后把各个点分到对应的质点簇,然后进行质点更新
'''
classfiy = []
x = []
for j in range(k):
classfiy.append([])
for i in range(l):
min_val = calc_dis_list[i][0]
class_index = 0
for j in range(1, k):
if min_val > calc_dis_list[i][j]:
min_val = calc_dis_list[i][j]
class_index = j
classfiy[class_index].append(dataSet[i])
print(classfiy)
print("----------------------------------")
for i in range(k):
minX = 0
minY = 0
for j in range(len(classfiy[i])):
minX = minX + classfiy[i][j][0]
minY = minY + classfiy[i][j][1]
# print(minX / len(classfiy[i]), minY / len(classfiy[i]))
if len(classfiy[i]) == 0:
new_center_cores.append(centerCores[i])
else:
new_center_cores.append([minX / len(classfiy[i]), minY / len(classfiy[i])])
print("新质心为:", new_center_cores)
changed = 0
for i in range(k):
changed = changed + (((new_center_cores[i][0] - centerCores[i][0]) ** 2 + (
new_center_cores[i][1] - centerCores[i][1]) ** 2) ** 0.5)
return changed, new_center_cores
# 计算各点到质心的距离
def calcDis(dataSet, centerCores, k):
calcList = []
for j in range(k):
for i in range(len(dataSet)):
calcList.append(
(((centerCores[j][0] - dataSet[i][0]) ** 2 + (centerCores[j][1] - dataSet[i][1]) ** 2) ** 0.5))
# print("各点与质心的距离:",calcList)
return calcList
# 计算距离
def calc_dis(point, center):
return (((center[0] - point[0]) ** 2 + (center[1] - point[1]) ** 2) ** 0.5)
# 计算各节点到各质心的距离并放入calcList列表
def calc_point2centers(dataset, centerCores, k):
calcList = []
for i in range(len(dataset)):
calcList.append([])
for j in range(k):
calcList[i].append((calc_dis(dataset[i], centerCores[j])))
return calcList
if __name__ == '__main__':
startList = createDataSet()
for i in range(len(startList)):
plt.scatter(startList[i][0], startList[i][1], marker='o', color='green', s=40, label='原始点')
print("原始数据点:", startList)
changed, new_center_cores = kmeans(startList, 3)
for i in range(len(new_center_cores)):
plt.scatter(new_center_cores[i][0], new_center_cores[i][1], marker='x', color='red', s=50, label='质心')
plt.show()
利用Python实现(使用numpy、pandas)
import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt
def createDataSet():
dataset = []
for line in open("data.csv"):
x, y = line.split(",")
dataset.append([int(x), int(y)])
return dataset
# return [[1, 1], [1, 2], [2, 1], [6, 4], [6, 3], [5, 4]]
def kmeans(dataSet, k):
# 随机取质心
center_cores = random.sample(dataSet, k)
print("随机质心为:", center_cores)
# 更新质心 直到变化量全为0
changed, new_center_core = updateCenterCore(dataSet, center_cores, k)
print("第1次改变量:", changed)
print("第1次新质心:", new_center_core)
c = 2
while np.any(changed != 0):
print("--------------------------------")
changed, new_center_core = updateCenterCore(dataSet, new_center_core, k)
print(c, "改变量:", changed)
print(c, "新质心:", new_center_core)
c = c + 1
# 根据质心计算每个集群
cluster = []
clalist = calcDis(dataSet, new_center_core, k) # 调用欧拉距离
# print("fnjsanvjd:",clalist)
minDistIndices = np.argmin(clalist, axis=1)
print("minDistIndices:",minDistIndices)
for i in range(k):
cluster.append([])
for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素
cluster[j].append(dataSet[i])
# print(i,j)
# print("mmasdognjangosanmkjldk:",cluster)
return cluster, new_center_core
def calcDis(dataSet, center_cores, k):
clalist = []
# print(dataSet[1], center_cores[1])
for data in dataSet:
diff = np.tile(data, (k,
1)) - center_cores # 相减 (np.tile(a,(2,1))就是把a先沿x轴复制1倍,即没有复制,仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))
squaredDiff = diff ** 2 # 平方
squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行,按行相加)
distance = squaredDist ** 0.5 # 开根号
clalist.append(distance)
# print("clalist:", clalist)
clalist = np.array(clalist) # 返回一个每个点到质点的距离len(dateSet)*k的数组
# print("np.array(clalist):", clalist)
return clalist
def updateCenterCore(dataSet, center_cores, k):
# 计算样本到质心的距离
clalist = calcDis(dataSet, center_cores, k)
# 分组并计算新的质心
minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标
new_center_core = pd.DataFrame(dataSet).groupby(
minDistIndices).mean() # DataFramte(dataSet)对DataSet分组,groupby(min)按照min进行统计分类,mean()对分类结果求均值
new_center_core = new_center_core.values
# 计算变化量
changed = new_center_core - center_cores
return changed, new_center_core
if __name__ == '__main__':
start_list = createDataSet()
# for i in range(len(start_list)):
# plt.scatter(start_list[i][0], start_list[i][1], marker='o', color='green', s=40, label='原始点')
# print("原始数据点:", start_list)
cluster, new_center_cores = kmeans(start_list, 3)
color = ['green', 'red', 'blue']
count = 0
for zu in cluster:
for j in zu:
plt.scatter(j[0], j[1], marker='o', color=color[count], s=40, label='原始点')
count = count+1
for i in range(len(new_center_cores)):
plt.scatter(new_center_cores[i][0], new_center_cores[i][1], marker='x', color='red', s=50, label='质心')
# print("计算结果为:",cluster, new_center_cores)
plt.show()
代码和相关数据已经上传github:上面代码点击这里


