「XSection立体几何」中心投影和平行投影

投影

话说前几天我在翻北师大版九年级上册数学书时，发现这本书的第五章是“投影与视图”。（这游戏没有汉化，这使书上术语的英文名是我感到十分亲切。。）

这一章的第一小节就是投影，但其实对于立体几何，书上讲得非常简单，这节的重点其实是承接上一章《图形的相似》，利用相似三角形来计算投影的位置。

即使是这样，我觉得还是很有必要放一下教科书上对投影的定义的：

物体在光线的照射下，会在地面或其他平面上留下它的影子，这就是投影（Projection）现象，影子所在的平面称为投影面。

本来，小编觉得这句话的前半句太过物理化，不像数学语言的风格。但我之后又发现 百度百科 和 Wikipedia 上都是差不多的解释，也就认了这个定义。

直到我翻了翻 XSection 的术语表：

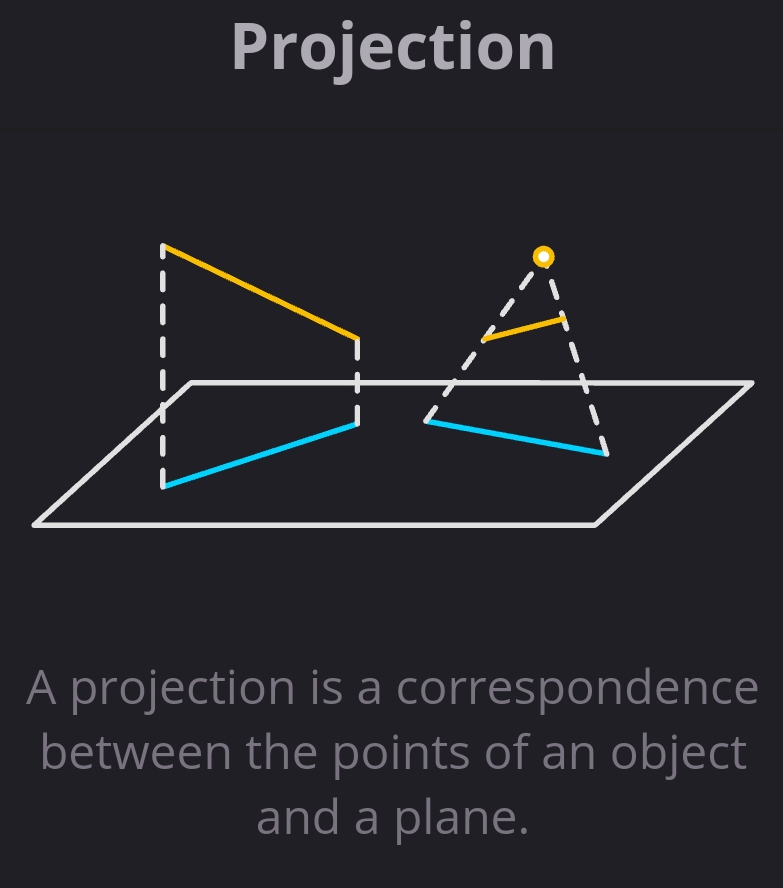
它的解释是这样的：

A projection is a correspondence between the points of an object and a plane.

翻译成中文就是：

投影是对象上和平面之间点的的对应关系

其中，correspondence这个词就用得非常妙，一开始我其它词都认识，只有这个不知道什么意思，之后上谷歌翻译查了查，Google 给我的解释是 “对应”。

我认为这个术语表中的解释是非常到位的，至少在游戏中是适用且非常严谨的。

在后面的关卡中，会有许多需要找出投影的任务，这类题无非分两种，一种是已知平面上的投影，求物体（object）上的点。

一种是已知物体上的点，求它在已知平面上的投影。

而只要掌握了这种对应关系，这两种问题都可以迎刃而解。

中心投影

按照数学书对投影的解释，把光源看作是一个点，也就是所有的光线都会相交在一个点上，就是中心投影。

数学书上的定义如下：

手电筒、路灯和台灯的光线可以看成是从一个点发出的，这样的光线所形成的投影称为中心投影。

最典型的例子就是灯泡了，我们可以将它看作是一个点光源，会向各个方向发光。手电筒还并不是一个典型，因为许多手电筒发出的其实更像是平行光。

在 XSection 中，它的定义是这样的：

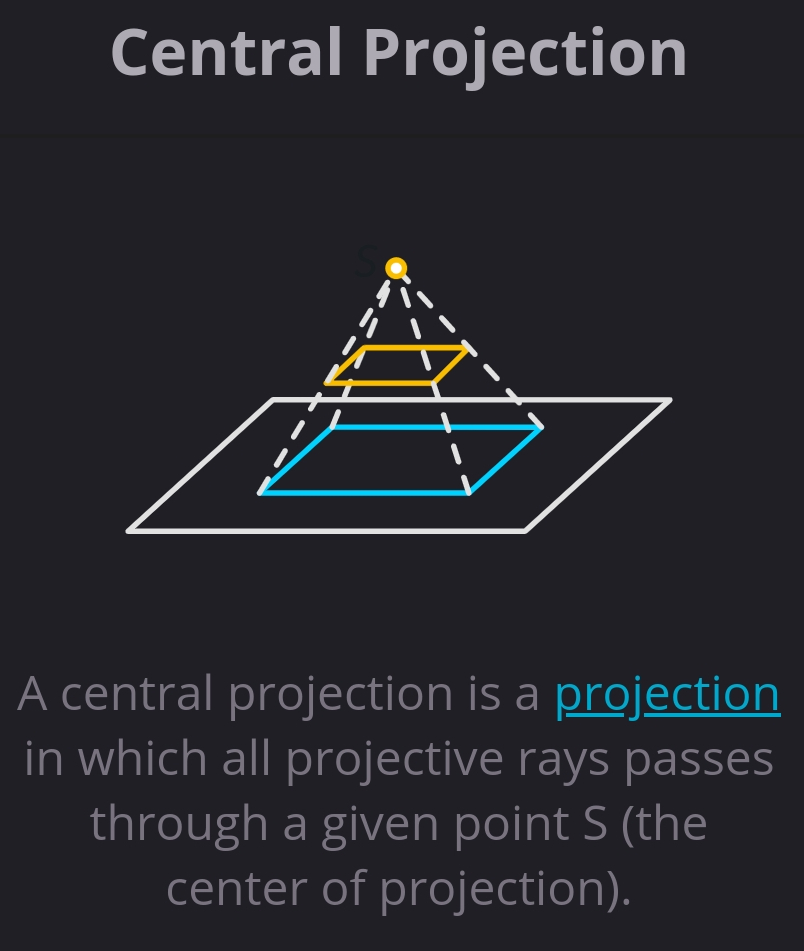
A central projection is a projection in which all projective rays passes through a given point S (the center of projetion).

翻译过来就是：

中心投影中的每个投射线经过一个已知的点S（投影中心）。

平行投影

对于平行投影，一个很有意思的点是，太阳和灯都在向各个方向发光，但人们一般把灯光看作是点光源，使用的是中心投影，而太阳光则是平行光线，使用平行投影。

这主要是因为，太阳离我们太远了，物体上的任意两个点与太阳构成的三角形的那个角实在太小太小了，完全可以看作是平行的。

对于平行投影，书上的定义是这样的：

太阳光线可以看成平行光线，平行光线所形成的投影成为平行投影（parallel projeciton）.

百度百科上说：

如果把中心投影法的投射中心即光源S移至无穷远处，则各投射线成为相互平行的直线，物体投影就不受距离变化的影响，这种投射线都互相平行的投影法称为平行投影法。

而 XSection 上的定义，则更加严谨和明确：

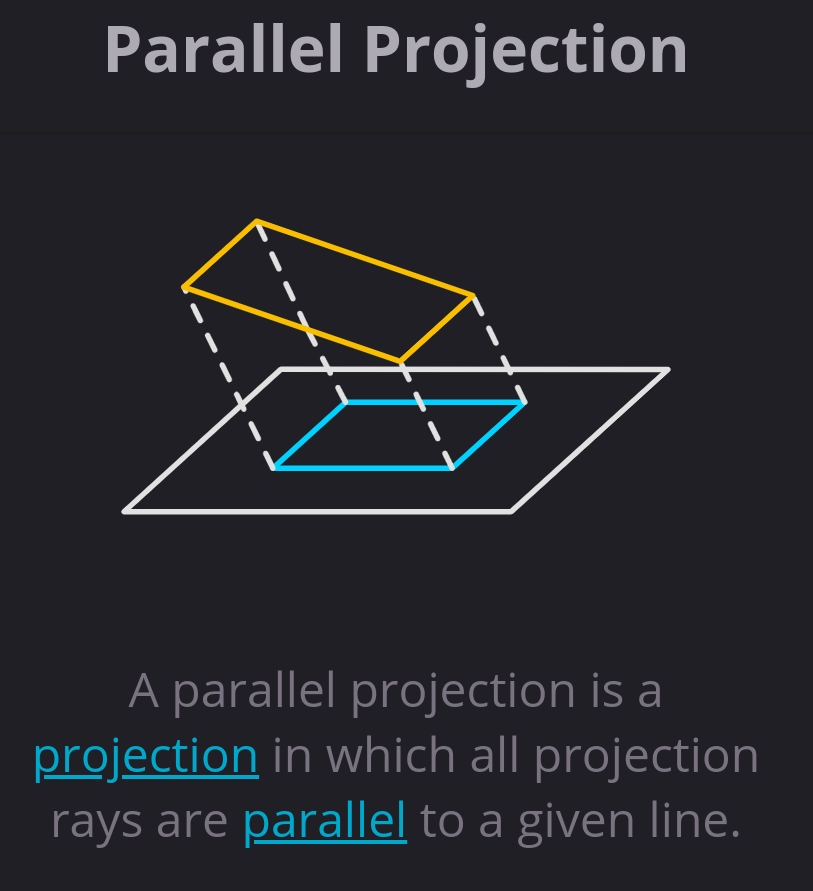
A parallel projection is a projection in which all projection rays are parallel to a given line.

翻译成中文就是：

平行投影指的是每一条投射线都与给定直线平行的投影。

一个例子

值得注意的是，在游戏中，所有关于投影的题都不会提示你使用中心投影法或者平行投影法。

不知道各位有没有发现，在画图上，平行投影法像是画出了一个棱柱，而中心投影法像是画出了一个棱锥。

这是因为棱柱的每条棱互相平行，正好符合平行投影中投射线的性质。棱锥中所有棱都会相交与一点，也符合中心投影的性质。

下面来看一个例子。因为 XSection 中是无法改变视图的，再加上竖屏不方便观看，我们就用 GeoGebra 进行演示：

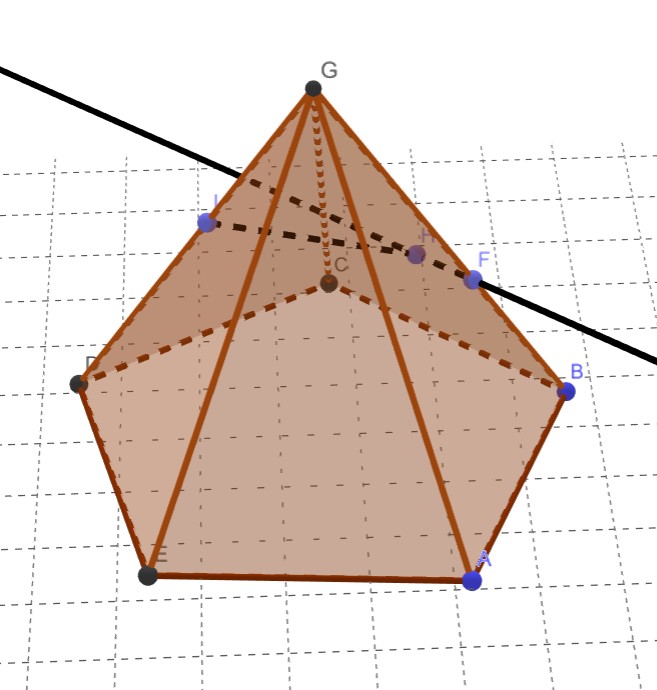
这是 XSection 中的 3.4 题，我认为比较有代表性。题目是这样的：

已知I、H两点，求线段 I、H 在底面上的投影。（过F点的直线FH和GC是相交的，原谅我忘了作交点了吧）

看到这个棱锥，首先想到的一定是中心投影法，因为它相当于给定了一个点G来求投影。

投影面当然是底面，这个在题目中有提到。

需要说明的是，直线FH的作用是表明点H在平面BGC上。事实上，FH//BC。

那么作法就非常简单了，首先连接并延长GH、GI。

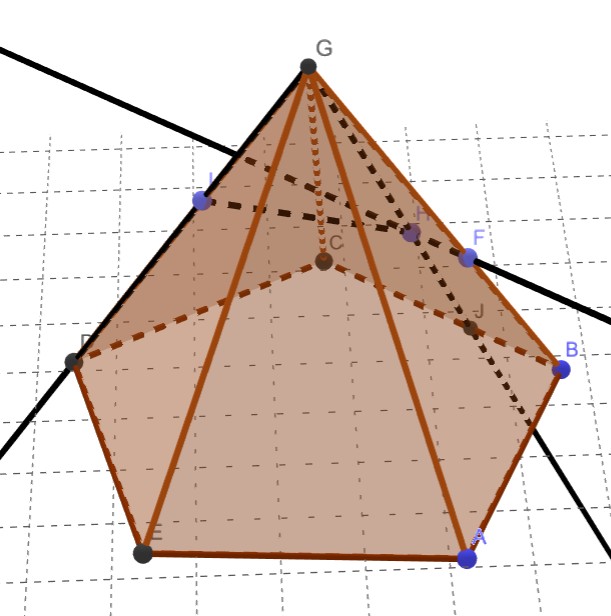
下一步，找到这两条射线和底面的交点。

这里要注意的是，游戏中你是无法直接找到线和面的交点的，必须找到这个面上可以与它相交的一条线，然后点出线与线的交点（这其实也是后面很多题的难点）

在这道题中，这条线就是BC。第一节中讲过，「一个平面上任意个点都是处在同一平面的」，所以，有了平面BCG，就有平面HCG，也就有交点J。

于是，根据同样的方法，可以找到点I的投影点D。

最后，连接DJ，完成。

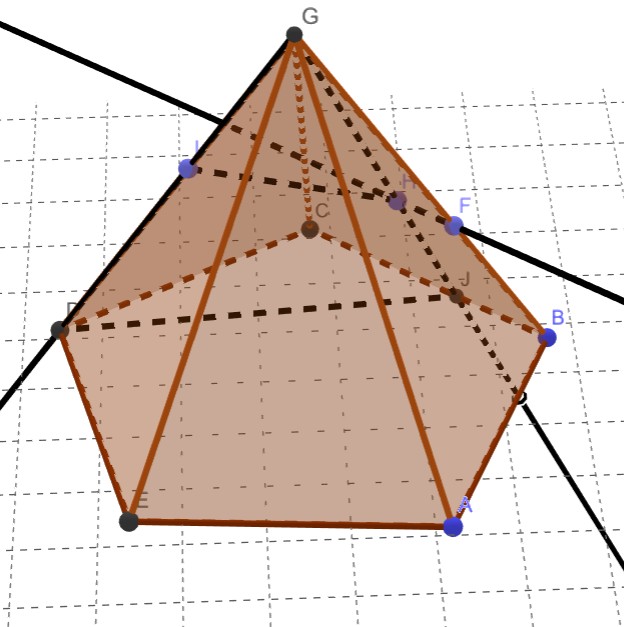
-> to be continued...