「CH0601」Genius ACM

题目链接 & 题面

AcWing：https://www.acwing.com/problem/content/description/111/

ContestHunter 挂了，只有 AcWing 上能找到这题了。。

题目描述

给定一个整数 M，对于任意一个整数集合 S，定义“校验值”如下:

从集合 S 中取出 M 对数(即 2∗M个数，不能重复使用集合中的数，如果 S 中的整数不够 M 对，则取到不能取为止)，使得“每对数的差的平方”之和最大，这个最大值就称为集合 S 的“校验值”。

现在给定一个长度为 N 的数列 A 以及一个整数 T。

我们要把 A 分成若干段，使得每一段的“校验值”都不超过 T。

求最少需要分成几段。

输入格式

第一行输入整数 K，代表有 K 组测试数据。

对于每组测试数据，第一行包含三个整数 N,M,T 。

第二行包含 N 个整数，表示数列A1,A2…AN。

输出格式

对于每组测试数据，输出其答案，每个答案占一行。

数据范围

1≤K≤12,
1≤N,M≤500000,
0≤T≤10^18,
0≤Ai≤2^20

基本思路

朴素算法——暴力

从这个集合的开头开始，确定每一个划分点。

采用类似贪心的方法，不考虑后面的数， 一个个向后枚举划分点。

拿样例数据举例：

2
5 1 49
8 2 1 7 9
5 1 64
8 2 1 7 9

先规定起始点 l 为 0，然后枚举：

{8} -> {8, 2} -> {8, 2, 1} -> {8, 2, 1, 7} -> {8, 2, 1, 7, 9} ->{8, 2, 1, 7}, {9}

每次枚举还需要 O(n lg n) 的时间来排序，时间复杂度为 O(n^2 lg n)

倍增（其实有点像二分）

把枚举改成倍增

显而易见，对于相同的左端 l，右端 r 越大，校验值越大（也有可能相等）。

所以，校验值可以看成是具有单调性的，可以通过倍增求解。

具体来说，可以确定一个右端 R 和右端增加长度 p，如果这个序列的校验值小于等于上限，那么将 p 乘以 2，并且将右端更新（R+=p），如果大于上限，就将 p 除以 2。

这样，我们可以将时间复杂度降低到 O(n^2)

关于排序

每次求校验值时都需要排序，其实没有必要使用快速排序，可以采用归并排序，把新增的序列排好序然后再归并。时间复杂度 O(n lg n)

然而我用了时间复杂度相同的二分插入排序，但是后面 TLE 了，时间限制是10s，我的程序运行了600s

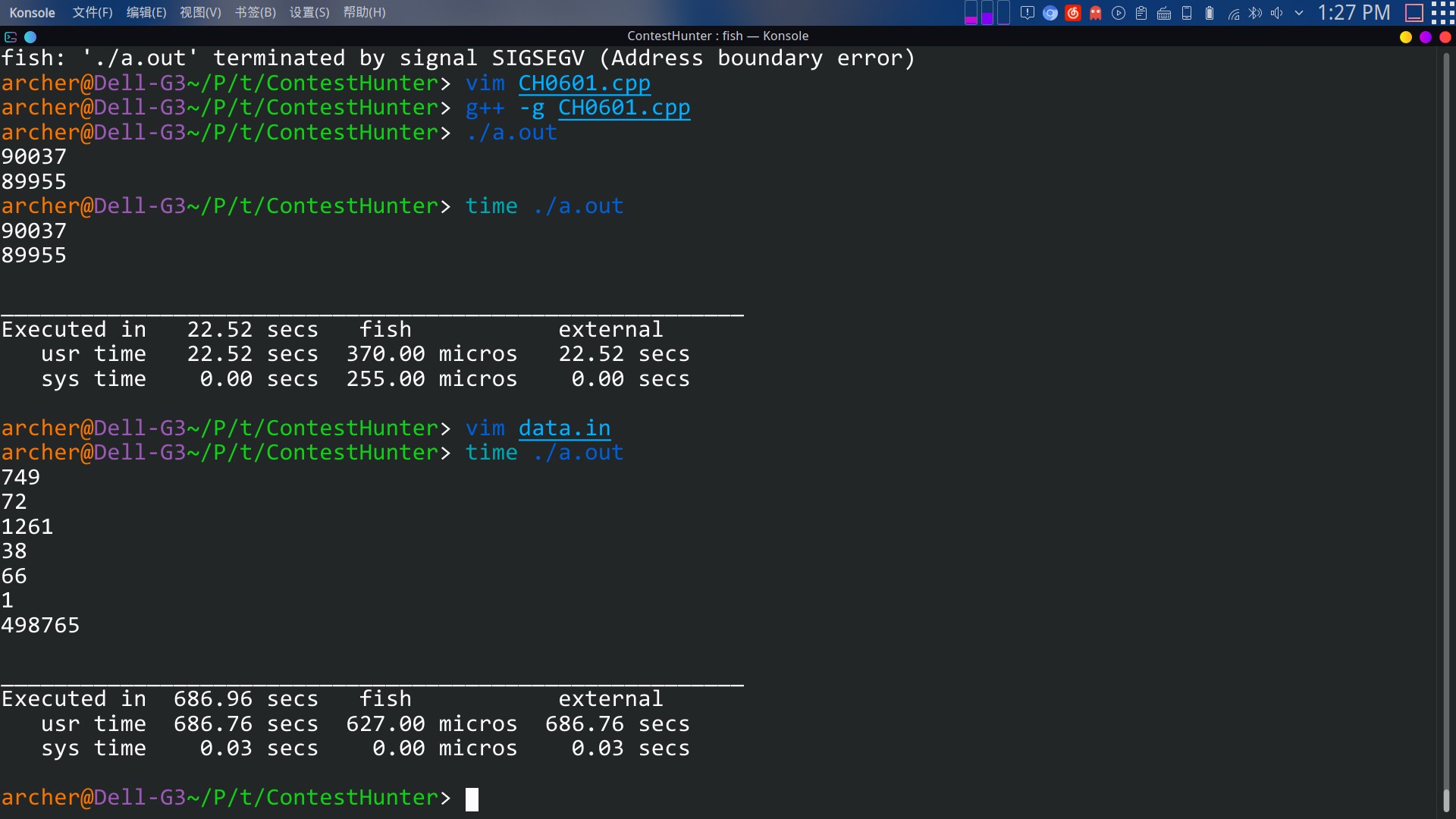
应该是 vector 常数太大了吧

代码

#include <cstdio>
#include <iostream>
#include <vector>
using std::vector;
using std::min;

const int MAX=500005;
int k, n, m;
vector<long long> o, ne;
long long t, a[MAX];

int genius(void);
long long check(int, int);

int main(){
	freopen("data.in", "r", stdin);
	
	scanf("%d", &k);
	for(int i=0; i<k; i++){
		scanf("%d%d%lld", &n, &m, &t);
		for(int i=0; i<n; i++){
			scanf("%lld", &a[i]);
		}
		printf("%d\n", genius());
	}
	
	return 0;
}

int genius(){
	int r=0, ans=0, l, p;
	long long ch;
	while(r<n){
		if(r==n-1){
			ans++; break;
		}
		l=r; p=1;
		ne.clear(); o.clear();
		while(p!=0 && r<n){
			ch = check(r, p);
			if(ch<=t){
				r+=p; p*=2;
				o=ne;
			}
			else p/=2;
		}
		ans++;
	}
	return ans;
}

long long check(int r, int p){
	ne=o;
	int l, r1, mid;
	for(int i=r; i<min(r+p, n); i++){
		l=0; r1=ne.size();
		while(l<r1){
			mid=(l+r1)>>1;
			if(ne[mid]>=a[i]) r1=mid; 
			else l=mid+1;
		}
		ne.insert(ne.begin()+l, a[i]);
	}
	int s=ne.size();
	long long ans=0;
	for(int i=0; i<m; i++){
		if(s>=(i+1)*2){
			ans+=(ne[i]-ne[s-i-1])*(ne[i]-ne[s-i-1]);
		}
	}
	return ans;
}