面试总结1
1、http和https区别
2、MySQL隔离级别
3、linux基础命令
4、PHP魔术方法
5、php7新特性
6、MySQL分区分表
7、MySQL索引原理及查询优化
8、nginx实现负载均衡
9、nginx实现反向代理
10、反射与映射
11、redis
12、进程与线程
13、进程调度
14、MySQL常用数据类型
15、三次握手和四次挥手
16、PHP实现原理
17、设计一个排名榜的设计方案
18、abcde求子集,必须要包含全部字母,不能有重复
19、阶乘算法
20、12345求子集
21、编写shell脚本,读取 ./path 目录下所有 .data文件
22、二叉树的层级查找
23、B树和B+树
答案:
2、MySQL事物及隔离级别:
事物的基本要素:
①原子性(Atomicity):事务开始后所有操作,要么全部做完,要么全部不做,不可能停滞在中间环节。事务执行过程中出错,会回滚到事务开始前的状态,所有的操作就像没有发生一样。也就是说事务是一个不可分割的整体,就像化学中学过的原子,是物质构成的基本单位。
②一致性(Consistency):事务开始前和结束后,数据库的完整性约束没有被破坏 。比如A向B转账,不可能A扣了钱,B却没收到。
③隔离性(Isolation):同一时间,只允许一个事务请求同一数据,不同的事务之间彼此没有任何干扰。比如A正在从一张银行卡中取钱,在A取钱的过程结束前,B不能向这张卡转账。
⑤持久性(Durability):事务完成后,事务对数据库的所有更新将被保存到数据库,不能回滚。
隔离级别:
①脏读(未提交读):事务A读取了事务B更新的数据,然后B回滚操作,那么A读取到的数据是脏数据
②提交读(不可重复读):事务 A 多次读取同一数据,事务 B 在事务A多次读取的过程中,对数据作了更新并提交,导致事务A多次读取同一数据时,结果 不一致。
③幻读(可重复读):系统管理员A将数据库中所有学生的成绩从具体分数改为ABCDE等级,但是系统管理员B就在这个时候插入了一条具体分数的记录,当系统管理员A改结束后发现还有一条记录没有改过来,就好像发生了幻觉一样,这就叫幻读。
④可串行化:是最高的隔离级别。它通过强制事物串行执行,避免了前面说的幻读问题。简单来说,serializable会在读取的每一行数据上都加锁,所以可能导致大量的超市和锁争用的问题。实际应用中也很少用到这个隔离级别,只有在非常需要确保数据的一致性而且可以接受没有并发的情况下,才考虑采用该级别。
3、linux基础命令
4、PHP魔术方法:
__construct(),类的构造函数
__destruct(),类的析构函数
__call(),在对象中调用一个不可访问方法时调用
__callStatic(),用静态方式中调用一个不可访问方法时调用
__get(),获得一个类的成员变量时调用
__set(),设置一个类的成员变量时调用
__isset(),当对不可访问属性调用isset()或empty()时调用
__unset(),当对不可访问属性调用unset()时被调用。
__sleep(),执行serialize()时,先会调用这个函数
__wakeup(),执行unserialize()时,先会调用这个函数
__toString(),类被当成字符串时的回应方法
__invoke(),调用函数的方式调用一个对象时的回应方法
__set_state(),调用var_export()导出类时,此静态方法会被调用。
__clone(),当对象复制完成时调用
__autoload(),尝试加载未定义的类
__debugInfo(),打印所需调试信息
实例:参见详情
6、MySQL分区分表:mysql分表分库策略;
7、MySQL索引原理及查询优化:MySQL查询优化
8:nginx实现负载均衡:负载均衡算法;nginx实现负载均衡与缓存;nginx负载均衡与反向代理;
9:nginx实现反向代理:使用nginx实现反向代理
10:反射与映射:Java反射和映射
11:redis:redis面试;redis和memcache
13、进程调度:
①先来先服务
②短作业优先
③高优先权优先调度算法
④高响应比优先调度算法
⑤基于时间片的轮转
⑥多级反馈队列调度算法
14:MySQL常用数据类型
①整数
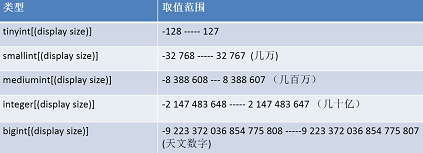
②【定数】小数:decimal(dec)精确小数类型---精确数的存储
③浮点数:float/double单精度、双精度浮点类型········
④字符串:
char(n):固定长度,最多255个字符
varchar(n):固定长度,最多65535个字符
tinytext:可变长度,最多255个字符
text:可变长度,最多65535个字符
mediumtext:可变长度,最多2的24次方-1个字符
longtext:可变长度,最多2的32次方-1个字符
⑤日期时间时区:
date:日期 '2008-12-02'
time:时间 '12:25:36'
datetime:日期时间 '2008-12-12 22:06:44'
timestamp:自动存储记录修改时间(如果数据库里面有timestamp数据类型,就应该考虑时区问题)
15:三次握手和四次挥手:TCP/IP协议
16、PHP实现原理
17:设计一个排名榜的设计方案
18:abcde求子集,必须要包含全部字母,不能有重复
function func2($arr, $str){ // $str 为保存由 i 组成的一个排列情况
$cnt = count($arr);
if($cnt == 1){
echo $str . $arr[0] . "\n<br>";
} else {
for ($i = 0; $i < count($arr); $i++) {
$tmp = $arr[0];
$arr[0] = $arr[$i];
$arr[$i] = $tmp;
func2(array_slice($arr, 1), $str . $arr[0]);
}
}
}
$a = array('1', '2', '3', '4');
func2($a, '');
19:阶乘算法
方案一之递归:
private static long RecursiveFac(long n){
if (n == 0){
return 1;
}else{
return n * RecursiveFac(n - 1);
}
}
方案二之递推:
private static long Fac(long n){
var result = 1;
for (var i = 1; i <= n; i++){
result = result * i;
}
return result;
}
方案三之尾递归:
private static int TailRecursiveFac(int n, int accumulator){
if (n == 0){
return accumulator;
}
return Fac(n - 1, n * accumulator);
}
方案四之消除尾递归:
private static int Fac(int n, int accumulator){
while (true){
var tempN = n;
var tempAccumulator = accumulator;
if (tempN == 0){
return tempAccumulator;
}
n = tempN - 1;
accumulator = tempN * tempAccumulator;
}
}
20:12345求子集
public static List<List<Integer>> rank(int[] nums){ List<Integer>source = new ArrayList<>(); for (int i = 0; i < nums.length; i++) { source.add(nums[i]); } List<List<Integer>> res = new ArrayList<>(); for (int i = 0; i < source.size(); i++) { List<Integer> tem = new ArrayList<>(); tem.add(source.get(i)); if (res.size()>0){ List<List<Integer>> in = new ArrayList<>(); for (List<Integer> re : res) { List<Integer> temp = new ArrayList<>(tem); temp.addAll(re); in.add(temp); } res.addAll(in); } res.add(tem); } res.add(new ArrayList<>()); return res; }
21、编写shell脚本,读取 ./path 目录下所有 .data文件
22、二叉树的层级查找
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public static void LaywerTraversal(TreeNode root){
if(root==null) {
return;
}
LinkedList<TreeNode> list = new LinkedList<TreeNode>();
list.add(root);
TreeNode currentNode;
while(!list.isEmpty()){
currentNode=list.poll();
System.out.println(currentNode.val);
if(currentNode.left!=null){
list.add(currentNode.left);
}
if(currentNode.right!=null){
list.add(currentNode.right);
}
}
}
23、B树即二叉树:
为什么B树可以优化查询:为什么B类树可以进行优化呢?我们可以根据B类树的特点,构造一个多阶的B类树,然后在尽量多的在结点上存储相关的信息,保证层数尽量的少,以便后面我们可以更快的找到信息,磁盘的I/O操作也少一些,而且B类树是平衡树,每个结点到叶子结点的高度都是相同,这也保证了每个查询是稳定的。
这里的B树,也就是英文中的B-Tree,一个 m 阶的B树满足以下条件:
- 每个结点至多拥有m棵子树;
- 根结点至少拥有两颗子树(存在子树的情况下);
- 除了根结点以外,其余每个分支结点至少拥有 m/2 棵子树;
- 所有的叶结点都在同一层上;
- 有 k 棵子树的分支结点则存在 k-1 个关键码,关键码按照递增次序进行排列;
- 关键字数量需要满足ceil(m/2)-1 <= n <= m-1;
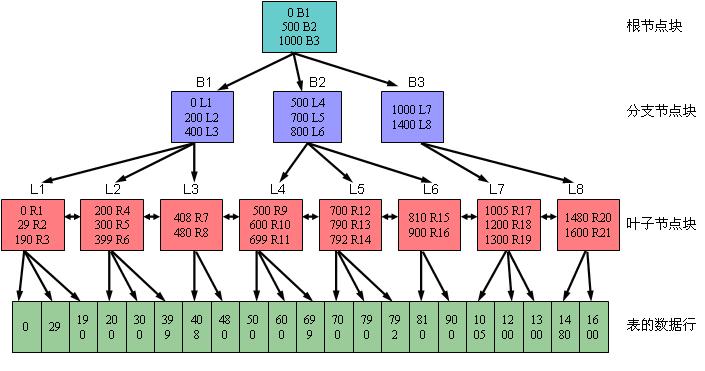
B树上大部分的操作所需要的磁盘存取次数和B树的高度是成正比的,在B树中可以检查多个子结点,由于在一棵树中检查任意一个结点都需要一次磁盘访问,所以B树避免了大量的磁盘访问。
为什么需要B+树:由于B+树的数据都存储在叶子结点中,分支结点均为索引,方便扫库,只需要扫一遍叶子结点即可,但是B树因为其分支结点同样存储着数据,我们要找到具体的数据,需要进行一次中序遍历按序来扫,所以B+树更加适合在区间查询的情况,所以通常B+树用于数据库索引,而B树则常用于文件索引。
以一个m阶树为例:
- 根结点只有一个,分支数量范围为[2,m];
- 分支结点,每个结点包含分支数范围为[ceil(m/2), m];
- 分支结点的关键字数量等于其子分支的数量减一,关键字的数量范围为[ceil(m/2)-1, m-1],关键字顺序递增;
- 所有叶子结点都在同一层;
B树和B+树的区别:
这都是由于B+树和B具有这不同的存储结构所造成的区别,以一个m阶树为例。
- 关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
- 存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
- 分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
- 查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。
扩展:
获取树的深度:
class Bitree {
int data;
Bitree left;
Bitree right;
}
private static int BitreeDepth(Bitree p) {
int rd,ld;
if(p == null){
return 0;
}else{
ld=BitreeDepth(p.left);
rd=BitreeDepth(p.right);
if(ld>rd){
return ld+1;
}else {
return rd+1;
}
}
}
求e在二叉树P中的层次。如果不存在返回值为0;否则返回值为层次
class Bitree {
int data;
Bitree left;
Bitree right;
}
private static int BitreeLevel(Bitree P,char e) {
int ld=0;
int rd=0;
if(P == null){
return 0;
}else if(e==P.data){
return 1;
}else if(e!=P.data) {
ld=BitreeLevel(P.left,e);
rd=BitreeLevel(P.right,e);
if(ld>0){
return ld+1;
}else if(rd>0){
return rd+1;
}else {
return 0;
}
}
return ld>rd?ld:rd;
}





