C++常见算法总结

堆排序学习

bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
 
      return lhs.second > rhs.second;    //小顶堆
}
 
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;
 
 
    //完整版按大堆创建对象
    //priority_queue<int,vector<int>, less<int>> q;
 
    //按小堆创建对象(按小堆创建时参数列表不可以省略)
    //priority_queue<int,vector<int>, greater<int>> q;
 
 
 
    //简化版按大堆创建对象
    //默认创建大堆
priority_queue<int> q(arr, arr + sizeof(arr) / sizeof(arr[0]));

参考资料

C++ 优先队列 priority_queue 使用篇_爱喝酸奶！的博客-CSDN博客

C++-STL-priority_queue（堆/优先队列）的简单使用_哔哩哔哩_bilibili

股票问题

买卖股票的最佳时机

只能买卖一次

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
 
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
 
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
 
示例 1：
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
 
示例 2：
输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

#include <vector>
#include <iostream>
using namespace std;
 
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len,vector<int>(2,0));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++)
        {
            dp[i][0] = max(dp[i-1][0],-prices[i]);
            dp[i][1] = max(dp[i-1][0] + prices[i],dp[i-1][1]);
        }
 
        return dp[len-1][1];
    }
};

买卖股票的最佳时机 II

可以多次无限买卖

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
 
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。
 
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
 
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
 
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
 
提示：
 
1 <= prices.length <= 3 * 10 ^ 4
0 <= prices[i] <= 10 ^ 4

#include <vector>
#include <iostream>
using namespace std;
 
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        int len = prices.size();
        vector<vector<int>> dp(len,vector<int>(2,0));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++)
        {
            dp[i][0] = max(dp[i-1][0],-prices[i] + dp[i-1][1]);
            dp[i][1] = max(dp[i-1][1],prices[i] + dp[i-1][0]);
        }
 
        return dp[len-1][1];
 
 
    }
};

买卖股票的最佳时机 III

最多完成两次交易

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。
 
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
 
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
示例 1: 输入：prices = [3,3,5,0,0,3,1,4] 输出：6 解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3。
 
示例 2： 输入：prices = [1,2,3,4,5] 输出：4 解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。
 
示例 3： 输入：prices = [7,6,4,3,1] 输出：0 解释：在这个情况下, 没有交易完成, 所以最大利润为0。
 
示例 4： 输入：prices = [1] 输出：0
 
提示：
 
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^5

一天一共就有五个状态

没有操作
第一次买入
第一次卖出
第二次买入
第二次卖出

#include <vector>
using namespace std;
 
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len,vector<int>(5,0));
        dp[0][1] = -prices[0];
        dp[0][2] = 0;
        dp[0][3] = -prices[0];
        dp[0][4] = 0;
 
        for (int i = 1; i < len; i++)
        {
            dp[i][1] = max(dp[i-1][1],-prices[i]);
            dp[i][2] = max(dp[i-1][2],dp[i-1][1] + prices[i]);
            dp[i][3] = max(dp[i-1][3],dp[i-1][2] - prices[i]);
            dp[i][4] = max(dp[i-1][4],dp[i-1][3] + prices[i]);
        }
        return dp[len-1][4];
    }
};

买卖股票的最佳时机 IV

最多完成K笔交易

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
 
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
 
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
示例 1： 输入：k = 2, prices = [2,4,1] 输出：2 解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2。
 
示例 2： 输入：k = 2, prices = [3,2,6,5,0,3] 输出：7 解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
 
提示：
 
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000

#include <vector>
using namespace std;
 
class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len,vector<int>(2*k+1,0));
        //初始化
        for (int i = 0; i < k; i++)
        {
            dp[0][2*i+1] = -prices[0];
        }
 
        //开始递归
        for (int i = 1; i < len; i++)
        {
            for (int j = 1; j <2*k+1; j++)
            {
                if(j % 2 == 1){
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-1] - prices[i]);  //买入
                }else{
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-1] + prices[i]);    //卖出
                }
 
            }
 
        }
 
        return dp[len-1][2*k];
    }
};

最佳买卖股票时机含冷冻期

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
 
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
示例 1:
 
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
 
输入: prices = [1]
输出: 0

 
/*
* @lc app=leetcode.cn id=309 lang=cpp
*
* [309] 最佳买卖股票时机含冷冻期
*/
// @lc code=start
#include <vector>
#include <algorithm>
using namespace std;
class Solution
{
    /*
dp[i][0] 买入状态：
1.前一天
2.保持卖出的状态 - 今天金额
3.冷冻期  - 今天金额
dp[i][1] 保持卖出状态
1.前一天保持卖出
2.前一天冷冻期
dp[i][2] 今天卖出
1.前一天持有  + 今天金额
dp[i][3] 冷冻状态
1.前一天卖出
*/
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(4, 0));
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++)
        {
            dp[i][0] = max(dp[i-1][0],max(dp[i-1][1] - prices[i],dp[i-1][3]- prices[i]));
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][3] = dp[i - 1][2];
        }
        int result = max(dp[n - 1][1], max(dp[n - 1][2], dp[n - 1][3]));
        return result;
    }
};
// @lc code=end

买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。
 
你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
 
返回获得利润的最大值。
 
注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
 
示例 1：
 
输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2：
 
输入：prices = [1,3,7,5,10,3], fee = 3
输出：6

 
/*
* @lc app=leetcode.cn id=714 lang=cpp
*
* [714] 买卖股票的最佳时机含手续费
*/
// @lc code=start
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2, 0));
        dp[0][0] = -prices[0];
        for (int i = 1; i < n; i++)
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]  - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - fee + prices[i]);
        }
        return dp[n - 1][1];
    }
};
// @lc code=end

广度优先搜索

说的是二叉树的层次遍历，在C++里面主要使用队列实现，利用先入先出规则，来保留每一层的信息

剑指 Offer 32 - I. 从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。
 
 
 
例如:
给定二叉树: [3,9,20,null,null,15,7],
 
    3
   / \
  9  20
    /  \
   15   7
返回：
 
[3,9,20,15,7]

/**
* Definition for a binary tree node.
* struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int> vec;
        if (root == NULL) { // 初始判空处理
            return vec;
        }
 
        queue<TreeNode*> que; // 创建队列
        que.push(root); // 加入根节点
 
        while (!que.empty()) { // 循环队列不为空
            TreeNode* temp = que.front(); // 队首
            que.pop(); // 弹出队首
            if (temp->left) { // 不为空就入队
                que.push(temp->left);
            }
            if (temp->right) {
                que.push(temp->right);
            }
            vec.push_back(temp->val);
        }
        return vec;
    }
};

102. 二叉树的层序遍历 - 力扣（LeetCode）

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。
 
 
示例 1：
 
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]
示例 2：
 
输入：root = [1]
输出：[[1]]
示例 3：
 
输入：root = []
输出：[]

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

参考资料：

二叉树的层次遍历（C++）_二叉树层序遍历c++_海螺蜜的博客-CSDN博客

回溯算法

定义

就是暴力搜索

回溯法解决的问题

组合问题
切割问题
子集问题
排列问题
棋盘问题

如何理解回溯问题

每个回溯都可以抽象成为一个树形结构，递归深度就是树的深度，

回溯模板

void backtracking(参数){
if（终止条件）
收集结果
return 结果
 
//单层搜索逻辑
for（遍历集合的元素)
处理相关的节点
递归函数
回溯操作
return 操作
}

每一层递归都是一层for循环

回溯具体问题

leetcode 77题组合问题

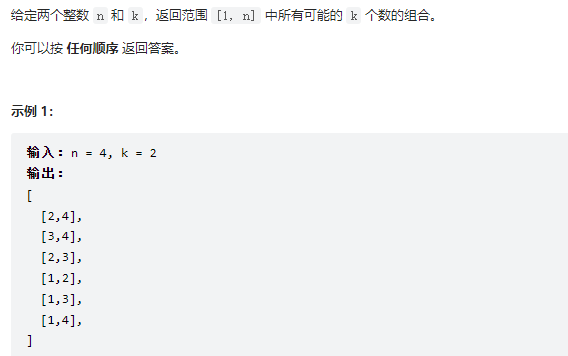
递归三部曲

递归函数的参数以及返回值
确定终止条件
单层递归逻辑

class Solution {
private:
    vector<vector<int>> result; // 存放符合条件结果的集合
    vector<int> path; // 用来存放符合条件结果
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1); // 递归
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear(); // 可以不写
        path.clear();   // 可以不写
        backtracking(n, k, 1);
        return result;
    }
};

KMP算法学习

作用

KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

前缀表

next数组

写过KMP的同学，一定都写过next数组，那么这个next数组究竟是个啥呢？

next数组就是一个前缀表（prefix table）。

前缀表有什么作用呢？

前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

为了清楚的了解前缀表的来历，我们来举一个例子：

要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

最长公共前后缀

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

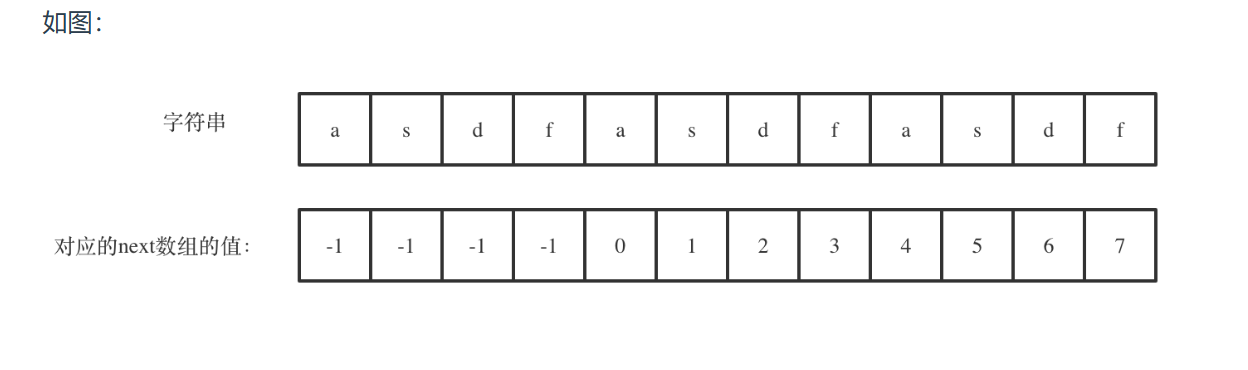
计算前缀表

初始化
处理前后缀不相同的情况
处理前后缀相同的情况
更新next数组的值

j是前缀末尾的位置。i是后缀末尾的位置

void getNext(int* next, const string& s){
    //初始化
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同
            j = next[j]; // 向前回退
        }
        if (s[i] == s[j + 1]) { // 相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
}

使用next数组来做匹配

int strStr(string haystack, string needle) {
        if (needle.size() == 0) { //长度为0的时候
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = -1; // // 因为next数组里记录的起始位置为-1
        for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
            while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
                j++; // i的增加在for循环里
            }
            if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
                return (i - needle.size() + 1); //返回第一个下标
            }
        }

动态规划学习

定义

动态规划与分治方法类似，都是通过组合子问题的解来来求解原问题的。再来了解一下什么是分治方法，以及这两者之间的差别，分治方法将问题划分为互不相交的子问题，递归的求解子问题，再将它们的解组合起来，求出原问题的解。而动态规划与之相反，动态规划应用与子问题重叠的情况，即不同的子问题具有公共的子子问题（子问题的求解是递归进行的，将其划分为更小的子子问题）。在这种情况下，分治方法会做许多不必要的工作，他会反复求解那些公共子子问题。而动态规划对于每一个子子问题只求解一次，将其解保存在一个表格里面，从而无需每次求解一个子子问题时都重新计算，避免了不必要的计算工作。

注意

一般需要在给定约束条件下优化某种指标时候采用动态规划
大问题可以分解成为彼此独立且离散的子问题
自己建立相关的网格
一行一行的优化网格中的数值，单元格中的值就是要优化的值
每个网格都是一个子问题
每个问题都是确定的，yes or no 否则不可以使用动态规划，但是可以使用贪心算法

一般的步骤：

分阶段，将原问题划分成几个子问题。一个子问题就是多轮决策的一个阶段，它们可以是不满足独立性的。
找状态，选择合适的状态变量 Sk。它需要具备描述多轮决策过程的演变，更像是决策可能的结果。
做决策，确定决策变量 uk。每一轮的决策就是每一轮可能的决策动作，例如 D2 的可能的决策动作是 D2 -> E2 和 D2 ->E3。
状态转移方程。这个步骤是动态规划最重要的核心，即 sk+1= uk(sk) 。
定目标。写出代表多轮决策目标的指标函数 Vk,n。
寻找终止条件。

和贪心算法的区别

动规是由前一个状态推导出来的，而贪心是局部直接选最优的，

具体步骤：

对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

狄克斯特拉算法

作用：找到加权图中前往终点的最短路径（非加权图用广度优先搜索）

算法计算步骤

找出最便宜的节点，即可以在最短时间内达到的节点
对该节点的邻居节点，检查是否有前往他们的更短路径，如果有，更新开销列表
对每个节点重复这个过程
计算最终路径（找出每个节点的父节点）

注意点

如果想要获得路径，需要建立两个表，一个父节点表，一个距离表格
权重不能出现负数，出现负数需要使用——贝尔曼-福德算法
该加权图中不能有环

C++实现排序算法

排序算法总结

重要的算法：插入排序堆排序归并排序快速排序

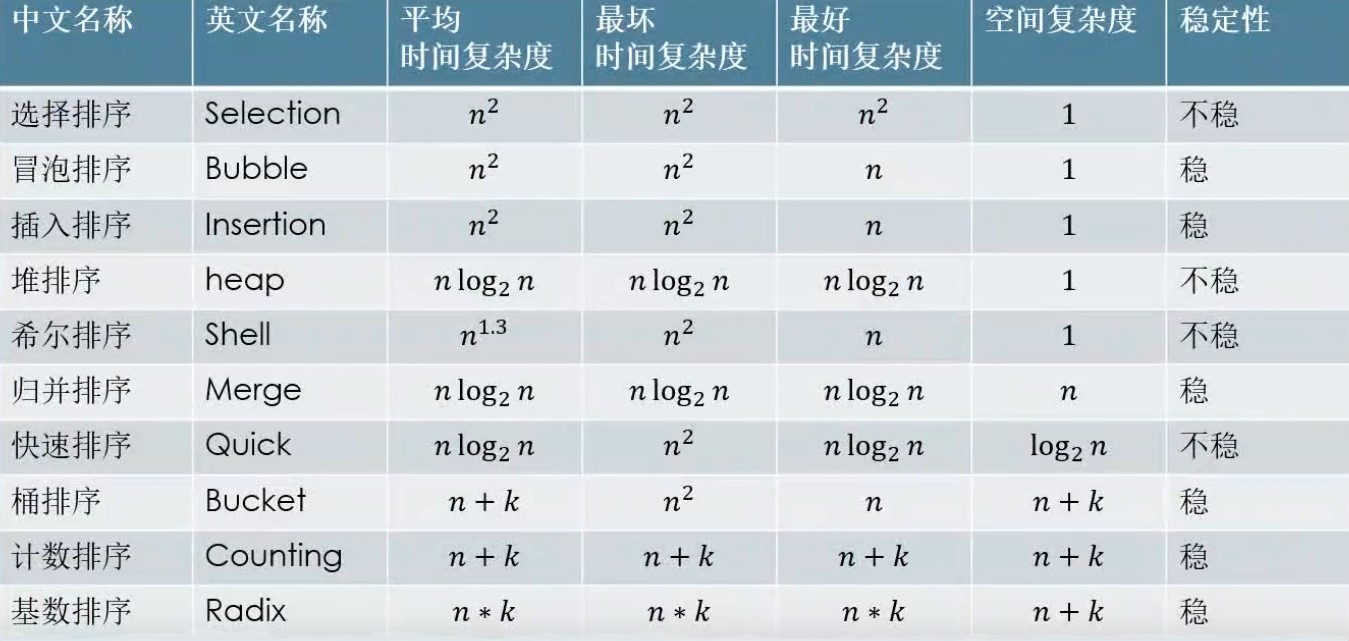
排序的稳定性

当数值一样的时候，原来在前面的还是在前面，原来在后面的是在后面

冒泡排序

现在输入 10 个用户的有效学习时间，要求对它们按由小到大的顺序排序。

解题思路：这种问题是一个典型的排序问题，排序方法是一种重要且基本的算法，我们在此使用“冒泡排序法”，其思路为：每次将相邻两个数比较，将小的调到前面，如果有 6 个数：8，7，5，4，2，0。第一次先将最前面的两个数 8 和 7 对调（看下图）。第二次将第二个数和第三个数（8 和 5）对调。如此总计进行了 5 次，得到 7-5-4-2-0-8 的顺序，可以看到：最大的数 8 已经沉底，成为最下面的一个数，而小的数上升。经过第一轮（5 次比较）后，得到了最大的数 8。

冒泡排序图解：

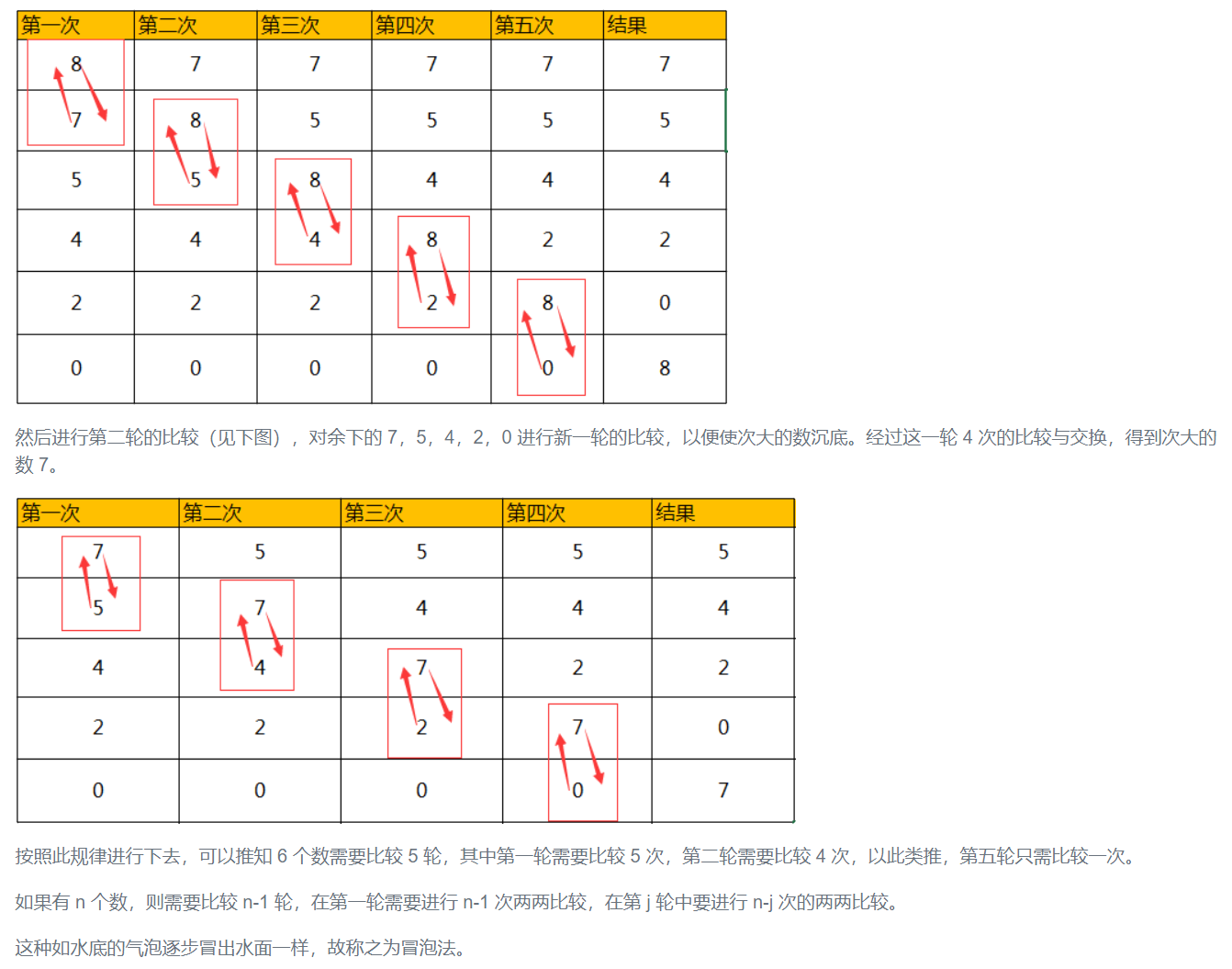
简单总结：

如果有 n 个数，则需要比较 n-1 轮，在第一轮需要进行 n-1 次两两比较，在第 j 轮中要进行 n-j 次的两两比较。

这种如水底的气泡逐步冒出水面一样，故称之为冒泡法。

例题：

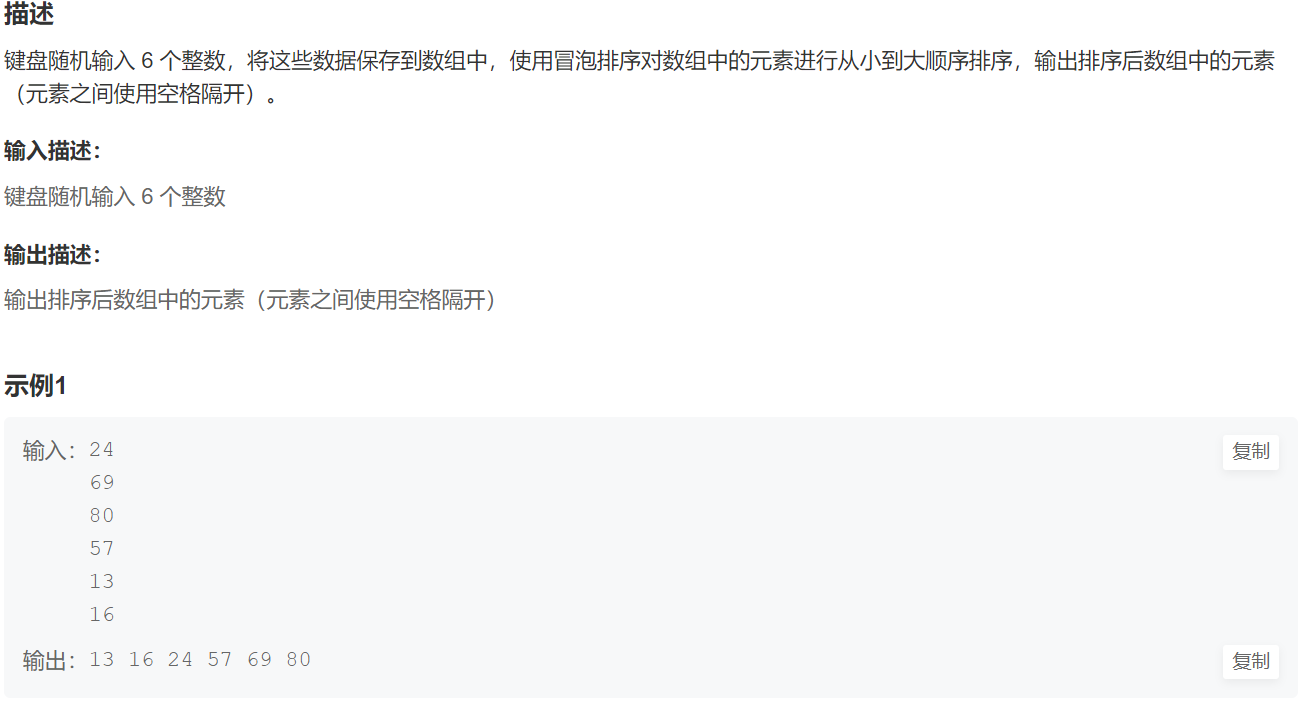
#include <iostream>
using namespace std;
void swap(int &a, int  &b) {
    int temp;
    temp = a;
    a = b;
    b = temp; }
int main() {
    int arr[6] = { 0 };
    int len = sizeof(arr) / sizeof(int);
    for (int i = 0; i < len; i++) { cin >> arr[i]; }
    // write your code here......
    for (int i = 0; i < len-1; i++) {
        for (int j = 0; j < len-i-1; j++) {
            if (arr[j]>arr[j+1]) {
                swap(arr[j], arr[j+1]);
            }
        }
    }
    for (int i = 0; i < len; i++) {
        cout << arr[i] << " ";  }
    return 0;
}

核心代码：

for (int i = 0; i < len-1; i++)
{
    for (int j = 0; j < len-i-1; j++)
    {
        if (arr[j]>arr[j+1])
        {
            swap(arr[j], arr[j+1]);
        }
    }
}

方法二：

for (int i = 0; i < len -1; i++)
    {
        for (int j = len - 2; j >= i; j--)
        {
            if (arr[j] > arr[j+1])
            {
                swap(arr[j], arr[j + 1]);
            }
        }
    }

for 循环的书写方法左开右闭几个数就是几

//for (int q = 0; q < 10; q++) //十个数第二个Q后面是10

1//for (int q = 0; q < 10; q++) //十个数第二个Q后面是10

选择排序

简单的打擂台，选定第一个为最小，然后后面一直更新最小的下标，最后如果不得，进行交换，相当于一个一个把最小的交换到前面去。

for (int i = 0; i < len; i++)  //len-1也可行
    {
        int min = i;
        for (int j = i+1; j < len; j++)
        {
            if (arr[j] < arr[min])
            {
                min = j;
            }
        }
        if (min != i)
        {
            swap(arr[min], arr[i]);
        }
    }

插入排序算法：

相当于打扑克摆拍。第一个已经拍好了，剩下的排列在前面或者后面，根据情况具体分析

简单来说，如果小就提前，如果大就不操作

//插入排序
    for (int i = 1; i < len; i++)  //第一个已经排好顺序
    {
        int j;
        if (arr[i] < arr[i-1])
        {
            int tmp = arr[i];
            for (j = i-1; arr[j] > tmp && j >= 0;j--)  //改成while代码
            {
                arr[j + 1] = arr[j];
            }
 
            arr[j + 1] = tmp;
        }
    }

while 代码：

for (int i = 1; i < len ; i++)
    {
        int j = i - 1;
        if (arr[i] < arr[i-1])
        {
            int tmp = arr[i];
            while (arr[j] > tmp && j >=0)
            {
                arr[j + 1] = arr[j];
                j--;
            }
            arr[j + 1] = tmp;
        }
    }

void InsertSort(int *arr,int length)//直接插入排序
{
    int i,j;
    for(i = 2;i<=length;i++)//从第二个数字开始比较，一个数字是有序的不需要比较
    {
        if(arr[i]<arr[i-1])//如果说，要排序的数字比前面的数小，则进行下面的操作，否则啥也不干
        {
            arr[0]=arr[i];//下标0，用作哨兵，放要排序的数字
 
        for(j = i-1;arr[0]<arr[j];j--)//在排序的数字小于排序位置之前的数字时，就不断把大数往后移动
        {
            arr[j+1]=arr[j];
        }
        arr[j+1]=arr[0];//注意此时的位置必须为j+1，因为在for循环中先减少的j，才去判断。我们要在这里补回多减去的1
        }
    }
}

插排的步骤总结

后一个比前一个小
j定义为上一个 j = i - 1;
循环赋值，知道大于或者小于0

希尔排序

希尔排序就是加了一个增量的插入排序

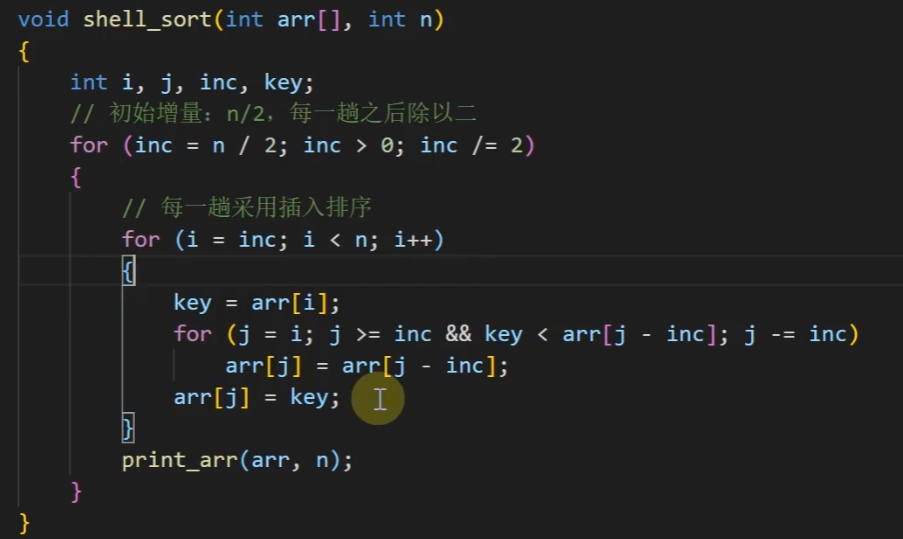
int inc = len ;
    while (inc > 1 )
    {
        inc = inc / 3 + 1;
        for (int i = inc ; i <len; i++)
        {
            if (arr[i] < arr[i-inc])
            {
                int tmp = arr[i];
                int j;
                for ( j = i - inc;  j >=0 && tmp < arr[j]; j-=inc)
                {
                    arr[j+inc] = arr[j];
                }
                arr[j+inc] = tmp;
            }
        }
    }

堆排序

大顶堆的知识点：

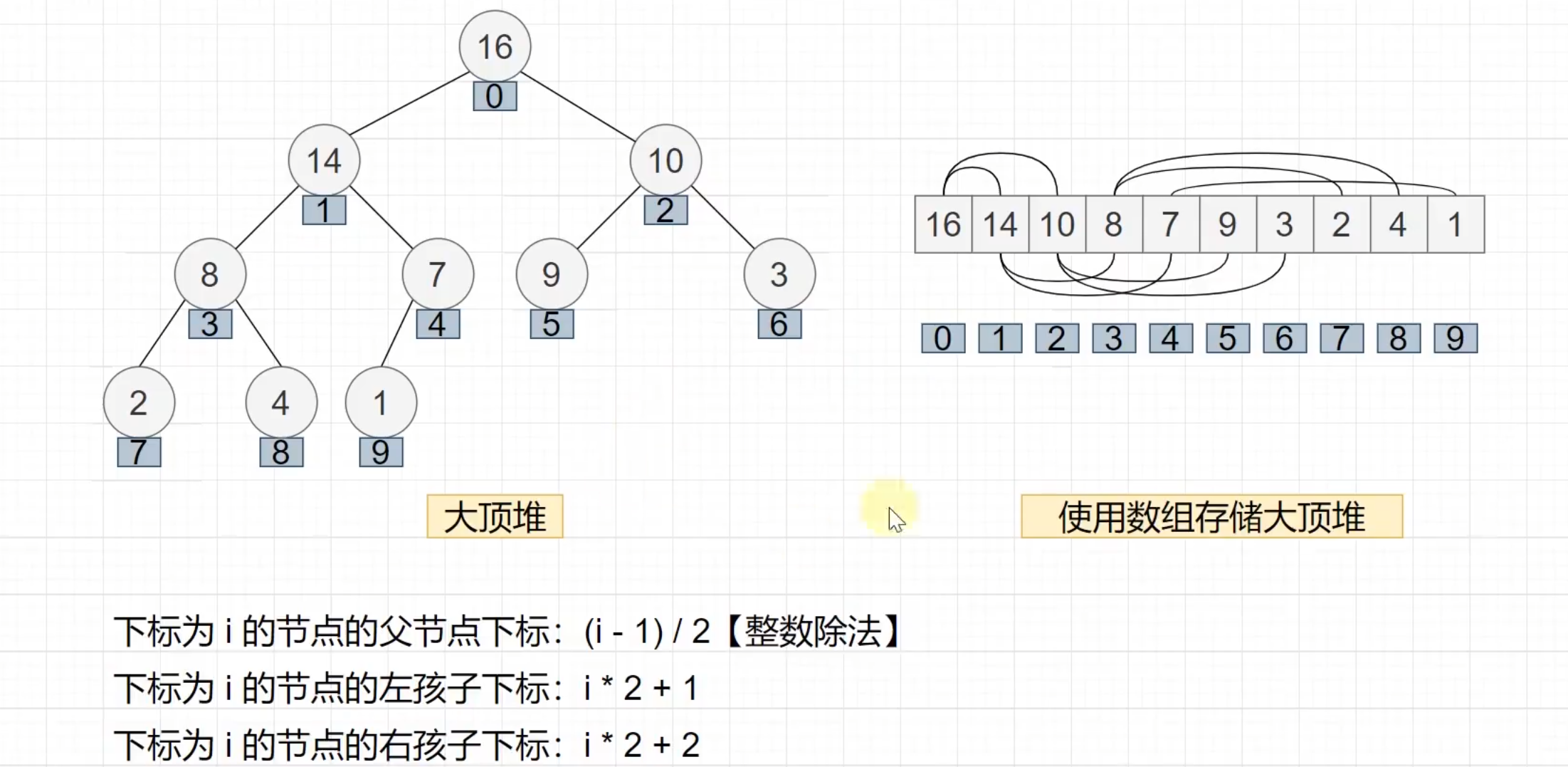
堆维护代码：

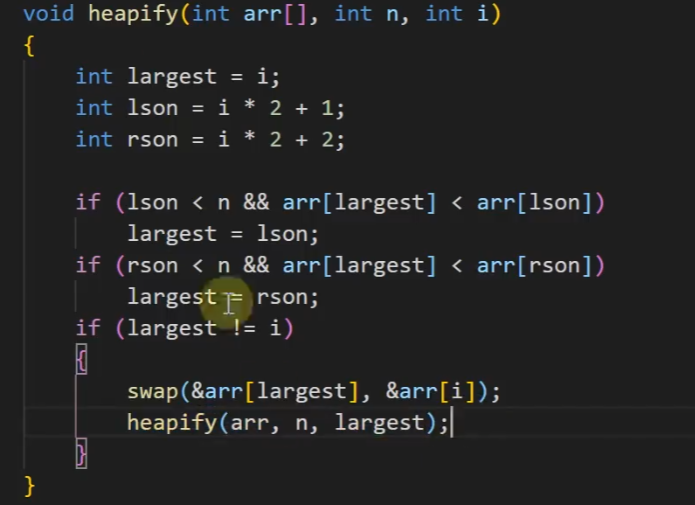
建堆代码：

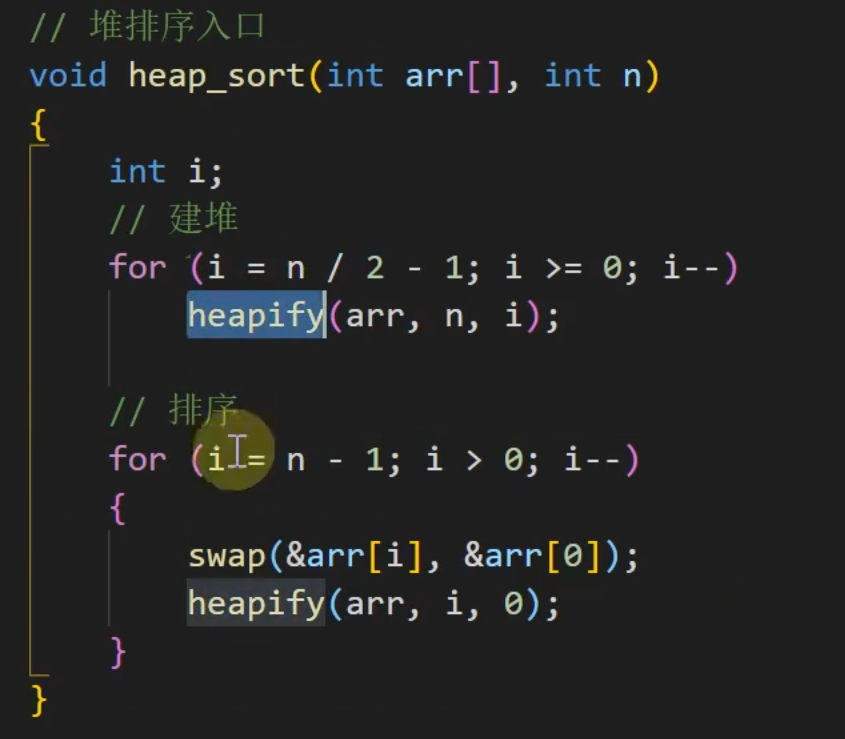
除以2是因为根节点必须是上面的，如图所示，只需要一半就可以维护堆

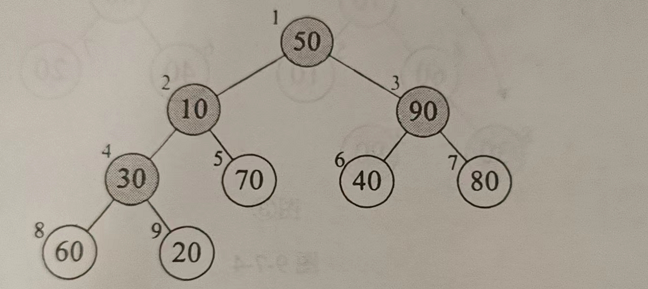
因为是排序，把最大的放在最后面，所以使用大顶堆，把数值最大的放在最前面与后面的交换，得到有正确排序的数组

//1.堆维护
void heapify(int a[], int n, int i) {
    int largest = i;
    int lson = i * 2 + 1;
    int rson = i * 2 + 2;
 
    if (lson < n && a[largest] < a[lson])
    {
        largest = lson;
    }
    if (rson < n && a[largest] < a[rson])
    {
        largest = rson;
    }
 
    if (largest != i)
    {
        my_swap(a[largest], a[i]);
        heapify(a, n, largest);
    }
}
 
void dui(int a[], int n) {
 
    int i;
    //建堆
    for (int i = n / 2 - 1; i >= 0 ; i--)
    {
        heapify(a, n, i);
    }
 
    //排序
    for (int i = n - 1; i > 0; i--)
    {
        my_swap(a[i], a[0]);
        heapify(a, i, 0);
    }
}

归并排序

总体思路：

先划分再合并，称为归并排序

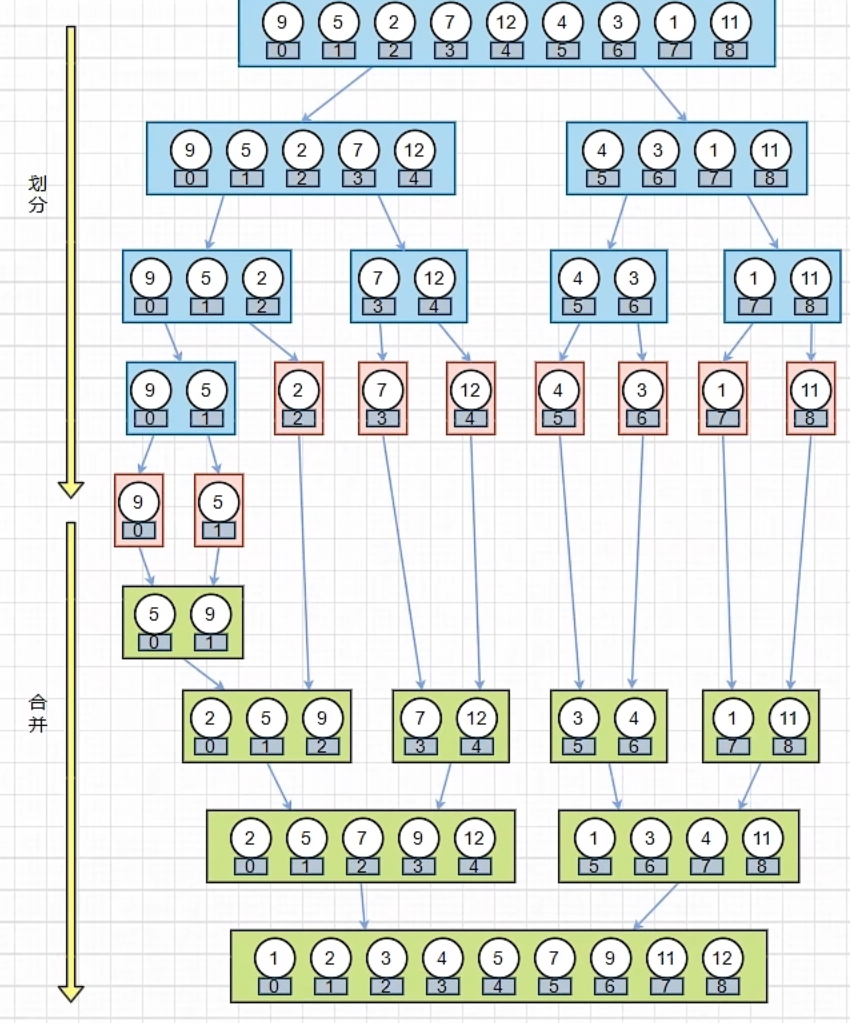
//归并排序
 
//1.合并函数
void merge(int a[],int tempArr[], int left, int mid, int right) {
    //标记左半区第一个未排序的元素
    int l_pos = left;
 
    //标记右半区第一个未排序的元素
    int r_pos = mid + 1;
 
    //临时数组元素的下标
    int pos = left;
 
    //合并
    while (l_pos <= mid && r_pos <= right)
    {
        if (a[l_pos] < a[r_pos]) {
            tempArr[pos++] = a[l_pos++];
        }
        else {
            tempArr[pos++] = a[r_pos++];
        }
    }
 
    //合并左半区剩余的元素
    while (l_pos <= mid)
    {
        tempArr[pos++] = a[l_pos++];
    }
 
    //合并右半区剩余的元素
    while (r_pos <= right)
    {
        tempArr[pos++] = a[r_pos++];
    }
 
    //把临时数组中合并后的元素复制回原来的数组
    while (left <= right)
    {
        a[left] = tempArr[left];
        left++;
    }
}
 
//2.分治函数
void   msort(int a[], int tempArr[], int left, int right) {
 
    if (left < right)
    {
        //find mid
        int mid = (left + right) / 2;
 
        //sort left
        msort(a, tempArr, left, mid);
 
        //sort right
        msort(a, tempArr, mid + 1, right);
 
        merge(a, tempArr, left, mid, right);
    }
 
}
 
//3.归并排序
void guibing(int a[], int n) {
 
    int *tempArr = (int *)malloc(n * sizeof(int));
 
    if (tempArr)
    {
        msort(a, tempArr, 0, n - 1);
        free(tempArr);
    }
    else
    {
        printf("error : failed to allocate memory\n");
    }
}

快速排序算法

使用的是头文件 stdlib.h

用法：

选择排序
选择排序思路，假定一个最小或最大值，根据题意这里假定一个最小值等于arr[0]
调用i后的数组元素的值和假定最小值比较，比最小值还小，互相交换
一轮循环比对过后把最小值赋值给当前i对应的元素，（比如，当前i0,那么arr[0]=min,如果当前i1, 那么arr[1]=min,这个min就是第二小的值，以此类推得到一个从小到大排序的数组）
i的值++，重复进行比较，重写交换和赋值，直到完成

/*******************  快速排序  ************************/
 
//分治
int partition(int a[], int low,int high) {
    int pivot = a[high];
    int i = low;
 
    for (int j = low; j < high; j++)
    {
        if (a[j] < pivot)
        {
            my_swap(a[j], a[i]);
            i++;
        }
    }
    my_swap(a[high], a[i]);
    return i;
}
 
//递归划分
void qsort1(int a[], int low, int high) {
    if (low < high)
    {
        int mid = partition(a, low, high);
        qsort1(a, low, mid - 1);
        qsort1(a, mid + 1, high);
    }
 
}
 
void kuaisu(int a[], int n) {
    qsort1(a, 0, n - 1);
}

全部总代码与部分代码

测试主函数代码

int main() {
 
    int arr[15] = { 11,1,5,6,8,2,56,48,16,23,22,18,14,3,88};
    //int len = sizeof(a) / sizeof(a[0]);
    int len = size(arr);
 
    //origan_show
    printf("原来的数组输出为：\n");
    printf("{");
    for (int i = 0; i < len; i++)
    {
        if (i != len - 1)
        {
            printf("%d,", arr[i]);
        }
        else
        {
            printf("%d", arr[i]);
        }
 
    }
    printf("}\n");
 
    //调用
    // 1.冒泡
    //maopao(arr,len);
 
    // 2.选择
    //xuanze(arr, len);
 
    // 3.插入
    //charu(arr, len);
 
    // 希尔排序
    xier(arr, len);
 
    //堆排序
    dui(arr, len);
 
    //归并排序
    guibing(arr, len);
 
    //快速排序
    kuaisu(arr, len);
 
 
    //result_show
    printf("排序后的数组输出为：\n");
    printf("{");
    for (int i = 0; i < len; i++)
    {
        if (i != len - 1)
        {
            printf("%d,", arr[i]);
        }
        else
        {
            printf("%d", arr[i]);
        }
 
    }
    printf("}\n");
    return 0;
}

前四种排序方法代码

/*********************  冒泡排序 ***********************/
 
//基础交换函数
void my_swap(int &a, int &b) {
    int tmp;
    tmp = a;
    a = b;
    b = tmp;
}
 
//冒泡排序
void maopao(int a[],int n) {
    // circle times
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n - 1 - i; j++)
        {
            if (a[j] >= a[j+1])
            {
                my_swap(a[j], a[j + 1]);
            }
        }
    }
}
 
 
/*********************  选择排序 ***********************/
 
void xuanze(int a[],int n) {
 
    for (int i = 0; i < n - 1; i++)
    {
        int min = i;
        for (int j = i + 1; j < n; j++)
        {
            if (a[j] < a[min])
            {
                min = j;
            }
        }
        my_swap(a[i], a[min]);
    }
}
 
 
 
/*********************  插入排序 ***********************/
 
void charu(int a[], int n) {
    int i = 1;
    while (i < n)
    {
        if (a[i] < a[i-1])
        {
            int j = i - 1;
            int tmp = a[i];
            while (tmp < a[j] && j >= 0)
            {
                a[j + 1] = a[j];
                j--;
            }
            a[j + 1] = tmp;
        }
        i++;
    }
 
}
 
/*********************  希尔排序 ***********************/
 
void xier(int a[], int n) {
    int inc = n;
    while (inc > 1)
    {
        inc = inc / 3 + 1;
        for (int i = inc; i < n; i++)
        {
            if (a[i] < a[i - inc])
            {
                int j = i - inc;
                int tmp = a[i];
                while (tmp < a[j] && j >= 0 )
                {
                    a[j + inc] = a[j];
                    j -= inc;
                }
                a[j + inc] = tmp;
            }
        }
    }
}

后三种排序方法代码

/********************  堆排序  ************************/
 
 
//1.堆维护
void heapify(int a[], int n, int i) {
    int largest = i;
    int lson = i * 2 + 1;
    int rson = i * 2 + 2;
 
    if (lson < n && a[largest] < a[lson])
    {
        largest = lson;
    }
    if (rson < n && a[largest] < a[rson])
    {
        largest = rson;
    }
 
    if (largest != i)
    {
        my_swap(a[largest], a[i]);
        heapify(a, n, largest);
    }
}
 
void dui(int a[], int n) {
 
    int i;
    //建堆
    for (int i = n / 2 - 1; i >= 0 ; i--)
    {
        heapify(a, n, i);
    }
 
    //排序
    for (int i = n - 1; i > 0; i--)
    {
        my_swap(a[i], a[0]);
        heapify(a, i, 0);
    }
}
 
/*******************  归并排序  ************************/
 
//1.合并函数
void merge(int a[],int tempArr[], int left, int mid, int right) {
    //标记左半区第一个未排序的元素
    int l_pos = left;
 
    //标记右半区第一个未排序的元素
    int r_pos = mid + 1;
 
    //临时数组元素的下标
    int pos = left;
 
    //合并
    while (l_pos <= mid && r_pos <= right)
    {
        if (a[l_pos] < a[r_pos]) {
            tempArr[pos++] = a[l_pos++];
        }
        else {
            tempArr[pos++] = a[r_pos++];
        }
    }
 
    //合并左半区剩余的元素
    while (l_pos <= mid)
    {
        tempArr[pos++] = a[l_pos++];
    }
 
    //合并右半区剩余的元素
    while (r_pos <= right)
    {
        tempArr[pos++] = a[r_pos++];
    }
 
    //把临时数组中合并后的元素复制回原来的数组
    while (left <= right)
    {
        a[left] = tempArr[left];
        left++;
    }
}
 
//2.分治函数
void   msort(int a[], int tempArr[], int left, int right) {
 
    if (left < right)
    {
        //find mid
        int mid = (left + right) / 2;
 
        //sort left
        msort(a, tempArr, left, mid);
 
        //sort right
        msort(a, tempArr, mid + 1, right);
 
        merge(a, tempArr, left, mid, right);
    }
 
}
 
//3.归并排序
void guibing(int a[], int n) {
 
    int *tempArr = (int *)malloc(n * sizeof(int));
 
    if (tempArr)
    {
        msort(a, tempArr, 0, n - 1);
        free(tempArr);
    }
    else
    {
        printf("error : failed to allocate memory\n");
    }
}
 
 
/*******************  快速排序  ************************/
 
//分治
int partition(int a[], int low,int high) {
    int pivot = a[high];
    int i = low;
 
    for (int j = low; j < high; j++)
    {
        if (a[j] < pivot)
        {
            my_swap(a[j], a[i]);
            i++;
        }
    }
    my_swap(a[high], a[i]);
    return i;
}
 
//递归划分
void qsort1(int a[], int low, int high) {
    if (low < high)
    {
        int mid = partition(a, low, high);
        qsort1(a, low, mid - 1);
        qsort1(a, mid + 1, high);
    }
 
}
 
void kuaisu(int a[], int n) {
    qsort1(a, 0, n - 1);
}

最后的总程序

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;
 
 
 
/*********************  冒泡排序 ***********************/
 
//基础交换函数
void my_swap(int &a, int &b) {
    int tmp;
    tmp = a;
    a = b;
    b = tmp;
}
 
//冒泡排序
void maopao(int a[], int n) {
    // circle times
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = 0; j < n - 1 - i; j++)
        {
            if (a[j] >= a[j + 1])
            {
                my_swap(a[j], a[j + 1]);
            }
        }
    }
}
 
 
/*********************  选择排序 ***********************/
 
void xuanze(int a[], int n) {
 
    for (int i = 0; i < n - 1; i++)
    {
        int min = i;
        for (int j = i + 1; j < n; j++)
        {
            if (a[j] < a[min])
            {
                min = j;
            }
        }
        my_swap(a[i], a[min]);
    }
}
 
 
 
/*********************  插入排序 ***********************/
 
void charu(int a[], int n) {
    int i = 1;
    while (i < n)
    {
        if (a[i] < a[i - 1])
        {
            int j = i - 1;
            int tmp = a[i];
            while (tmp < a[j] && j >= 0)
            {
                a[j + 1] = a[j];
                j--;
            }
            a[j + 1] = tmp;
        }
        i++;
    }
 
}
 
/*********************  希尔排序 ***********************/
 
void xier(int a[], int n) {
    int inc = n;
    while (inc > 1)
    {
        inc = inc / 3 + 1;
        for (int i = inc; i < n; i++)
        {
            if (a[i] < a[i - inc])
            {
                int j = i - inc;
                int tmp = a[i];
                while (tmp < a[j] && j >= 0)
                {
                    a[j + inc] = a[j];
                    j -= inc;
                }
                a[j + inc] = tmp;
            }
        }
    }
}
 
 
/********************  堆排序  ************************/
 
 
//1.堆维护
void heapify(int a[], int n, int i) {
    int largest = i;
    int lson = i * 2 + 1;
    int rson = i * 2 + 2;
 
    if (lson < n && a[largest] < a[lson])
    {
        largest = lson;
    }
    if (rson < n && a[largest] < a[rson])
    {
        largest = rson;
    }
 
    if (largest != i)
    {
        my_swap(a[largest], a[i]);
        heapify(a, n, largest);
    }
}
 
void dui(int a[], int n) {
 
    int i;
    //建堆
    for (int i = n / 2 - 1; i >= 0; i--)
    {
        heapify(a, n, i);
    }
 
    //排序
    for (int i = n - 1; i > 0; i--)
    {
        my_swap(a[i], a[0]);
        heapify(a, i, 0);
    }
}
 
/*******************  归并排序  ************************/
 
//1.合并函数
void merge(int a[], int tempArr[], int left, int mid, int right) {
    //标记左半区第一个未排序的元素
    int l_pos = left;
 
    //标记右半区第一个未排序的元素
    int r_pos = mid + 1;
 
    //临时数组元素的下标
    int pos = left;
 
    //合并
    while (l_pos <= mid && r_pos <= right)
    {
        if (a[l_pos] < a[r_pos]) {
            tempArr[pos++] = a[l_pos++];
        }
        else {
            tempArr[pos++] = a[r_pos++];
        }
    }
 
    //合并左半区剩余的元素
    while (l_pos <= mid)
    {
        tempArr[pos++] = a[l_pos++];
    }
 
    //合并右半区剩余的元素
    while (r_pos <= right)
    {
        tempArr[pos++] = a[r_pos++];
    }
 
    //把临时数组中合并后的元素复制回原来的数组
    while (left <= right)
    {
        a[left] = tempArr[left];
        left++;
    }
}
 
//2.分治函数
void   msort(int a[], int tempArr[], int left, int right) {
 
    if (left < right)
    {
        //find mid
        int mid = (left + right) / 2;
 
        //sort left
        msort(a, tempArr, left, mid);
 
        //sort right
        msort(a, tempArr, mid + 1, right);
 
        merge(a, tempArr, left, mid, right);
    }
 
}
 
//3.归并排序
void guibing(int a[], int n) {
 
    int *tempArr = (int *)malloc(n * sizeof(int));
 
    if (tempArr)
    {
        msort(a, tempArr, 0, n - 1);
        free(tempArr);
    }
    else
    {
        printf("error : failed to allocate memory\n");
    }
}
 
 
/*******************  快速排序  ************************/
 
//分治
int partition(int a[], int low,int high) {
    int pivot = a[high];
    int i = low;
 
    for (int j = low; j < high; j++)
    {
        if (a[j] < pivot)
        {
            my_swap(a[j], a[i]);
            i++;
        }
    }
    my_swap(a[high], a[i]);
    return i;
}
 
//递归划分
void qsort1(int a[], int low, int high) {
    if (low < high)
    {
        int mid = partition(a, low, high);
        qsort1(a, low, mid - 1);
        qsort1(a, mid + 1, high);
    }
 
}
 
void kuaisu(int a[], int n) {
    qsort1(a, 0, n - 1);
}
 
 
int arr[15] = { 11,1,5,6,8,2,56,48,16,23,22,18,14,3,88 };
 
int main() {
 
 
    //int len = sizeof(a) / sizeof(a[0]);
    int len = size(arr);
 
    //origan_show
    printf("原来的数组输出为：\n");
    printf("{");
    for (int i = 0; i < len; i++)
    {
        if (i != len - 1)
        {
            printf("%d,", arr[i]);
        }
        else
        {
            printf("%d", arr[i]);
        }
 
    }
    printf("}\n");
 
    //调用
    // 1.冒泡
    //maopao(arr,len);
 
    // 2.选择
    //xuanze(arr, len);
 
    // 3.插入
    //charu(arr, len);
 
    // 希尔排序
    //xier(arr, len);
 
    //堆排序
    //dui(arr, len);
 
    //归并排序
    //guibing(arr, len);
 
    //快速排序
    kuaisu(arr, len);
 
 
    //result_show
    printf("排序后的数组输出为：\n");
    printf("{");
    for (int i = 0; i < len; i++)
    {
        if (i != len - 1)
        {
            printf("%d,", arr[i]);
        }
        else
        {
            printf("%d", arr[i]);
        }
 
    }
    printf("}\n");
    return 0;
}

其它小技巧

交换的小技巧

一般来说，交换数组中两个数字的函数如下：

int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;

有一道非常经典的数字交换题目：如何在不引入第三个中间变量的情况下，完成两个数字的交换。

这里可以用到一个数学上的技巧：

arr[j + 1] = arr[j + 1] + arr[j];
arr[j] = arr[j + 1] - arr[j];
arr[j + 1] = arr[j + 1] - arr[j];

除了这种先加后减的写法，还有一种先减后加的写法：

arr[j + 1] = arr[j] - arr[j + 1];
arr[j] = arr[j] - arr[j + 1];
arr[j + 1] = arr[j + 1] + arr[j];

但这两种方式都可能导致数字越界。

更好的方案是通过位运算完成数字交换：

arr[i] = arr[i] ^ arr[j];
arr[j] = arr[j] ^ arr[i];
arr[i] = arr[i] ^ arr[j];

异或运算的三个特性：

0和任何数字异或永远等于该数字，0^4=4
两个相同的数字异或等于0，2^2=0
异或满足交换律和结合律，例如a^b=ba,(a^b)c=a^(bc)

参考资料：

排序算法：插入排序【图解+代码】_哔哩哔哩_bilibili

以上排序方法都有，按照顺序看就好了

posted @ 2024-01-03 16:39 快乐气氛组阿宇阅读(60) 评论(0) 编辑收藏举报

刷新页面返回顶部

C++常见算法总结

堆排序学习

参考资料

股票问题

广度优先搜索

参考资料：

回溯算法

定义

回溯法解决的问题

如何理解回溯问题

回溯模板

回溯具体问题

leetcode 77题 组合问题

KMP算法学习

作用

前缀表

next数组

最长公共前后缀

计算前缀表

使用next数组来做匹配

动态规划学习

定义

注意

和贪心算法的区别

狄克斯特拉算法

算法计算步骤

注意点

C++实现排序算法

排序的稳定性

冒泡排序

冒泡排序图解：

简单总结：

核心代码：

选择排序

插入排序算法：

插排的步骤总结

希尔排序

堆排序

归并排序

快速排序算法

全部总代码与部分代码

测试主函数代码

前四种排序方法代码

后三种排序方法代码

最后的总程序

其它小技巧

交换的小技巧

参考资料：

公告

leetcode 77题组合问题